山东省青岛市莱西市2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-11-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个多项式中，可以分解因式的是（）

A、 $x^{2} + x$ B、 $x^{2} - 4 x + 8$ C、 $x^{2} + 2 y + 1$ D、 $x^{2} - 4 y^{3}$

查看试题解析
2. 在式子 $\frac{a}{5}$ ， $\frac{3}{x + 1}$ ， $\frac{3}{x + y}$ ， $\frac{a^{2}}{a}$ ， $\frac{3}{x + y}$ 中，分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列分式是最简分式的是（）

A、 $\frac{15 b}{5 a}$ B、 $\frac{4 b^{3}}{3 a b}$ C、 $\frac{2 - a}{a - 2}$ D、 $\frac{- a - b}{a - b}$

查看试题解析
4. 计算 $\frac{a + 1}{a + 2} + \frac{1}{a + 2}$ 的结果是（）

A、1 B、 $\frac{2}{a + 2}$ C、 $a + 2$ D、 $\frac{a}{a + 2}$

查看试题解析
5. 下列从左到右的变形是分解因式的是（）

A、 $(x + 4) (x - 4) = x^{2} - 16$ B、 $x^{2} - y^{2} + 2 = (x + y) (x - y) + 2$ C、 $(x - 1) (x - 2) = (x - 2) (x - 1)$ D、 $2 a b - 2 a c = 2 a (b - c)$

查看试题解析
6. 下列计算正确的是（）

A、 $\frac{1}{4 x} - \frac{1}{4 y} = \frac{1}{4 (x - y)}$ B、 $\frac{y}{x} + \frac{y}{z} = \frac{2 y}{x z}$ C、 $\frac{x}{3 y} - \frac{x + 1}{3 y} = \frac{1}{3 y}$ D、 $\frac{1}{x - y} + \frac{1}{y - x} = 0$

查看试题解析
7. 照相机成像应用了一个重要原理，用公式 $\frac{1}{f} = \frac{1}{u} + \frac{1}{v} (v \neq f)$ 表示，其中f表示照相机镜头的焦距，u表示物体到镜头的距离，v表示胶片（像）到镜头的距离．已知f，v，则u＝（）

A、 $\frac{f v}{f - v}$ B、 $\frac{f - v}{f v}$ C、 $\frac{f v}{v - f}$ D、 $\frac{v - f}{f v}$

查看试题解析
8. 某次射击比赛，甲队员的成绩如图，根据此统计图，下列结论中错误的是（）

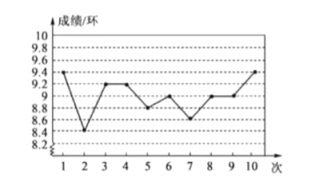A、最高成绩是9.4环 B、平均成绩是9环 C、这组成绩的众数是9环 D、这组成绩的方差是8.7

查看试题解析
9. 如果正数x、y同时扩大10倍，那么下列分式中值保持不变的是（）

A、 $\frac{x - 1}{y - 1}$ B、 $\frac{x + 1}{y + 1}$ C、 $\frac{x^{2}}{y^{3}}$ D、 $\frac{x}{x + y}$

查看试题解析
10. 某班有50人，一次数学测试后，老师对测试成绩进行了统计．由于小颖没有参加此次集体测试，因此计算其他49人的平均分为92分，方差s²＝23．后来小颖进行了补测，成绩是92分，关于该班50人的数学测试成绩，下列说法正确的是（）

A、平均分不变，方差变小 B、平均分不变，方差变大 C、平均分和方差都不变 D、平均分和方差都改变

查看试题解析

二、填空题

11. 因式分解： $x^{2} - 9$ =.

查看试题解析
12. 某品牌专卖店9月份销售了20双运动鞋，其尺码和数量统计如下表：
尺码
38
39
40
41
42
数量
2
4
5
6
3
这20双运动鞋尺码的众数是．

查看试题解析
13. 已知正方形的面积是 $(16 - 8 x + x^{2}) c m^{2} (x > 4)$ ，则正方形的周长是cm．

查看试题解析
14. 学校运动会上，共有15名同学参加了男子100米预赛，参赛选手要想知道自己是否能进入前8名，从而取得决赛资格，只需要了解自己的成绩以及全部成绩的．

查看试题解析
15. 王老师对本班40名学生的血型作了统计，列出如下的统计表，则本班A型血的有人．
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15

查看试题解析
16. 已知 $M = m - 4$ ， $N = m^{2} - 3 m$ ，则M与N的大小关系为MN（填>、<或=）

查看试题解析
17. 如果关于x的方程 $\frac{2 x + m}{x - 1} = 1$ 的解是正数，那么m的取值范围是．

查看试题解析
18. 一个长方形的长与宽分别为a，b，若周长为12，面积为5，则 $a b^{3} + 2 a^{2} b^{2} + a^{3} b$ 的值为．

查看试题解析

三、解答题

19. 分解因式

(1)、 $x^{4} - 8 x^{2} y^{2} + 16 y^{4}$

(2)、 $x^{2} (x + 4) - 4 x (x + 1)$

(3)、 $(x^{2} + 1)^{2} - 4 x^{2}$

(4)、 $x^{2} - 7 x + 12$

查看试题解析
20. 解分式方程

(1)、 $\frac{3 - x}{x - 4} + \frac{1}{4 - x} = 1$

(2)、 $\frac{x + 1}{x - 1} - \frac{4}{x^{2} - 1} = 1$

查看试题解析
21. 化简求值

(1)、先化简，再求值： $(\frac{x}{x + 1} + \frac{1}{x - 1}) \div \frac{1}{x^{2} - 1}$ ，其中 $x = \sqrt{2} - 1$ ．

(2)、先化简，再求值： $\frac{a^{2} - 1}{a^{2} - 2 a + 1} + \frac{2 a - a^{2}}{a - 2} \div a$ 其中a为数据0，-1，-3，1，5的极差．

查看试题解析
22. 某单位欲从内部招聘管理人员一名，对甲、乙、丙三名候选人进行了笔试和面试两项测试，三人的测试成绩如下表所示：

根据录用程序，组织200名职工对三人利用投票推荐的方式进行民主评议，三人得票率（没有弃权票，每位职工只能推荐1人）如上图所示，每得一票记作1分．

(1)、请算出三人的民主评议得分；

(2)、如果根据三项测试的平均成绩确定录用人选，那么谁将被录用（精确到 0.01 )?

(3)、根据实际需要，单位将笔试、面试、民主评议三项测试得分按 4 ： 3 ： 3 的比例确定个人成绩，那么谁将被录用？

查看试题解析
23. 小华想复习分式方程，由于印刷问题，有一个数“？”看不清楚： $\frac{?}{x - 2} + 3 = \frac{1}{2 - x}$ .

(1)、她把这个数“？”猜成5，请你帮小华解这个分式方程；

(2)、小华的妈妈说：“我看到标准答案是：方程的增根是 $x = 2$ ，原分式方程无解”，请你求出原分式方程中“？”代表的数是多少？

查看试题解析
24. ［阅读材料]
下面是某同学对多项式 $(x^{2} - 4 x + 2) (x^{2} - 4 x + 6) + 4$ 进行因式分解的过程．
设 $x^{2} - 4 x = y$
原式= $(y + 2) (y + 6) + 4$ （第一步）
$= y^{2} + 8 y + 16$ （第二步）
$= {(y + 4)}^{2}$ （第三步）
$= (x^{2} - 4 x + 4)^{2}$ （第四步）
请问：

(1)、该同学因式分解的结果是否符合题意？若不符合题意，请直接写出因式分解的最后结果．

(2)、请你模仿以上方法尝试对多项式 $(a^{2} - 2 a) (a^{2} - 2 a + 2) + 1$ 进行因式分解．

查看试题解析
25. 某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同．

(1)、求甲、乙两种树苗每棵的价格各是多少元？

(2)、在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵，此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？

查看试题解析
26. 某校数学社团的小亮、小颖两个同学利用分组分解法进行的因式分解：
小亮： $m^{2} - m n + 2 m - 2 n$
= $(m^{2} - m n) + (2 m - 2 n)$
= $m (m - n) + 2 (m - n)$
= $(m - n) (m + 2)$
小颖： $4 x^{2} - y^{2} - z^{2} + 2 y z$
$= 4 x^{2} - (y^{2} + z^{2} - 2 y z)$
= $2 x^{2} - (y - z)^{2}$
$= (2 x + y - z) (2 x - y + z)$ ．
请你在他们解法的启发下，解决下面问题；

(1)、因式分解 $a^{3} - 3 a^{2} - 9 a + 27$ ；

(2)、因式分解 $x^{2} - 4 x y + 4 y^{2} - 16$ ；

(3)、已知a，b，c是 $Δ A B C$ 的三边，且满足 $a^{2} - a b + c^{2} = 2 a c - b c$ ，判断 $Δ A B C$ 的形状并说明理由．

查看试题解析

尺码	38	39	40	41	42
数量	2	4	5	6	3

组别	A型	B型	AB型	O型
频率	0.4	0.35	0.1	0.15