山东省济南市市中区2022-2023学年八年级上学期期中数学试题
试卷更新日期:2022-11-15 类型:期中考试
一、单选题
-
1. 16的算术平方根是( )A、±8 B、±4 C、4 D、-42. 下列所给出的点中,在第二象限的是( )A、 B、 C、 D、3. 满足下列条件的△ABC不是直角三角形的是( )A、 B、 , , C、 D、4. 在 , , , , , (相邻两个 之间 的个数逐次加 )中,无理数的数是( )个A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 已知点都在直线上,则的大小关系是( )A、 B、 C、 D、7. 已知函数的图象如图所示,则函数的图象大致是( )
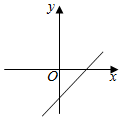 A、
A、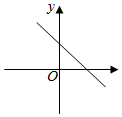 B、
B、 C、
C、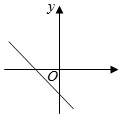 D、
D、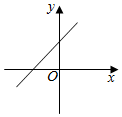 8. 正方体的棱长为2,的中点为M,一只蚂蚁从A点爬行到M点的最短距离为( )
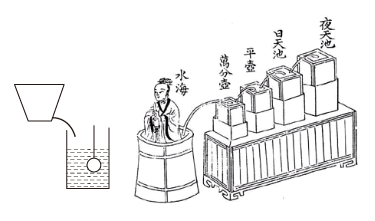
8. 正方体的棱长为2,的中点为M,一只蚂蚁从A点爬行到M点的最短距离为( ) A、 B、 C、5 D、2+9. 漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用,小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,如下表是小明记录的部分数据,其中有一个h的值记录不符合题意,请排除后利用正确的数据确定当时间t为8时,对应的高度h为( )
A、 B、 C、5 D、2+9. 漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用,小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,如下表是小明记录的部分数据,其中有一个h的值记录不符合题意,请排除后利用正确的数据确定当时间t为8时,对应的高度h为( )t(min)
……
0
1
2
3
……
h(cm)
……
0.7
1.2
1.5
1.9
……
 A、3.3 B、3.65 C、3.9 D、4.710. 规定:在平面直角坐标系中,一个点作“0”变换表示将它向右平移一个单位,一个点作“1”变换表示将它关于x轴作对称点,一个点作“2”变换表示将它关于y轴作对称点.由数字0,1,2组成的序列表示一个点按照上面描述依次连续变换.例如:如图,点 按序列“012”作变换,表示点A先向右平移一个单位得到 , 再将关于x轴对称得到 , 再将关于y轴对称得到 ......依次类推.点经过“012012012.......”100次变换后得到点的坐标为( ).(注:“012”算3次变换)
A、3.3 B、3.65 C、3.9 D、4.710. 规定:在平面直角坐标系中,一个点作“0”变换表示将它向右平移一个单位,一个点作“1”变换表示将它关于x轴作对称点,一个点作“2”变换表示将它关于y轴作对称点.由数字0,1,2组成的序列表示一个点按照上面描述依次连续变换.例如:如图,点 按序列“012”作变换,表示点A先向右平移一个单位得到 , 再将关于x轴对称得到 , 再将关于y轴对称得到 ......依次类推.点经过“012012012.......”100次变换后得到点的坐标为( ).(注:“012”算3次变换) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 国庆期间,小强和小明两位同学去电影院看中国外交官撒侨题材电影《万里归途》.在电影票上,小强的“5排4座”记作 , 则小明的“6排7座”可记作 .12. 在平面直角坐标系中,点M(a+1,a﹣1)在x轴上,则a= .13. 如图,是的中线,若 , 则 .
 14. 已知a,b都是实数,若 , 则 .15. 甲、乙两位同学骑自行车,从各自家出发上学,他们离乙家的距离y(km)与出发时间x(min)之间的函数关系如图所示,则乙比甲早到分钟.
14. 已知a,b都是实数,若 , 则 .15. 甲、乙两位同学骑自行车,从各自家出发上学,他们离乙家的距离y(km)与出发时间x(min)之间的函数关系如图所示,则乙比甲早到分钟.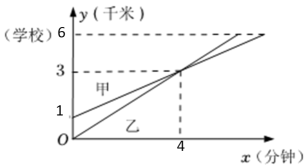 16. 如图,长方形中, , , 点E为射线上一动点(不与D重合),将沿AE折叠得到 , 连接 , 若为直角三角形,则
16. 如图,长方形中, , , 点E为射线上一动点(不与D重合),将沿AE折叠得到 , 连接 , 若为直角三角形,则
三、解答题
-
17. 计算:(1)、(2)、18. 解方程:(1)、;(2)、 .19. 如图,有一架秋千,当它静止时,踏板离地的垂直高度 , 将它往前推送水平距离时,秋千的踏板离地的垂直高度 , 若秋干的绳索始终拉得很直,求绳索的长度.
 20. 在如图所示的方格(每个小正方形的边长为1)中,的顶点A的坐标为 , 顶点C的坐标为 .
20. 在如图所示的方格(每个小正方形的边长为1)中,的顶点A的坐标为 , 顶点C的坐标为 . (1)、在方格图中建立坐标系,并标出原点;(2)、的面积是;(3)、试确定y轴上一点P,使得的和最小,求出的最小值,并画出点P,保留作图痕迹.21. 如图,在四边形中, .
(1)、在方格图中建立坐标系,并标出原点;(2)、的面积是;(3)、试确定y轴上一点P,使得的和最小,求出的最小值,并画出点P,保留作图痕迹.21. 如图,在四边形中, .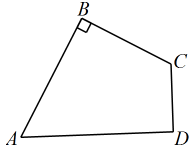 (1)、求证:(2)、求四边形的面积.22. 如图,已知点)、点 .
(1)、求证:(2)、求四边形的面积.22. 如图,已知点)、点 .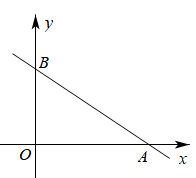 (1)、求直线的函数表达式;(2)、若C为直线上一动点,当的面积为3时,求点C的坐标.23. 冰墩墩是2022年北京冬季奥运会的吉样物.冬奥会来临之际,冰墩墩玩偶非常畅销.小张在某网店选中A,B两款冰墩墩玩偶,决定用900元(全部用完)从该网店进货并销售.两款玩偶的进货价和销售价如下表:
(1)、求直线的函数表达式;(2)、若C为直线上一动点,当的面积为3时,求点C的坐标.23. 冰墩墩是2022年北京冬季奥运会的吉样物.冬奥会来临之际,冰墩墩玩偶非常畅销.小张在某网店选中A,B两款冰墩墩玩偶,决定用900元(全部用完)从该网店进货并销售.两款玩偶的进货价和销售价如下表:A款玩偶
B款玩偶
进货价(元/个)
25
20
销售价(元/个)
33
25
设小张购进A款玩偶x个,B款玩偶y个.
(1)、求y与x之间的函数表达式;(2)、如果小张购进A款玩偶20个,那么这次进货全部售完,能盈利多少元?24. 观察下列一组等式,解答后面的问题:(+1)(-1)=1,
(+)(-)=1,
(+)(-)=1,
(+)(-)=1,
(1)、根据上面的规律:①=;
②=;
(2)、计算:(+++…+)×(+1).(3)、若a= , 则求的值.25. 如图,一次函数与x轴交于点 , 点C在直线上且横坐标为3.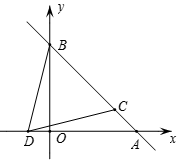 (1)、求k的值和点C的坐标;(2)、点D为x轴上一点, , 求点D的坐标;(3)、在(2)的条件下,若点M是x轴上的动点,问在直线上,是否存在点N(点N与点C不重合),使与全等?若存在,请直接写出点N的坐标,并写出其中一种情况的解答过程,若不存在,请说明理由.26. 综合与实践
(1)、求k的值和点C的坐标;(2)、点D为x轴上一点, , 求点D的坐标;(3)、在(2)的条件下,若点M是x轴上的动点,问在直线上,是否存在点N(点N与点C不重合),使与全等?若存在,请直接写出点N的坐标,并写出其中一种情况的解答过程,若不存在,请说明理由.26. 综合与实践某学校的数学兴趣小组发现这样一个模型,两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,会形成一组全等的三角形,具有这个规律的图形称为“手拉手”图形.
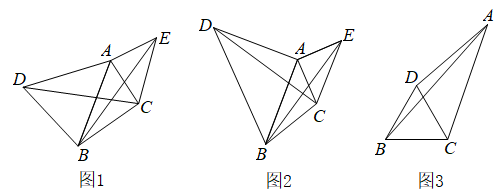 (1)、[材料理解]如图1,在中,分别以 , 为边向外作等腰和等腰 . , , , 连接 , , 试猜想与的大小关系,并说明理由;(2)、[深入探究]如图2,在中, , , , 分别以 , 为边向外作等腰直角和等腰直角 , , 连接 , , 求的长.(3)、[延伸应用]如图3,在中, , 点D为平面内一点,连接 , , 满足 , , , , 求的长.
(1)、[材料理解]如图1,在中,分别以 , 为边向外作等腰和等腰 . , , , 连接 , , 试猜想与的大小关系,并说明理由;(2)、[深入探究]如图2,在中, , , , 分别以 , 为边向外作等腰直角和等腰直角 , , 连接 , , 求的长.(3)、[延伸应用]如图3,在中, , 点D为平面内一点,连接 , , 满足 , , , , 求的长.