山东省滨州市博兴县2022-2023学年八年级上学期期中数学试题
试卷更新日期:2022-11-15 类型:期中考试
一、单选题
-
1. 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 打喷嚏 捂口鼻
B、
打喷嚏 捂口鼻
B、 勤洗手 勤通风
C、
勤洗手 勤通风
C、 戴口罩 讲卫生
D、
戴口罩 讲卫生
D、 喷嚏后 慎揉眼
2. 如果是关于x和y的二元一次方程的解,那么m的值是( )A、 B、4 C、 D、23. 在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )A、1 B、2 C、3 D、44. 已知 ,则a+2b的值是( )A、4 B、6 C、8 D、105. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
喷嚏后 慎揉眼
2. 如果是关于x和y的二元一次方程的解,那么m的值是( )A、 B、4 C、 D、23. 在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )A、1 B、2 C、3 D、44. 已知 ,则a+2b的值是( )A、4 B、6 C、8 D、105. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
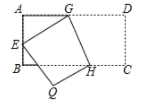 A、112° B、110° C、108° D、106°6. 如图, ≌ ,若 , ,则 的长度为( )
A、112° B、110° C、108° D、106°6. 如图, ≌ ,若 , ,则 的长度为( ) A、4 B、 C、10 D、7. 某市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收2.6元(不足1千米按1千米计),某人从甲地到乙地经过的路程是x千米,出租车费为21元,那么x的最大值是( )A、11 B、8 C、7 D、58. 为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A、4 B、 C、10 D、7. 某市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收2.6元(不足1千米按1千米计),某人从甲地到乙地经过的路程是x千米,出租车费为21元,那么x的最大值是( )A、11 B、8 C、7 D、58. 为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )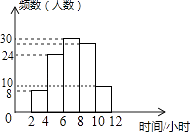 A、280 B、240 C、300 D、2609. 如果等腰三角形一腰上的高与另一腰的夹角为45°,那么这个等腰三角形的底角为( )A、22°50′ B、67.5° C、22°50′或67°50′ D、22.5°或67.5°10. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A、280 B、240 C、300 D、2609. 如果等腰三角形一腰上的高与另一腰的夹角为45°,那么这个等腰三角形的底角为( )A、22°50′ B、67.5° C、22°50′或67°50′ D、22.5°或67.5°10. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )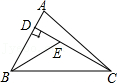 A、10 B、7 C、5 D、411. 如图,在中,分别以点A和点C为圆心,以大于的长为半径作弧,两弧相交于M、N两点;作直线分别交、于点D、E.若cm,的周长为26cm,那么的周长为( )
A、10 B、7 C、5 D、411. 如图,在中,分别以点A和点C为圆心,以大于的长为半径作弧,两弧相交于M、N两点;作直线分别交、于点D、E.若cm,的周长为26cm,那么的周长为( ) A、32cm B、38cm C、44cm D、50cm12. 如图,在和中, . 连接AC,BD交于点M,连接OM.则下列结论:①;②;③平分;④平分 . 其中正确结论的个数为( )
A、32cm B、38cm C、44cm D、50cm12. 如图,在和中, . 连接AC,BD交于点M,连接OM.则下列结论:①;②;③平分;④平分 . 其中正确结论的个数为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 三角形的三边长分别为5,8, ,则x的取值范围是.14. 关于x的不等式组 的所有整数解的积是.15. 用直尺和圆规作一个角等于已知角的示意图如图所示,要证明∠A'O'B'=∠AOB,就要先证明△C’O’D’≌△COD,那么判定△C’O’D’≌△COD的依据是.
 16. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且 , 则 .
16. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且 , 则 .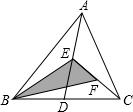 17. 如图,在等边中,D是的中点,于点E,于点F.已知 , 则的长为 .
17. 如图,在等边中,D是的中点,于点E,于点F.已知 , 则的长为 . 18. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为 .
18. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为 .
三、解答题
-
19. 根据要求解答下列各题.(1)、计算:;(2)、解方程组:20. 一个多边形的内角和比其外角和的3倍多180°,求这个多边形的边数.21. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.

( 1 )在图中画出与关于直线l成轴对称的;
( 2 )的面积为多少?
( 3 )在直线l上找一点P,使的长最短.(保留作图痕迹,并写出简单作法)
22. 如图,在△ABC中,点D是BC上一点,且AD=AB, , ∠BAD=∠CAE,连接DE交AC于点F. (1)、若∠B=70°,求∠C的度数:(2)、若AE=AC.求证:AD平分∠BDE.23. 我国传统数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊五,直金十六两.问牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值19两银子;2头牛、5只羊,值16两银子,问每头牛、每只羊分别值银子多少两?”
(1)、若∠B=70°,求∠C的度数:(2)、若AE=AC.求证:AD平分∠BDE.23. 我国传统数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊五,直金十六两.问牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值19两银子;2头牛、5只羊,值16两银子,问每头牛、每只羊分别值银子多少两?”根据以上译文,提出以下两个问题:
(1)、求每头牛、每只羊各值多少两银子?(2)、若某商人准备用19两银子买牛和羊(要求既有牛也有羊,且银两须全部用完),请问商人有几种购买方法?列出所有的可能.24. 如图,在中, . 点D在线段BC上(点D不与点B、C重合),连接AD,作且边DE交线段AC于E. (1)、求证;(2)、若 , 求此时的大小.
(1)、求证;(2)、若 , 求此时的大小.