辽宁省鞍山市铁东区2022-2023学年八年级上学期期中数学试题
试卷更新日期:2022-11-15 类型:期中考试
一、单选题
-
1. 下面是沈阳、大连、青岛、济南四个城市的地铁图标,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 请你量一量如图中边上的高的长度,下列最接近的是( )
2. 请你量一量如图中边上的高的长度,下列最接近的是( )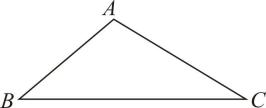 A、 B、 C、 D、3. 已知一个三角形的两边长分别为7和3,则这个三角形的第三边长可能是( )A、3 B、4 C、9 D、124. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )
A、 B、 C、 D、3. 已知一个三角形的两边长分别为7和3,则这个三角形的第三边长可能是( )A、3 B、4 C、9 D、124. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )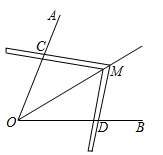 A、 B、 C、 D、5. 如图, , 若 , , 则下列说法正确的是( )
A、 B、 C、 D、5. 如图, , 若 , , 则下列说法正确的是( ) A、 B、 C、 D、6. 下列尺规作图,能确定AD=BD的是( )A、
A、 B、 C、 D、6. 下列尺规作图,能确定AD=BD的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,将直尺和三角板按如图的样子叠放在一起,则( )
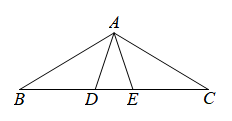
7. 如图,将直尺和三角板按如图的样子叠放在一起,则( ) A、 B、 C、 D、8. 如图,在中,点D,E在边上, , 则添加下列条件后,能证明的有( )
A、 B、 C、 D、8. 如图,在中,点D,E在边上, , 则添加下列条件后,能证明的有( )① ② ③ ④
 A、① B、①② C、①②③ D、①③④
A、① B、①② C、①②③ D、①③④二、填空题
-
9. 如图,为使人字梯更为巩固,在梯子中间安装一个横向“拉杆”,所根据的数学原理是 .
 10. 一个n边形的每个外角都是60°,则这个n边形的内角和是 .11. 如果一个等腰三角形的两边长分别是2和4,那么它的底边长是.12. 如图,是的外角的平分线,若 , , 则的度数是.
10. 一个n边形的每个外角都是60°,则这个n边形的内角和是 .11. 如果一个等腰三角形的两边长分别是2和4,那么它的底边长是.12. 如图,是的外角的平分线,若 , , 则的度数是.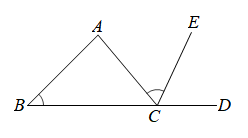 13. 如图,平分 , 于点C,且 , 已知点A到y轴的距离是4,那么点A的坐标为.
13. 如图,平分 , 于点C,且 , 已知点A到y轴的距离是4,那么点A的坐标为. 14. 如图,在中, , , 垂足分别为D,E, , 交于点H,已知 , , 则 .
14. 如图,在中, , , 垂足分别为D,E, , 交于点H,已知 , , 则 . 15. 如图,在中, , , D,E分别是边、上的点,将沿折叠,使点F落在的下方,当的边与平行时,的度数是 .
15. 如图,在中, , , D,E分别是边、上的点,将沿折叠,使点F落在的下方,当的边与平行时,的度数是 .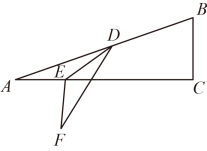 16. 如图,在等边中,于D,E是线段上一点,F是边上一点,且满足 , G是的中点,连接 , 则下列四个结论:①;②;③;④;⑤当时, , 其中正确的有.(填序号)
16. 如图,在等边中,于D,E是线段上一点,F是边上一点,且满足 , G是的中点,连接 , 则下列四个结论:①;②;③;④;⑤当时, , 其中正确的有.(填序号)
三、解答题
-
17. 如图,在中, , , , 求的度数.
 18. 如图, , , , 求证: .
18. 如图, , , , 求证: . 19. 如图,在边长为1个单位长度的小正方形组成的网格中,的顶点均在格点上,点A的坐标为 , 点B的坐标为 , 点C的坐标为.
19. 如图,在边长为1个单位长度的小正方形组成的网格中,的顶点均在格点上,点A的坐标为 , 点B的坐标为 , 点C的坐标为. (1)、画出关于y轴对称的;(2)、若点D在格点上,且与全等,请写出满足条件的点D的坐标.(点D不与点B重合)20. 如图,点C在线段上, , , 求证:是等边三角形.
(1)、画出关于y轴对称的;(2)、若点D在格点上,且与全等,请写出满足条件的点D的坐标.(点D不与点B重合)20. 如图,点C在线段上, , , 求证:是等边三角形.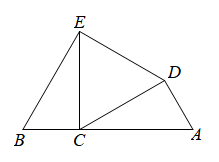 21. 已知:在中 , , .
21. 已知:在中 , , . (1)、试用尺规作图法,在上求作一点D,使;(要求保留作图痕迹,不写作法)(2)、在(1)的条件下,试确定线段、、的数量关系,并说明理由.
(1)、试用尺规作图法,在上求作一点D,使;(要求保留作图痕迹,不写作法)(2)、在(1)的条件下,试确定线段、、的数量关系,并说明理由.