河北省保定市第十七中教育集团八年级2022-2023学年八年级上学期数学期中反馈试题

试卷更新日期：2022-11-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数：3.141592， $- \sqrt{3}$ ， 0.16， $\sqrt{1 0^{- 2}}$ ， $- π$ ， 2.010010001，...(相邻两个1之间0的个数逐次加1)， $\frac{22}{7}$ ， $\sqrt[3]{5}$ ， $0.2 \dot{3}$ ， $\sqrt{8}$ 是无理数的有（）个.

A、2 B、3 C、4 D、5

查看试题解析
2. 下列各组数中，是勾股数的是（　　）

A、1，1， $\sqrt{2}$ B、1.5，2.5，2 C、4，5，6 D、9，12，15

查看试题解析
3. 下列计算中，正确的是（　　）．

A、 $\sqrt{4} = \pm 2$ B、 $- \sqrt{25} = 5$ C、 $\sqrt{{(- 7)}^{2}} = - 7$ D、 $\sqrt[3]{- 8} = - 2$

查看试题解析
4. 在平面直角坐标系的第四象限内有一点M，到x轴的距离为4，到y轴的距离为5，则点M的坐标为（）

A、 $(- 4 ， 5)$ B、 $(- 5 ， 4)$ C、 $(4 ， - 5)$ D、 $(5 ， - 4)$

查看试题解析
5. 一次函数 $y = - x + 2$ 与y轴的交点是（　　　）

A、（0，2） B、（0， $- 2$ ） C、（2，0） D、（ $- 2$ ， 0）

查看试题解析
6. 如图，小石同学在正方形网格中确定点A的坐标为（-1，1），点B的坐标为（2，0），则点C的坐标为（　　）

A、（1，-2） B、（-2，1） C、（-1，-2） D、（1，-1）

查看试题解析
7. 下列说法正确的是（）

A、-2是 ${(- 2)}^{2}$ 的算术平方根 B、3是-9的算术平方根 C、16的平方根是±4 D、27的立方根是±3

查看试题解析
8. 已知点A（m-1，m+4）在y轴上，则点A的坐标是（）

A、（0，3） B、（0，5） C、（5，0） D、（3，0）

查看试题解析
9. 第24届冬季奥林匹克运动会将于2022年由北京市和张家口市联合举行．以下能够准确表示张家口市地理位置的是（）

A、离北京市200千米 B、在河北省 C、在宁德市北方 D、东经114.8°，北纬40.8°

查看试题解析
10. 下列图象中，表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
11. 如果一次函数 $y = m x - m^{2} + m$ 的图象经过原点，则m的值为（）

A、0或1 B、1 C、0 D、不存在

查看试题解析
12. 已知点 $A (- 1 ， y_{1})$ 和点 $B (2 ， y_{2})$ 都在一次函数 $y = 2 x + b$ 的图象上，则 $y_{1}$ 与 $y_{2}$ 的大小是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、不确定

查看试题解析
13. 如图，一棵大树在一次强台风中于离地面10m处折断倒下，倒下部分的树梢到树的距离为24m，则这棵大树折断处到树顶的长度是（　　）

A、10m B、15m C、26m D、30m

查看试题解析
14. 在同一坐标系中，函数 $y = k x$ 与 $y = x - k$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
15. 我们可以用平方之后再开方的方式来化简一些有特点的无理数，如：对于 $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ ，设 $x = \sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ ，易知 $\sqrt{3 + \sqrt{5}} > \sqrt{3 - \sqrt{5}}$ ，故x＞0，由 $x^{2} = {(\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}})}^{2} = 3 + \sqrt{5} + 3 - \sqrt{5} - 2 \sqrt{(3 + \sqrt{5}) (3 - \sqrt{5})} = 2$ ，解得 $x = \sqrt{2}$ ，即 $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}} = \sqrt{2}$ ．根据以上方法，化简 $\sqrt{6 + 3 \sqrt{3}} - \sqrt{6 - 3 \sqrt{3}}$ 后的结果为（）

A、 $\sqrt{6}$ B、﹣12 C、 $- \sqrt{6}$ D、 $- 6 \sqrt{3}$

查看试题解析
16. 如图，在平面直角坐标系上有点 $A_{0}$ （1，0），点 $A_{0}$ 第一次跳动至点A（-1，1），第二次点 $A_{1}$ 跳动至点 $A_{2}$ （2，1），第三次点 $A_{2}$ 跳动至点 $A_{3}$ （-2，2），第四次点 $A_{3}$ 跳动至点 $A_{4}$ （3，2），……依此规律跳动下去，则点 $A_{2021}$ 与点 $A_{2022}$ 之间的距离是（）

A、2023 B、2022 C、2021 D、2020

查看试题解析

二、填空题

17. 点P（4，-3）关于x轴对称的点的坐标是，关于y轴对称的点的坐标是

查看试题解析
18. 已知一次函数 $y = a x + | a - 1 |$ 的图象经过点（0，3），且函数y的值随x的增大而减小，则a的值为．

查看试题解析
19. 已知a、b、c是 $△ A B C$ 的三边长，且满足关系 ${(a^{2} - c^{2} + b^{2})}^{2} + | a - b | = 0$ ，则 $△ A B C$ 的形状为．

查看试题解析
20. 图，直角坐标系 $x O y$ 中，一次函数 $y = - \frac{1}{2} x + 5$ 的图象 $l_{l}$ 分别与x，y轴交于A，B两点，正比例函数的图象 $l_{2}$ 与 $l_{1}$ 交于点 $C (m ， 4)$ ，则m= ，一次函数 $y = k x + 1$ 的图象为 $l_{3}$ ，且 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 不能围成三角形，则k的值为.

查看试题解析

三、解答题

21. 计算

(1)、 $3 {(x + 1)}^{2} = 48$

(2)、 ${(\frac{1}{3} x - 3)}^{3} = 125$

(3)、 $\sqrt{8} - \sqrt{32} + 2 \sqrt{\frac{1}{2}}$

(4)、 $\frac{\sqrt{27} - \sqrt{12}}{\sqrt{3}}$

(5)、 $(2 \sqrt{3} + 1) (2 \sqrt{3} - 1) - (\sqrt{3} - 1)^{2}$

(6)、 $\sqrt[3]{8} - \sqrt{4} - \sqrt{(- 3)^{2}} + | 1 - \sqrt{2} |$ ；

查看试题解析
22. 如图，在直角坐标系中， $△ A B C$ 的位置如图所示，请回答下列问题：

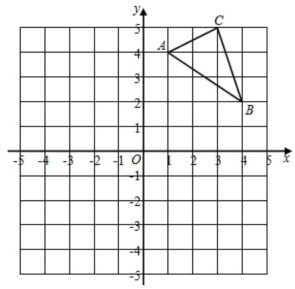(1)、请直接写出A、B、C三点的坐标、、.

(2)、画出 $△ A B C$ 关于x轴的对称图形 $△ A_{1} B_{1} C_{1}$ .

(3)、 $△ A B C$ 的面积为.

(4)、在x轴上找到一点P，使 $△ A B P$ 的周长最小，直接写出这个周长的最小值：.

查看试题解析
23. 如图，甲乙两船从港口A同时出发，甲船以10海里/时速度向北偏东 $48 °$ 航行，乙船向南偏东 $42 °$ 航行，5小时后，甲船到达C岛，乙船到达B岛，若C、B两岛相距130海里，问乙船的航速是多少？

查看试题解析
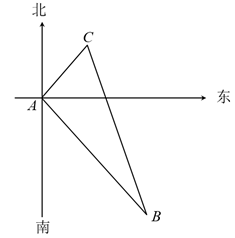24. 阅读下列一段文字，回答问题．
【材料阅读】平面内两点M（ $x_{1} ， y_{1}$ ），N（ $x_{2} ， y_{2}$ ），则由勾股定理可得，这两点间的距离MN= $\sqrt{（ x_{1} - x_{2} ）^{2} + {(y_{1} - y_{2})}^{2}}$ ．例如，M（3，1），N（1，－2），则MN= $\sqrt{（ 3 - 1 ）^{2} + {(1 + 2)}^{2}} = \sqrt{13} .$

(1)、【直接应用】
已知P（2，－3），Q（－1，3），求P、Q两点间的距离；

(2)、如图，在平面直角坐标系中，A（－1，－3），OB= $\sqrt{2}$ ， OB与 $x$ 轴正半轴的夹角是45°．
①求点B的坐标；
②试判断△ABO的形状．

查看试题解析
25. 小亮和爸爸登山，两人距离地面的高度y（米）与小亮登山时间x（分）之间的函数图象分别如图中折线 $O A - A C$ 和线段 $D E$ 所示，根据函数图象进行以下探究：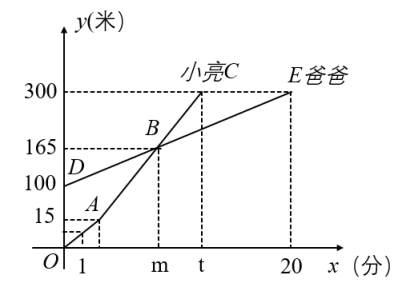

(1)、爸爸开始登山时距离地面米，登山的速度是每分钟米．

(2)、求爸爸登山时距地面的高度y（米）与登山时间x（分）之间的函数关系式．

(3)、小亮和爸爸什么时候相遇？求出相遇的时间．

(4)、若小亮提速后，他登山的速度是爸爸速度的3倍，问小亮登山多长时间时开始提速？

查看试题解析
26. 如图， $R t △ A B C$ ， $∠ A C B = 90 °$ ， $A C = B C$ ，已知点A和点C的坐标分别为 $(0 ， 2)$ 和 $(- 1 ， 0)$ ，过点A、B的直线关系式为 $y = k x + b$ .

(1)、点B的坐标为：．

(2)、求直线 $A B$ 的函数关系式．

(3)、在x轴上有一个点D，已知直线 $A D$ 把 $S_{△ A O N}$ 的面积分为 $1 ： 2$ 两部分，请直接写出点D的坐标．

(4)、在线段 $A N$ 上是否存在点P，使 $△ A C P$ 的面积为4?若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

(5)、直线 $y = - x + b$ 与 $△ A B C$ 有公共点，直接写出b的取值范围．

查看试题解析