北京市燕山地区2022-2023学年八年级上学期期中质量检测数学试题
试卷更新日期:2022-11-15 类型:期中考试
一、单选题
-
1. 第24届冬奥会于2022年2月20日在世界首个“双奥之城”—北京圆满落下帷幕.下面是从历届冬奥会的会徽中选取的部分图形,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段,能组成三角形的是( )A、1,2,3 B、2,3,4 C、2,3,6 D、4,6,103. 在中, , 于点D,若 , 则( )A、2 B、3 C、4 D、54. 中, , , 则( )A、2 B、3 C、4 D、55. 下列多边形中,内角和为720°的是( )A、
2. 下列长度的三条线段,能组成三角形的是( )A、1,2,3 B、2,3,4 C、2,3,6 D、4,6,103. 在中, , 于点D,若 , 则( )A、2 B、3 C、4 D、54. 中, , , 则( )A、2 B、3 C、4 D、55. 下列多边形中,内角和为720°的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图, , , 则的度数为( )
6. 如图, , , 则的度数为( ) A、 B、 C、 D、7. 如图所示在 中, 边上的高线画法正确的是( )A、
A、 B、 C、 D、7. 如图所示在 中, 边上的高线画法正确的是( )A、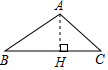 B、
B、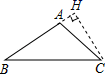 C、
C、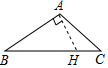 D、
D、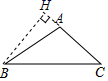 8. 点P在的角平分线上,点P到边的距离为10,点Q是边上任意一点,则的最小值为( )A、6 B、8 C、10 D、129. 如图,在中,垂直平分 , 交 于D,交于E,则的周长为( )
8. 点P在的角平分线上,点P到边的距离为10,点Q是边上任意一点,则的最小值为( )A、6 B、8 C、10 D、129. 如图,在中,垂直平分 , 交 于D,交于E,则的周长为( ) A、12 B、14 C、16 D、1810. 在平面直角坐标系中,横、纵坐标都是整数的点叫做格点.如图,点A的坐标为 , 点B的坐标为 , 点C为第一象限内的格点,若不共线的A,B,C三点构成轴对称图形,则满足条件的点C的个数为( )
A、12 B、14 C、16 D、1810. 在平面直角坐标系中,横、纵坐标都是整数的点叫做格点.如图,点A的坐标为 , 点B的坐标为 , 点C为第一象限内的格点,若不共线的A,B,C三点构成轴对称图形,则满足条件的点C的个数为( ) A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题
-
11. 平面直角坐标系中,点(3,-2)关于x轴对称的点的坐标是 .12. 如图,在△ABC中,点D在BC的延长线上,若∠A=60°,∠B=40°,则∠ACD的度数是 .
 13. 已知直角三角形中30°角所对的直角边为2cm,则斜边的长度为cm.14. 工人师傅做门时,常用木条固定长方形门框,使其不变形,这种做法的根据是 .15. 如图,用直尺和圆规作一个角等于已知角的过程中,依据全等三角形的性质可得 , 这里判断的依据是 .
13. 已知直角三角形中30°角所对的直角边为2cm,则斜边的长度为cm.14. 工人师傅做门时,常用木条固定长方形门框,使其不变形,这种做法的根据是 .15. 如图,用直尺和圆规作一个角等于已知角的过程中,依据全等三角形的性质可得 , 这里判断的依据是 . 16. 等腰三角形的顶角度数为 , 则它的底角度数为 .17. 已知等腰三角形两边长分别为3cm和5cm,则等腰三角形的周长为cm.18. 如图,在平面直角坐标系中,可以看作是经过若干次的图形变化(平移、轴对称)得到,请写出一种由得到的过程 .
16. 等腰三角形的顶角度数为 , 则它的底角度数为 .17. 已知等腰三角形两边长分别为3cm和5cm,则等腰三角形的周长为cm.18. 如图,在平面直角坐标系中,可以看作是经过若干次的图形变化(平移、轴对称)得到,请写出一种由得到的过程 .
三、解答题
-
19. 如图,已知 , , , 求证:ab.
 20. 如图,中,的平分线交于点D,过点D作 , 交于点E.若 , 求 .
20. 如图,中,的平分线交于点D,过点D作 , 交于点E.若 , 求 . 21. 如图,点A,F,C,D在同一直线上, , 请你再添加一个条件,使得 , 并证明.
21. 如图,点A,F,C,D在同一直线上, , 请你再添加一个条件,使得 , 并证明. 22. 如图,格点△ABC在网格中的位置如图所示.
22. 如图,格点△ABC在网格中的位置如图所示.
( 1 )画出△ABC关于直线MN的对称△A'B'C';
( 2 )若网格中每个小正方形的边长为1,则△A'B'C'的面积为 ;
( 3 )在直线MN上找一点P,使PA+PC最小(不写作法,保留作图痕迹).
23. 数学课上,王老师布置如下任务:如图,已知∠MAN<45°,点B是射线AM上的一个定点,在射线AN上求作点C,使∠ACB=2∠A.
下面是小路设计的尺规作图过程.
作法:①作线段AB的垂直平分线l,直线l交射线AN于点D;
②以点B为圆心,BD长为半径作弧,交射线AN于另一点C,则点C即为所求.

根据小路设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明:证明:连接BD,BC,
∵直线l为线段AB的垂直平分线,
∴DA= ▲ , ( )(填推理的依据)
∴∠A=∠ABD,
∴∠BDC=∠A+∠ABD=2∠A.
∵BC=BD,
∴∠ACB=∠ ▲ , ( )(填推理的依据)
∴∠ACB=2∠A.
24. 如图:△ABC和△ADE是等边三角形,证明:BD=CE. 25. 如图,在中, , 点A在直线l上,于M,于
25. 如图,在中, , 点A在直线l上,于M,于 (1)、依题意补全图形;(2)、用等式表示之间的数量关系,并证明.26. 定义:过三角形的顶点作一条射线与其对边相交,将三角形分成两个三角形,若得到的两个三角形中有等腰三角形,这条射线就叫做原三角形的“和谐分割线”.
(1)、依题意补全图形;(2)、用等式表示之间的数量关系,并证明.26. 定义:过三角形的顶点作一条射线与其对边相交,将三角形分成两个三角形,若得到的两个三角形中有等腰三角形,这条射线就叫做原三角形的“和谐分割线”. (1)、下列三角形中,不存在“和谐分割线”的是 (只填写序号).
(1)、下列三角形中,不存在“和谐分割线”的是 (只填写序号).①等边三角形;②顶角为150°的等腰三角形;③等腰直角三角形.
(2)、如图1,在△ABC中,∠A=60°,∠B=40°,直接写出△ABC被“和谐分割线”分得到的等腰三角形顶角的度数;(3)、如图2,△ABC中,∠A=30°,CD为AB边上的高,BD=4,E为AD的中点,过点E作直线l交AC于点F,作CM⊥l于M,DN⊥l于N.若射线CD为△ABC的“和谐分割线”.求CM+DN的最大值.