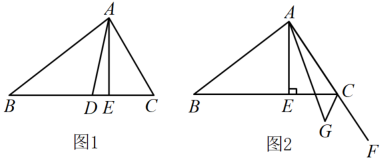山东省淄博市高青县2022-2023学年七年级上学期期中数学试题
试卷更新日期：2022-11-15 类型：期中考试
一、单选题
-
1. 北京2022年冬奥会会徽（冬梦），是第24届冬季奥林匹克运动会使用的标志，主要由会徽图形、文字标志、奥林匹克五环标志组成，组成会徽的四个图案中是轴对称图形的是（ ）
A、
B、
C、
D、
2. 如图，在中，边上的高是（ ）
A、线段 B、线段 C、线段 D、线段3. 如图，直线AO⊥OB，垂足为O，线段AO＝3，BO＝4，以点A为圆心，AB的长为半径画弧，交直线AO于点C．则OC的长为（ ）
A、5 B、4 C、3 D、24. 如图，把沿EF翻折，叠合后的图形如图，若 ， ， 则的度数是（ ）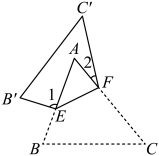
A、15° B、20° C、25° D、35°5. 如图，把一张长方形纸片ABCD沿EF折叠后，点A落在CD边上的点A'处，点B落在点B'处，若∠1＝115°，则图中∠2的度数为（ ）
A、40° B、45° C、50° D、60°6. 如图，在△ABC中，CD、BE分别是AB、AC边上的高，F是CD与BE的交点．若AD＝FD，∠ABE＝26°，则∠ACB的度数为（ ）
A、76° B、71° C、81° D、86°7. 如图，在方格纸中，以为一边作 ， 使之与全等，在方格的格点中找出符合条件的P点（不与点A，B，C重合），则点P有（ ）
A、1个 B、2个 C、3个 D、4个8. 如图，在△ABC中，的垂直平分线交 ， 于点 ， ． 若△ABC的周长为30， ， 则△ABD的周长为（ ）
A、10 B、15 C、20 D、259. 如图，在中，已知点D、E，F分别为、、的中点，且 ， 则阴影部分面积S=（ ） ．
A、1 B、2 C、3 D、410. 如图，已知锐角∠AOB，根据以下要求作图．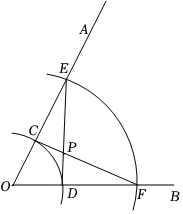
⑴在射线OA上取点C和点E，以点O为圆心，OC，OE的长为半径画弧，分别交射线OB于点D，F；
⑵连接CF，DE交于点P．
则下列结论错误的是（ ）
A、CE＝DF B、点P在∠AOB的平分线上 C、PE＝PF D、若∠AOB＝60°，则∠CPD＝120°二、填空题
-
11. 如图，若AB，CD相交于点E，若△ABC≌△ADE，∠BAC＝28°，则∠ACD的度数是 ．
12. 如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB于点D，如果AC＝6，AB＝8，则AE+DE等于 ．
13. 如图，已知BD是的中线， ， ， 和的周长的差是 ．
14. 如图，在中， ， 将按如图方式折叠，使点B与点A重合，折痕为 ， 则的长为 ．
15. 如图，“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒 ， 组成，两根棒在O点相连并可绕O转动，C点固定， ， 点D、E可在槽中滑动．若 ， 则的度数是 ．
三、解答题
-
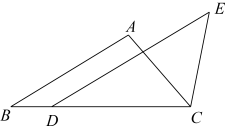
16. 如图，在△ABC中，点D在边BC上，CD=AB，DE∥AB，∠DCE=∠A.求证：DE=BC.
17. 如图，已知中， ， ， 是的角平分线，于E点．
(1)、求的度数；(2)、 ， ， ， 求 ．18. 用10块高度相同长方体小木块垒了两堵与地面垂直的木墙、 ， ， ， 两木墙之间刚好可以放进一个等腰直角三角板 ， 点C在上，点A和B分别与木墙的顶端重合，求两堵木墙之间的距离．
19. 如图，在△ABC中，CD⊥AB于点D，AC＝20，BC＝15，DB＝9．
(1)、求DC的长；(2)、求AB的长；(3)、求∠ACB的度数．20. 如图，在ABC中，D是边BC的中点，E是边AC的中点，连接AD，BE．
(1)、若CD＝8，CE＝6，AB＝20，求证：∠C＝90°；(2)、若∠C＝90°，AD＝13，AE＝6，求ABC的面积．
