山东省潍坊市青州市2022-2023学年七年级上学期期中数学试题
试卷更新日期:2022-11-15 类型:期中考试
一、单选题
-
1. 下列四个选项中,不是正方体展开图形的是( )A、
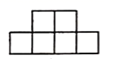 B、
B、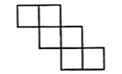 C、
C、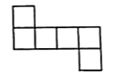 D、
D、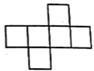 2. 将6+(+3)+(﹣7)-(﹣2)改写成省略括号的和的形式是( )A、﹣6﹣3+7﹣2 B、6﹣3﹣7+2 C、6﹣3+7﹣2 D、6+3-7+23. 某校有3000名学生在线观看了“天宫课堂”第二课,并参加了关于“你最喜爱的太空实验”的问卷调查,从中抽取500名学生的调查情况进行统计分析,以下说法错误的是( )A、3000名学生的问卷调查情况是总体 B、500名学生的问卷调查情况是样本 C、500名学生是样本容量 D、每一名学生的问卷调查情况是个体4. 如图,数轴上的两个点分别表示数a和-2,则a可以是( )
2. 将6+(+3)+(﹣7)-(﹣2)改写成省略括号的和的形式是( )A、﹣6﹣3+7﹣2 B、6﹣3﹣7+2 C、6﹣3+7﹣2 D、6+3-7+23. 某校有3000名学生在线观看了“天宫课堂”第二课,并参加了关于“你最喜爱的太空实验”的问卷调查,从中抽取500名学生的调查情况进行统计分析,以下说法错误的是( )A、3000名学生的问卷调查情况是总体 B、500名学生的问卷调查情况是样本 C、500名学生是样本容量 D、每一名学生的问卷调查情况是个体4. 如图,数轴上的两个点分别表示数a和-2,则a可以是( ) A、 B、 C、0 D、25. 如图所示,某同学的家在P处,他想尽快赶到附近C处搭顺风车,他选择第②条路线,用几何知识解释其道理正确的是( )
A、 B、 C、0 D、25. 如图所示,某同学的家在P处,他想尽快赶到附近C处搭顺风车,他选择第②条路线,用几何知识解释其道理正确的是( ) A、两点确定一条直线 B、两点之间,直线最短 C、两点之间,线段最短 D、经过一点有无数条直线6. 2022年4月18日,国家统计局发布初步核算,一季度国内生产总值270178亿元,同比增长4.8%,经济运行总体平稳.其中270178亿用科学记数法(精确到千亿位)表示为( )A、 B、 C、 D、7. 如果 , 则的值是( )A、 B、 C、 D、8. 乐乐在数学学习中遇到了神奇的“数值转换机”,按如图所示的程序运算,若输入一个有理数x,则可相应的输出一个结果y.若输入x的值为-1,则输出的结果y为( )
A、两点确定一条直线 B、两点之间,直线最短 C、两点之间,线段最短 D、经过一点有无数条直线6. 2022年4月18日,国家统计局发布初步核算,一季度国内生产总值270178亿元,同比增长4.8%,经济运行总体平稳.其中270178亿用科学记数法(精确到千亿位)表示为( )A、 B、 C、 D、7. 如果 , 则的值是( )A、 B、 C、 D、8. 乐乐在数学学习中遇到了神奇的“数值转换机”,按如图所示的程序运算,若输入一个有理数x,则可相应的输出一个结果y.若输入x的值为-1,则输出的结果y为( ) A、 B、7 C、10 D、12
A、 B、7 C、10 D、12二、多选题
-
9. (多选题)点A,B在数轴上的位如图所示,它们对应的有理数分别是a,b,则以下结论正确的是( )
 A、 B、 C、 D、10. 某工厂生产工艺品,以每天生产35个为基本量,实际每天生产量与前一天相比有增减(上周最后一天生产量恰好是基本量,超产记为正,减产记为负).如表是本周一至周五的生产情况:
A、 B、 C、 D、10. 某工厂生产工艺品,以每天生产35个为基本量,实际每天生产量与前一天相比有增减(上周最后一天生产量恰好是基本量,超产记为正,减产记为负).如表是本周一至周五的生产情况:星期
一
二
三
四
五
增减(单位:个)
根据记录的数据,该厂本周每天生产量超过基本量35个的是( )
A、星期二 B、星期三 C、星期四 D、星期五11. 如图,是超市2~6月份销售额每月比上月增长率的统计图,下列说法错误的有( ) A、4月份的销售额低于3月份 B、销售额每月比上月增长率低于9%的有2个月份 C、销售额最多的是5月份 D、销售额每月比上月的增长率有大有小,但销售额一直在持续增加12. 定义运算 , 下面关于这种运算的四个结论是“我爱数学”学习小组给出的,其中正确的是( )A、 B、若 , 则或 C、 D、
A、4月份的销售额低于3月份 B、销售额每月比上月增长率低于9%的有2个月份 C、销售额最多的是5月份 D、销售额每月比上月的增长率有大有小,但销售额一直在持续增加12. 定义运算 , 下面关于这种运算的四个结论是“我爱数学”学习小组给出的,其中正确的是( )A、 B、若 , 则或 C、 D、三、填空题
-
13. 如图,点在线段上,且 , 点是线段的中点.若 , 则的长为 .
 14. 绝对值小于2.5的非负整数有 .15. 1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:正整数5经过下面5步运算可得到1,即: . 则正整数6经过步运算可得到1.16. 若 , 则a= .
14. 绝对值小于2.5的非负整数有 .15. 1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:正整数5经过下面5步运算可得到1,即: . 则正整数6经过步运算可得到1.16. 若 , 则a= .四、解答题
-
17. 把下列各数填在合适的括号内:
1, , , 0, , , , .
(1)、正整数:{ …};(2)、整数:{ …};(3)、正分数:{ …};(4)、非负数:{ …}.18. 计算:(1)、(2)、(3)、19. 某中学开设了书法、绘画、乐团、合唱等艺术类社团,全校每名学生选择了其中一项活动,为了解学生的报名情况,张老师抽选了一部分学生进行调查,并绘制了两个不完整的统计图,请你依据统计图中的信息,回答下列问题: (1)、本次抽样调查共抽取了名学生;通过计算补全条形统计图;(2)、求图2中表示合唱的扇形圆心角的度数;(3)、若全校共有1600名学生,请你估计全校选择参加乐团的学生有多少名?20.(1)、若 , n的相反数是3,求m,n的值;(2)、若 , 求 .21. 小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题:
(1)、本次抽样调查共抽取了名学生;通过计算补全条形统计图;(2)、求图2中表示合唱的扇形圆心角的度数;(3)、若全校共有1600名学生,请你估计全校选择参加乐团的学生有多少名?20.(1)、若 , n的相反数是3,求m,n的值;(2)、若 , 求 .21. 小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题: (1)、从中取出2张卡片,如何抽取能使这2张卡片上的数字乘积最大,并说明理由;(2)、从中取出2张卡片,如何抽取能使这2张卡片上的数字相除的商最小,并说明理由.22. 如图①,在数轴上有一条线段AB,点A,B表示的数分别是-2和-11.
(1)、从中取出2张卡片,如何抽取能使这2张卡片上的数字乘积最大,并说明理由;(2)、从中取出2张卡片,如何抽取能使这2张卡片上的数字相除的商最小,并说明理由.22. 如图①,在数轴上有一条线段AB,点A,B表示的数分别是-2和-11. (1)、若M是线段AB的中点,则点M在数轴上对应的数为 .(2)、若C为线段AB上一点,如图②,以点C为折点,将此数轴向右对折;如图③,点B落在点A的右边点B′处,若AB′=B′C,求点C在数轴上对应的数是多少?23. 观察下列两个等式: , 给出定义如下:我们称使等式成立的一对有理数a,b为“共生有理数对”,记为 .(1)、通过计算判断有理数对“-2,1”、“4,”是不是“共生有理数对”;(2)、若是“共生有理数对”,求a的值.(3)、若是“共生有理数对”,则“n,m”是不是 “共生有理数对”.
(1)、若M是线段AB的中点,则点M在数轴上对应的数为 .(2)、若C为线段AB上一点,如图②,以点C为折点,将此数轴向右对折;如图③,点B落在点A的右边点B′处,若AB′=B′C,求点C在数轴上对应的数是多少?23. 观察下列两个等式: , 给出定义如下:我们称使等式成立的一对有理数a,b为“共生有理数对”,记为 .(1)、通过计算判断有理数对“-2,1”、“4,”是不是“共生有理数对”;(2)、若是“共生有理数对”,求a的值.(3)、若是“共生有理数对”,则“n,m”是不是 “共生有理数对”.