山东省青岛市莱西市2022-2023学年七年级上学期期中数学试题
试卷更新日期:2022-11-15 类型:期中考试
一、单选题
-
1. 下列关于数字变换的图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三根木棒能组成三角形的是( )A、3,4,8 B、4,4,8 C、5,6,10 D、6,7,143. 该图形从哪个方向看是轴对称图形( )
2. 下列长度的三根木棒能组成三角形的是( )A、3,4,8 B、4,4,8 C、5,6,10 D、6,7,143. 该图形从哪个方向看是轴对称图形( ) A、从正面看 B、从上面看 C、从左面看 D、都不是4. 画△ABC的边AB上的高,下列画法中,正确的是( )A、
A、从正面看 B、从上面看 C、从左面看 D、都不是4. 画△ABC的边AB上的高,下列画法中,正确的是( )A、 B、
B、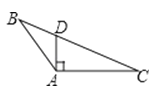 C、
C、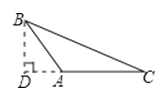 D、
D、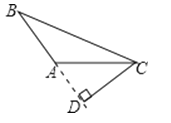 5. 下列说法正确的是( )A、角是轴对称图形,角平分线是它的对称轴 B、等腰三角形是轴对称图形;底边中线是它的对称轴 C、线段是轴对称图形,中垂线是它的一条对称轴 D、所有的直角三角形都不是轴对称图形6. 下列哪组数可以作为直角三角形的三边长( )A、9,40,41 B、 , , C、 , , D、2,3,57. 如图,在中,平分 , 于点E,再添加一个条件仍然不能证明的是( )
5. 下列说法正确的是( )A、角是轴对称图形,角平分线是它的对称轴 B、等腰三角形是轴对称图形;底边中线是它的对称轴 C、线段是轴对称图形,中垂线是它的一条对称轴 D、所有的直角三角形都不是轴对称图形6. 下列哪组数可以作为直角三角形的三边长( )A、9,40,41 B、 , , C、 , , D、2,3,57. 如图,在中,平分 , 于点E,再添加一个条件仍然不能证明的是( ) A、 B、 C、 D、8. 如图, , 且 , , , 则线段AE的长为( )
A、 B、 C、 D、8. 如图, , 且 , , , 则线段AE的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 下列说法正确的是(填序号)
①三角形的三条角平分线相交于一点 ②三角形的三条高相交于一点
③全等三角形的面积相等 ④面积相等的三角形全等
10. 请你发现下图的规律,在空格上画出第4个图案.
 11. 一副直角三角板如图放置,点C在的延长线上, , , 则的度数为 .
11. 一副直角三角板如图放置,点C在的延长线上, , , 则的度数为 . 12. 海面上有两个疑似漂浮目标.A舰艇以12海里/时的速度离开港口O,向北偏西方向航行;同时,B舰艇在同地以16海里/时的速度向北偏东一定角度的航向行驶,如图所示,离开港口5小时后两船相距100海里,则B舰艇的航行方向是 .
12. 海面上有两个疑似漂浮目标.A舰艇以12海里/时的速度离开港口O,向北偏西方向航行;同时,B舰艇在同地以16海里/时的速度向北偏东一定角度的航向行驶,如图所示,离开港口5小时后两船相距100海里,则B舰艇的航行方向是 . 13. 如图,与关于直线对称,若 , , 则的度数为 .
13. 如图,与关于直线对称,若 , , 则的度数为 . 14. 如图,一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,则最少要爬行cm.
14. 如图,一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,则最少要爬行cm. 15. 如图,在△ABC中,AB=AC,∠C=30°,AD⊥AB,交BC于点D且AD=1,则BC=
15. 如图,在△ABC中,AB=AC,∠C=30°,AD⊥AB,交BC于点D且AD=1,则BC= 16. 如图,小巷左右两侧是竖直的墙,一根竹竿斜靠在右墙时,竹竿底端到右墙角的距离为15米,顶端距离地面20米;如果保持竹竿底端位置不动,将竹竿斜靠在左墙时,其顶端距离地面为24米,则小巷的宽度为米.
16. 如图,小巷左右两侧是竖直的墙,一根竹竿斜靠在右墙时,竹竿底端到右墙角的距离为15米,顶端距离地面20米;如果保持竹竿底端位置不动,将竹竿斜靠在左墙时,其顶端距离地面为24米,则小巷的宽度为米.
三、解答题
-
17. 如图,两个班的学生分别在两处参加植树劳动,现要在道路的交叉区域内设一个饮水供应点P,使P到两条道路的距离相等,且使有一同学说:“只要作一个角平分线、一条线段的垂直平分线,这个饮水供应点的位置就确定了”,你认为这位同学说得对吗?请用尺规作图找到饮水供应点P的位置,并说明理由.
 18. 在3×3的正方形格点图中,和是关于某条直线成轴对称的两个格点三角形(三角形顶点都是小正方形顶点),现给出了 , 在下面的图中画出4个符合条件的 .
18. 在3×3的正方形格点图中,和是关于某条直线成轴对称的两个格点三角形(三角形顶点都是小正方形顶点),现给出了 , 在下面的图中画出4个符合条件的 . 19. 已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
19. 已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.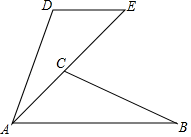 20. 如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水,然后沿另一方向走80m到达菜地C处浇水,最后沿第三方向走100m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
20. 如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水,然后沿另一方向走80m到达菜地C处浇水,最后沿第三方向走100m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由. 21. 如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
21. 如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E. (1)、求证:AB=AE;(2)、若∠A=100°,求∠EBC的度数.22. 王强同学用10块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 ,点C在 上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
(1)、求证:AB=AE;(2)、若∠A=100°,求∠EBC的度数.22. 王强同学用10块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 ,点C在 上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离. 23. 如图,已知是等边三角形,D为AC上一点, , .
23. 如图,已知是等边三角形,D为AC上一点, , . (1)、与全等吗?为什么?(2)、是等边三角形吗?请说明理由.24. 如图,一棵高的大树在一次暴风雨中被刮断,树顶C落在离树根B点处.研究人员要查看断痕A处的情况,在离树根的D处竖起一架梯子 , 请问这架梯子的长是多少?
(1)、与全等吗?为什么?(2)、是等边三角形吗?请说明理由.24. 如图,一棵高的大树在一次暴风雨中被刮断,树顶C落在离树根B点处.研究人员要查看断痕A处的情况,在离树根的D处竖起一架梯子 , 请问这架梯子的长是多少?


