山东省济南市长清区2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-11-15 类型：期中考试

进入出卷网下载

一、单选题

1. $- 2022$ 的相反数是（　　）

A、 $- \frac{1}{2022}$ B、 $\frac{1}{2022}$ C、 $- 2022$ D、 $2022$

查看试题解析
2. 第24届冬季奥林匹克运动会即2022年北京冬季奥运会计划于2022年2月4日至2022年2月20日召开，届时总建筑面积约为333000平方米的北京冬奥村将迎来北京赛区运动员及随行官员在此居住．将数字333000用科学记数法表示应为（）

A、 $0.333 \times 1 0^{7}$ B、 $3.33 \times 1 0^{5}$ C、 $3.33 \times 1 0^{4}$ D、 $33.3 \times 1 0^{4}$

查看试题解析
3. 下列选项中，不是正方体表面展开图的是（）

A、 B、 C、 D、

查看试题解析
4. 在下列数 $- \frac{5}{6}$ ， $+ 1$ ， $6.7$ ， $- 15$ ， $0$ ， $\frac{22}{7}$ ， $- (- 1)$ ， $25 %$ 中，属于整数的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 某正方体的平面展开图如图所示，则原正方体中与“春”字所在的面相对的面上的字是（）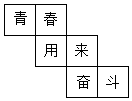

A、青 B、来 C、斗 D、奋

查看试题解析
6. 若 $- 5 x^{a} z^{b}$ 与 $7 x^{3} z^{2}$ 是同类项，则 $a b$ 的值是（）

A、9 B、5 C、6 D、 $- 9$

查看试题解析

7. 某市11月4日至7日天气预报的最高气温与最低气温如表：

日期	11月4日	11月5日	11月6日	11月7日
最高气温（℃）	19	12	20	19
最低气温（℃）	4	﹣3	4	5

其中温差最大的一天是（）

A、11月4日 B、11月5日 C、11月6日 D、11月7日

查看试题解析

8. 已知a，b两数在数轴上对应的点如图所示，在下列结论中，①b＞a；②a+b＞0；③a﹣b＞0；④ab＜0；⑤ $\frac{b}{a}$ ＞0；正确的是（）

A、①②⑤ B、③④ C、③⑤ D、②④

查看试题解析
9. 某商品进价为400元，标价x元，在商场开展的促销活动中，该商品按8折销售，那么该商品仍可以获利（）

A、 $(8 x - 400)$ 元 B、 $(400 \times 8 - x)$ 元 C、 $(0.8 \times 400 - x)$ 元 D、 $(0.8 x - 400)$ 元

查看试题解析
10. 形如 $a_{1} a_{2} \dots {a_{n}}_{－ 1} a_{n} {a_{n}}_{－ 1} a_{2} a_{1}$ 的自然数(其中 n为正整数， $a_{1} \leq a_{2} \leq \dots \leq {a_{n}}_{－ 1} \leq a_{n}$ ， $a_{1} > 0 ， a_{1} ， a_{2} ， \dots$ ， $a_{n}$ 为 $0 ， 1 ， \dots ， 9$ 中的数字)称为“单峰回文数”，不超过5位的“单峰回文数”的个数是（）

A、273 B、219 C、429 D、129

查看试题解析

二、填空题

11. 《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数，若其意义相反，则分别叫作正数与负数，如果向东走5米记为 $+ 5$ 米，那么向西走3米记为米；

查看试题解析
12. 单项式 $- \frac{3}{4} x^{2} y$ 的系数是；

查看试题解析
13. 比较两数大小：﹣ $\frac{1}{5}$ ﹣ $\frac{1}{3}$ （用“＜”或“＝”或“＞”填空）.

查看试题解析
14. 若 $| m - 2 | + {(n + 3)}^{2} = 0$ ，则 $m - n =$ ．

查看试题解析
15. 已知多项式 $3 x^{p} - (q + 2) x + 1$ 是关于x的三次二项式，则 $q^{p} =$ ；

查看试题解析
16. 我们把对非负数x “四舍五入”到个位的值记为 $《 x 》$ ，即当n为非负整数时，若 $n - \frac{1}{2} \leq x < n + \frac{1}{2}$ ，则 $《 x 》 = n$ ，例如 $《 0.67 》 = 1 ，《 2.49 》 = 2 ，$ 下列结论中：① $《 2 x 》 = 2 《 x 》$ ；②当m为非负整数时， $《 m + 2 x 》 = m + 《 2 x 》$ ；③满足 $《 x 》 = \frac{3}{2} x$ 的非负整数x只有两个．其中结论正确的是(填序号)

查看试题解析

三、解答题

17. 计算：

(1)、 $15 - (- 2) + (- 7)$ ；

(2)、 $(- 36) \div 3 \times (- \frac{1}{3})$ ．

查看试题解析
18. 画出下面几何体从三个方向看到的三种形状图．

查看试题解析
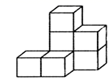19. 在数轴上表示下列各数：-3，2， $2.5$ ， $- \frac{1}{2}$ ，并将这些数用“<”连接．

查看试题解析
20. 计算：

(1)、 $(- \frac{1}{2} - \frac{1}{3} + \frac{3}{4}) \times (- 60)$ ；

(2)、 $- 3^{2} \times \frac{1}{2} + (- 4)^{2} \div (- 4)$ ．

查看试题解析
21. 若a，b互为相反数，c，d互为倒数，m的绝对值为2，求 $(a + b)^{2020} + (- c d)^{2023} - m^{2}$ 的值．

查看试题解析
22. 对于有理数a、b规定一种新运算： $a @ b = 2 a b - b$ ．

(1)、求 $3 @ 4$ 的值；

(2)、计算： $5 @ [(- 2) @ 4]$ 的值．

查看试题解析
23. 为了有效遏制酒后驾车行为，区交警大队的一辆警车在城区大学路上巡逻，如果规定向东为正，向西为负，在某段时间内，这辆警车从出发点开始所走的路程为： $+ 8$ ， $- 5$ ， $+ 2$ ， $- 10$ ， $+ 3$ ， $- 4$ ， $+ 6$ ， $- 3$ (单位：千米)

(1)、巡逻结束时，这辆警车在出发点的哪个方向?距离出发点多远?

(2)、如果每千米耗油0.2升，在这段时间内巡逻共耗油多少升?

查看试题解析
24. 小亮房间窗户的窗帘如图(1)所示，它是由两个四分之一圆组成(半径相同)．

(1)、如图(1)，请用代数式表示装饰物的面积：；用代数式表示窗户能射进阳光的面积：；(结果保留 $π$ )．

(2)、小亮又设计了如图(2)的窗帘(由一个半圆和两个四分之一圆组成，半径相同)，请你用代数式表示窗户能射进阳光的面积：；

(3)、当 $a = 5$ 米， $b = 4$ 米时，两图中窗户能射进阳光的面积相差多少? ( $π$ 取3)

查看试题解析
25. 已知 $a 、 b$ 为常数，且满足 $| a - 12 | + {(b + 20)}^{2} = 0$ ，其中 $a 、 b$ 分别为点A、点B在数轴上表示的数，如图所示，动点 $E 、 F$ 分别从 $A 、 B$ 同时开始运动，点E以每秒 $6$ 个单位向左运动，点F以每秒 $2$ 个单位向右运动，设运动时间为 $t$ 秒．

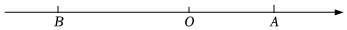(1)、求a、b的值：

(2)、请用含t的代数式表示点E在数轴上对应的数为：；点F在数轴上对应的数为：；

(3)、当E、F相遇后，点E继续保持向左运动，点F在原地停留 $4$ 秒后向左运动且速度变为原来的 $5$ 倍，在整个运动过程中，当E、F之间的距离为 $2$ 个单位时，请直接写出运动时间t的值．

查看试题解析
26. 阅读材料，并根据材料解答下列问题：
材料一： $\frac{1}{1 \times 2} = 1 - \frac{1}{2} ； \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3} ； \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4} ； \frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5}$ ；
材料二： $1 = \frac{1 \times 2}{2} ； 1 + 2 = \frac{2 \times 3}{2} ； 1 + 2 + 3 = \frac{3 \times 4}{2} ； 1 + 2 + 3 + 4 = \frac{4 \times 5}{2}$ ；

(1)、 $\frac{1}{10 \times 11} =$ ； $1 + 2 + 3 + ⋯ + 10 =$ (请结合材料回答)；

(2)、结合材料一，化简： $\frac{1}{1 \times 2}$ ＋ $\frac{1}{2 \times 3}$ ＋ $\frac{1}{3 \times 4}$ ＋…＋ $\frac{1}{10 \times 11}$ ；

(3)、结合材料二，化简：1＋ $\frac{1}{1 + 2}$ ＋ $\frac{1}{1 + 2 + 3}$ ＋…＋ $\frac{1}{1 + 2 + 3 + ⋯ + 100}$ ．

查看试题解析