辽宁省丹东市东港市2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-11-15 类型：期中考试

进入出卷网下载

一、单选题

1. 用一个平面去截下列几何体，截得的平面图形不可能是三角形的有（　　）

A、0个 B、1个 C、2个 D、3个

查看试题解析
2. 下列哪个图形不可能是正方体的表面展开图（　　）

A、 B、 C、 D、

查看试题解析
3. 数轴上A点表示的数为3，点B与点A位于原点两侧且到原点的距离相等，点C与点B的距离为5，则点C表示的数为（　　）

A、2 B、 $- 5$ C、2或 $- 5$ D、2或 $- 8$

查看试题解析
4. 若要使得图中平面展开图折叠成正方体后，相对面上的两个数之和相等，则 $a + b + c$ 的值为（　　）

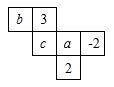A、12 B、7 C、5 D、－5

查看试题解析
5. 某商品原价为a元，经营者提价 $10 %$ 后，因市场物价调整，又降价 $10 %$ ，降价后这种商品的价格是（　　）

A、a元 B、 $0.88 a$ 元 C、 $0.96 a$ 元 D、 $0.99 a$ 元

查看试题解析
6. 若 $x^{2} - 3 x = 12$ 则代数式 $- 3 x^{2} + 9 x + 7$ 的值为（　　）

A、31 B、30 C、 $- 29$ D、 $- 31$

查看试题解析
7. 已知a与b的和为2，b与c互为相反数，若 $| c | = 1$ ，则a的值为（　　）

A、1或3 B、2或-4 C、3 D、3或-3

查看试题解析
8. 有理数a，b，c在数轴上的位置如图所示，则下列各式：
① $b c < 0$ ；② $a - c > 0$ ；③ $a + b + c < 0$ ；④ $| b + c | = c - b$ ．正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 有一个岛屿面积约为 $4380000 m^{2}$ ，这个数据用科学记数法表示为．

查看试题解析
10. 一个棱柱有15条棱，则这个棱柱有个顶点．

查看试题解析
11. 如果代数式 $- 7 a^{9} b^{2 m - 1}$ 与 $a^{4 n} b$ 的差是单项式，那么m-n= ．

查看试题解析
12. 一张厚度是0.1mm的纸，对折10次后，厚度为mm．

查看试题解析
13. 若 ${(a - 3)}^{2 n} + | b + 2 | = 0$ ，则 $b^{a}$ 的值为．

查看试题解析
14. 有一道题目是一个多项式减去 $x^{2} + 14 x - 5$ ，小明误当成了加法运算，结果得到了 $2 x^{2} - x + 3$ ，正确的结果应该是．

查看试题解析
15. 已知一个三位数A的百位数字是x，十位数字是y，个位数字是z，一个两位数B的十位数字是y，个位数字是x，则 $A - B$ 的值是．

查看试题解析
16. 用小立方体搭一个几何体，分别从它的正面、上面看到的形状如图所示．这样的几何体最少需个小立方体；最多需要个小立方体．

查看试题解析

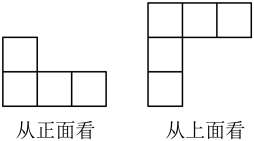
三、解答题

17.

(1)、 $- \frac{1}{2} + (- \frac{3}{2}) \div (- \frac{1}{3})$

(2)、 $- {(- 1)}^{2022} - {(- 1 \frac{1}{2})}^{3} \times \frac{2}{9} - 4 \div | - \frac{2}{3} |$

查看试题解析
18. 先化简，再求值： $4 x^{2} y - [6 x y - 3 (4 x y - 2) - x^{2} y] + 6$ ，其中 $x = - \frac{1}{2}$ ， $y = 2$ ．

查看试题解析
19. 小红为自己新家的房间窗户设计窗帘．

(1)、小红设计了如图（1）所示的窗帘，它是由两个四分之一圆组成（半径相同），请计算窗户能射进阳光的面积是多少？

(2)、小红又设计了如图（2）的窗帘（由一个半圆和两个四分之一圆组成，半径相同），请你帮她算一算图（2）窗户能射进阳光的面积是多少？哪个图窗户能射进阳光的面积更大？请求出大多少？

查看试题解析
20. 由7个相同的小立方块搭成的几何体如图所示，请画出从正面、左面、上面看到的几何体的形状图．

查看试题解析
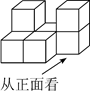21. 某电影院上映一部电影， $9$ 月 $30$ 日的票房为 $2.3$ 万元，接下来国庆假期 $7$ 天的票房变化情况如下表（正数表示比前一天增加的票房，负数表示比前一天减少的票房）
日期
$10.1$
$10.2$
$10.3$
$10.4$
$10.5$
$10.6$
$10.7$
票房（万元）
$+ 3.1$
$+ 1.2$
$- 0.8$
$+ 1.5$
$- 1$
$- 0.6$
$- 4$

(1)、国庆假期 $7$ 天中， $10$ 月 $3$ 日的票房收入是万元；

(2)、国庆假期 $7$ 天中，票房收入最多的一天是 $10$ 月日；

(3)、小明要求这7天票房的总收入，列式为： $2.3 \times 7 + (3.1 + 1.2 - 0.8 + 1.5 - 1 - 0.6 - 4)$ ，你认为他的列法是否正确，若正确请按他的方法求出结果；若错误，请按你认为正确的方法求出结果．

查看试题解析
22. 如图，在数轴上，点A，B，C的位置如图所示，点C与点A距离7个单位长度，点B与点A距离3个单位长度，点C表示的数是3．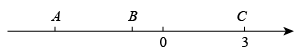

(1)、分别求出点A，点B表示的数；

(2)、点B与点C的距离是个单位长度；

(3)、若 $A D = 2 B C$ ，点P是 $D C$ 的中点，直接写出点P表示的数．

查看试题解析
23. 如图是由小正方体搭成的一个几何体从上面着到的形状图，小正方形中的数字表示在该位置的小正方体的个数，请你画出它从正面和从左面看到的形状图．

查看试题解析
24. 将边长相等的黑、白两色小正方形按如图所示的方式拼接起来，第1个图由5个白色小正方形和1个黑色小正方形拼接起来；第2个图由8个白色小正方形和2个黑色小正方形拼接起来；第3个图由11个白色小正方形和3个黑色小正方形拼接起来，依此规律拼接．

(1)、第4个图白色小正方形的个数为个；第8个图白色小正方形的个数为个；

(2)、第n个图白色小正方形的个数为个；

(3)、白色小正方形的个数为6068个，是第个图形；

(4)、是否存在某个图形，其白色小正方形的个数为2031个，若存在，求出是第几个图形；若不存在，请说明理由．

查看试题解析
25. 某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元，“国庆节”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一套西装送一条领带；
方案二：西装和领带都按定价的90%付款．
现某客户要到该商场购买西装20套，领带x条 $(x > 20)$ ．

(1)、若该客户按方案一购买，需付款元（用含x的代数式表示）；若该客户按方案二购买，需付款元（用含x的代数式表示）；

(2)、若 $x = 50$ ，通过计算说明此时方案一和方案二哪种购买方式较为合算；

(3)、当 $x = 50$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法，并计算需付款多少元．

查看试题解析

日期	$10.1$	$10.2$	$10.3$	$10.4$	$10.5$	$10.6$	$10.7$
票房（万元）	$+ 3.1$	$+ 1.2$	$- 0.8$	$+ 1.5$	$- 1$	$- 0.6$	$- 4$