2022年秋季湘教版数学九年级上册期末复习检测B
试卷更新日期:2022-11-15 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是s甲2=0.12,s乙2=0.59,s丙2=0.33,s丁2=0.46,在本次射击测试中,这四个人成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁2. 计算的结果,正确的是( )A、 B、 C、 D、3. 用配方法解一元二次方程时,将它化为的形式,则a+b的值为( )A、 B、 C、2 D、4. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )
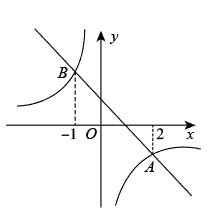 A、或 B、或 C、或 D、5. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )
A、或 B、或 C、或 D、5. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )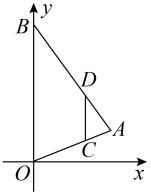 A、4 B、5 C、6 D、76. 已知关于x的一元二次方程(m﹣1)x2+2x﹣3=0有实数根,则m的取值范围是( )A、m≥ B、m< C、m>且m≠1 D、m≥且m≠17. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )
A、4 B、5 C、6 D、76. 已知关于x的一元二次方程(m﹣1)x2+2x﹣3=0有实数根,则m的取值范围是( )A、m≥ B、m< C、m>且m≠1 D、m≥且m≠17. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )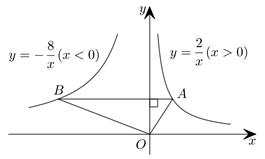 A、3 B、5 C、6 D、108. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )
A、3 B、5 C、6 D、108. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )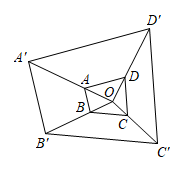 A、4 B、6 C、16 D、189. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A、4 B、6 C、16 D、189. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )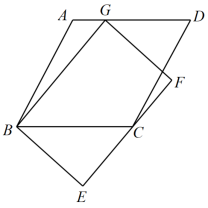 A、 B、 C、 D、310. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )
A、 B、 C、 D、310. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )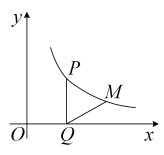 A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题(每题3分,共18分)
-
11. 如图,反比例函数的图象经过矩形对角线的交点E和点A,点B、C在x轴上,的面积为6,则 .
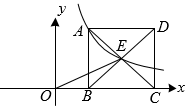 12. 设与为一元二次方程的两根,则的值为 .13. 如图,在 正方形网格中, 的顶点 、 、 都在网格线上,且都是小正方形边的中点,则 .
12. 设与为一元二次方程的两根,则的值为 .13. 如图,在 正方形网格中, 的顶点 、 、 都在网格线上,且都是小正方形边的中点,则 .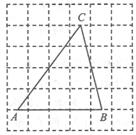 14. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB=cm.
14. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB=cm.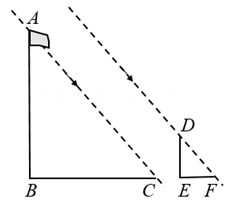 15. 如图,已知直角三角形中, , 将绕点点旋转至的位置,且在的中点,在反比例函数上,则的值为 .
15. 如图,已知直角三角形中, , 将绕点点旋转至的位置,且在的中点,在反比例函数上,则的值为 .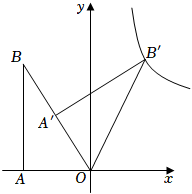 16. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .
16. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .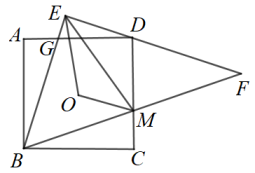
三、解答题(共9题,共72分)
-
17. 计算:18. 计算:2sin60°﹣|﹣2|+(π﹣)0﹣+(﹣)﹣2.19. 目前,全球淡水资源分布不均、总量不足是人类面临的共同问题,某市在实施居民用水定额管理前,通过简单随机抽样对居民生活用水情况进行了调查,获得了若干个家庭去年的月均用水量数据(单位:t),整理出了频数分布表,频数分布直方图和扇形统计图,部分信息如下:
月均用水量(t)
2≤x<3.5
3.5≤x<5
5≤x<6.5
6.5≤x<8
8≤x<9.5
频数
7
6
对应的扇形区域
A
B
C
D
E
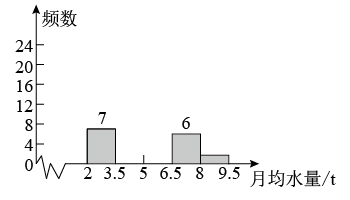

根据以上信息,解答下列问题:
(1)、补全频数分布直方图,并求出扇形图中扇形E对应的圆心角的度数;(2)、为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使该市60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?并说明理由.20. 交通安全心系千万家.高速公路管理局在某隧道内安装了测速仪,如图所示的是该段隧道的截面示意图.测速仪和测速仪到路面之间的距离 , 测速仪和之间的距离 , 一辆小汽车在水平的公路上由西向东匀速行驶,在测速仪处测得小汽车在隧道入口点的俯角为25°,在测速仪处测得小汽车在点的俯角为60°,小汽车在隧道中从点行驶到点所用的时间为38s(图中所有点都在同一平面内).
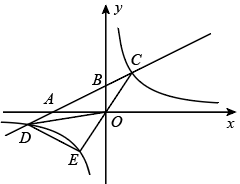
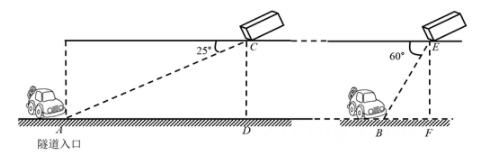 (1)、求 , 两点之间的距离(结果精确到1m);(2)、若该隧道限速22m/s,判断小汽车从点行驶到点是否超速?通过计算说明理由.(参考数据: , , , , , )21. 如图,一次函数与反比例函数的图象交于点 , 与轴交于点 .
(1)、求 , 两点之间的距离(结果精确到1m);(2)、若该隧道限速22m/s,判断小汽车从点行驶到点是否超速?通过计算说明理由.(参考数据: , , , , , )21. 如图,一次函数与反比例函数的图象交于点 , 与轴交于点 .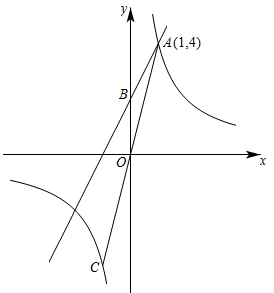 (1)、 , ;(2)、连接并延长 , 与反比例函数的图象交于点 , 点在轴上,若以、、为顶点的三角形与相似,求点的坐标.22. 建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.(1)、求该市改造老旧小区投入资金的年平均增长率;(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?23. 如图,在矩形ABCD中,AB=6,BC=4,点M、N分别在AB、AD上,且MN⊥MC,点E为CD的中点,连接BE交MC于点F.
(1)、 , ;(2)、连接并延长 , 与反比例函数的图象交于点 , 点在轴上,若以、、为顶点的三角形与相似,求点的坐标.22. 建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.(1)、求该市改造老旧小区投入资金的年平均增长率;(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?23. 如图,在矩形ABCD中,AB=6,BC=4,点M、N分别在AB、AD上,且MN⊥MC,点E为CD的中点,连接BE交MC于点F. (1)、当F为BE的中点时,求证:AM=CE;(2)、若=2,求的值;(3)、若MN∥BE,求的值.
(1)、当F为BE的中点时,求证:AM=CE;(2)、若=2,求的值;(3)、若MN∥BE,求的值.