山东省烟台招远市(五四制)2022-2023学年六年级上学期期中考试数学试题
试卷更新日期:2022-11-14 类型:期中考试
一、选择题(本大题共10个小题,每小题3分,满分30分)
-
1. 三棱柱的顶点个数是( )A、6 B、5 C、4 D、32. 如图是一些同学在作业中所画的数轴,其中,画图正确的是( )A、
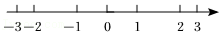 B、
B、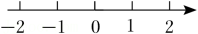 C、
C、 D、
D、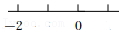 3. 在0,-(-1),(-3)2 , -32 , -|-3|,中,正数的个数为( )A、1个 B、2个 C、3个 D、4个4. 2022年高考期间,招远市某中学附近悬挂“招远学子加油”的祝福语,如图是一个立方体的展开图,那么在原立方体上,“招”字对面的字是( )
3. 在0,-(-1),(-3)2 , -32 , -|-3|,中,正数的个数为( )A、1个 B、2个 C、3个 D、4个4. 2022年高考期间,招远市某中学附近悬挂“招远学子加油”的祝福语,如图是一个立方体的展开图,那么在原立方体上,“招”字对面的字是( )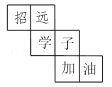 A、加 B、油 C、子 D、学5. 如果家用电冰箱冷藏室的温度是4℃,冷冻室的温度比冷藏室的温度低22℃,那么冷冻室的温度是( )A、18℃ B、-26℃ C、-22℃ D、-18℃6. 用四舍五入法对0.06045取近似值,错误的是( )A、0.1(精确到0.1) B、0.06(精确到百分位) C、0.061(精确到千分位) D、0.0605(精确到0.0001)7. 如图,从①和②的( )方向看到的形状图是一样的.
A、加 B、油 C、子 D、学5. 如果家用电冰箱冷藏室的温度是4℃,冷冻室的温度比冷藏室的温度低22℃,那么冷冻室的温度是( )A、18℃ B、-26℃ C、-22℃ D、-18℃6. 用四舍五入法对0.06045取近似值,错误的是( )A、0.1(精确到0.1) B、0.06(精确到百分位) C、0.061(精确到千分位) D、0.0605(精确到0.0001)7. 如图,从①和②的( )方向看到的形状图是一样的.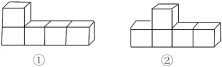 A、正面 B、左面 C、上面 D、左面、上面8. 下列说法正确的是( )A、0既不是整数,也不是分数. B、一个数的绝对值一定是正数. C、一个有理数不是整数,就是分数 D、绝对值等于它本身的数是0和19. 现有①②③④四种型号的铁皮,铁皮的形状与相关尺寸如图所示(单位:dm).从中选两种,正好可以制成一个无盖圆柱形水桶(不计接头),则所选的这两种铁皮的型号是( )
A、正面 B、左面 C、上面 D、左面、上面8. 下列说法正确的是( )A、0既不是整数,也不是分数. B、一个数的绝对值一定是正数. C、一个有理数不是整数,就是分数 D、绝对值等于它本身的数是0和19. 现有①②③④四种型号的铁皮,铁皮的形状与相关尺寸如图所示(单位:dm).从中选两种,正好可以制成一个无盖圆柱形水桶(不计接头),则所选的这两种铁皮的型号是( ) A、①③ B、①④ C、②④ D、②③10. 如图1,点A,B,C是数轴上从左到右排列的三个点,分别对应的数为-5,b,1,某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对应刻度1.8cm,点C对齐刻度5.4cm.则数轴上点B所对应的数b为( )
A、①③ B、①④ C、②④ D、②③10. 如图1,点A,B,C是数轴上从左到右排列的三个点,分别对应的数为-5,b,1,某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对应刻度1.8cm,点C对齐刻度5.4cm.则数轴上点B所对应的数b为( )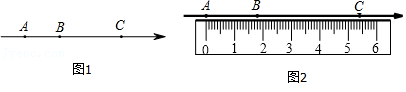 A、-3 B、-2 C、-1 D、3
A、-3 B、-2 C、-1 D、3二、填空题(本大题共6个小题,每小题3分,满分18分)
-
11. “枪打一条线,棍扫一大片”从字面上理解这句话所描述的现象,用数学知识可解释为: .12. 根据央视报道,去年我国汽车尾气排放总量大约为47000000吨.将47000000用科学记数法表示为.13. 用计算器求(-0.802)3的结果,按键次数是14. 某几何体是由若干个大小相同的小正方体组合而成,下面是分别从正面、左面、上面看到的该几何体的形状图,则组成该几何体的小正方体的个数为
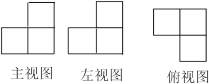 15. 若|a|=4,|b|=2,且a+b的绝对值与它的相反数相等,则a+b的值是16. 如图是一个没有完全剪开的正方体,若再剪开一条棱,则得到的平面展开图不可能是下列图中的 . (填序号)
15. 若|a|=4,|b|=2,且a+b的绝对值与它的相反数相等,则a+b的值是16. 如图是一个没有完全剪开的正方体,若再剪开一条棱,则得到的平面展开图不可能是下列图中的 . (填序号)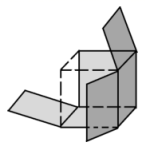

三、解答题(本大题共9个小题,共72分.)
-
17. 计算:(1)、;(2)、 .18. 淇淇在计算:时,步骤如下:
解:原式=-2022-(-6)+6÷-6………………①
=-2022+6+12-18………………………②
=-2048…………………………………③
(1)、淇淇的计算过程中开始出现错误的步骤是 ;(填序号)(2)、请给出正确的解题过程.19. 如图,是由6个大小相同的小正方体块搭建的几何体,其中每个小正方体的棱长为l厘米.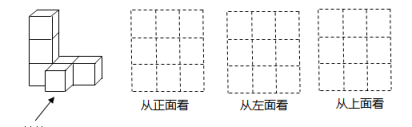 (1)、如果在这个几何体上再添加一些小立方体块,并保持俯视图和左视图不变,最多可以再添加 个小立方块.(2)、请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.20. 画一条数轴,并在数轴上表示:3.5和它的相反数,-2和它的倒数,绝对值等于3的数,并把这些数由小到大用“<”号连接起来.21. 有个填写运算符号的游戏:在“1□2□6□9”中的每个□内,填入“+”“-”“×”“÷”中的某一个(可重复使用),然后计算结果.(1)、若1×2□6-9>0,则填□内的符号为 ;(2)、若使算式1÷2×6□9值最小,请推算□内的符号;(3)、若1-2□6□9=-2,请直接依次写出所有可以填入两个□内的符号.22. 请根据图示的对话解答下列问题.
(1)、如果在这个几何体上再添加一些小立方体块,并保持俯视图和左视图不变,最多可以再添加 个小立方块.(2)、请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.20. 画一条数轴,并在数轴上表示:3.5和它的相反数,-2和它的倒数,绝对值等于3的数,并把这些数由小到大用“<”号连接起来.21. 有个填写运算符号的游戏:在“1□2□6□9”中的每个□内,填入“+”“-”“×”“÷”中的某一个(可重复使用),然后计算结果.(1)、若1×2□6-9>0,则填□内的符号为 ;(2)、若使算式1÷2×6□9值最小,请推算□内的符号;(3)、若1-2□6□9=-2,请直接依次写出所有可以填入两个□内的符号.22. 请根据图示的对话解答下列问题.
求:
(1)、a,b的值;(2)、8-a+b-c的值.23. 如图,是用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个直径2米的半圆.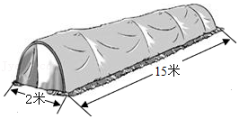 (1)、这个大棚的种植面积是多少平方米?(2)、覆盖在这个大棚上的塑料薄膜约有多少平方米?(3)、大棚内的空间约有多大?24. 阅读以下内容,完成下列题目.
(1)、这个大棚的种植面积是多少平方米?(2)、覆盖在这个大棚上的塑料薄膜约有多少平方米?(3)、大棚内的空间约有多大?24. 阅读以下内容,完成下列题目.小明说:“我定义了一种新的运算,叫❈(加乘)运算.”然后他写出了一些按照❈(加乘)运算的法则进行运算的算式:(+5)❈(+2)=+7;(-3)❈(-5)=+8;(-3)❈(+4)=-7;(+5)❈(-6)=-11;0❈(+8)=|+8|=8;(-6)❈0=|-6|=6.
小颖看了这些算式后说:“我知道你定义的❈(加乘)运算的运算法则了.”
聪明的你也看明白了吗?请完成下列问题:
(1)、请联想回顾有理数运算法则,归纳❈(加乘)运算的运算法则:;(2)、计算:(-2)❈[0❈(-5)]= . (括号的作用同在有理数运算中的作用)(3)、我们知道加法有交换律和结合律,请你判断加法交换律在❈(加乘)运算中是否适用?并举例验证.25. 一辆公交车从起点站开出后,途中经过6个停靠站,最后到达终点站.下表记录了这辆公交车全程载客变化情况,其中正数表示上车人数,负数表示下车的人数.停靠
站
起点站
中间
第1站
中间
第2站
中间
第3站
中间
第4站
中间
第5站
中间
第6站
终点
站
上下车
人数
+21
-3
+7
-6
+5
0
+1
-4
+3
-9
+6
-7
0
-14
(1)、中间第4站上车人数是 人,下车人数是 人;(2)、中间的6个站中,第 站没有人上车,第 站没有人下车;(3)、中间第2站开车时车上人数是 人,中间第五站到站时车上的人数 ;(4)、若每人乘坐一次公交车费用为1元,那么,该公交车本次从起点站至终点站共收费多少元?(5)、请自己提出一个合理的问题,并进行解答。