浙江省杭州市余杭区2022-2023学年八年级上学期期中数学试卷
试卷更新日期：2022-11-14 类型：期中考试
一、选择题：本大题有10个小题，每小题3分，共30分．
-
1. 三角形的两边分别为6，10，则第三边的长可能等于（ ）A、3 B、11 C、16 D、172. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
3. 工人师傅砌门时，常用一根木条固定长方形门框，使其不变形，这样做的根据是（ ）A、两点之间的线段最短 B、三角形具有稳定性 C、长方形是轴对称图形 D、长方形的四个角都是直角4. 直角三角形两直角边长度为5，12，则斜边上的高（ ）A、6 B、8 C、13 D、5. 如图，△ABC≌△A'B'C，其中∠A=36°，∠C=24°，则∠B'=（ ）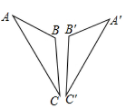
A、60° B、100 C、120 D、135°6. 下列命题的逆命题是真命题的是（ ）A、如果两个角是直角，那么它们相等 B、全等三角形的对应角相等 C、两直线平行，内错角相等 D、对顶角相等7. 如图，A，P是直线m上的任意两个点，B，C是直线n上的两个定点，且直线m∥n.则下列说法正确的是（ ）
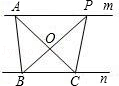A、AC=BP B、△ABC的周长等于△BCP的周长 C、△ABC的面积等于△ABP的面积 D、△ABC的面积等于△PBC的面积8. 如图，AD是等腰△ABC底边BC边上的中线，BE 平分∠ABC，交AD于点E，AC=12，DE=3，则△ABE 的面积是（ ）
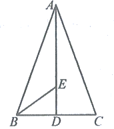A、16 B、18 C、32 D、369. 如图，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则MC2-MB2等于（ ）
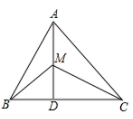A、9 B、35 C、45 D、无法计算10. 如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是AC边上一点．若AE=2，EM+CM的最小值为（ ）
A、2 B、4 C、3 D、1+2二、填空题：本题有6个小题，每小题4分，共24分．
-
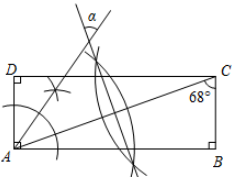
11. 等腰三角形的两条边长为2，4，则等腰三角形的周长为12. 命题“等腰三角形两底角相等”的逆命题是 ， 这个逆命题是命题(填"真”或“假”)。13. 如图，依据尺规作图的痕迹，计算 ．
14. 如图，△ABC中，AB=4，BC=5，CA=6，三条角平分线交于点O．△CAO的面积等于9，则△ABO的面积= ．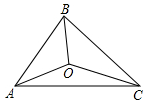
15. 如图，在四边形 中， ， ， ， 、 分别是对角线 、 的中点，则 .
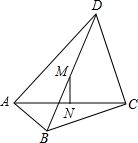16. 如图，在△ABC中，∠A=90°，∠B=38°，点E，F分别在边BC，AC上，将△CEF沿EF所在的直线折叠，使C的对应点C'落在AB上，且CE=BC"，则∠AFC'= ．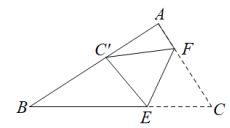
三、解答题：本题有7小题，共66分．
-
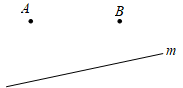
17. 如图，直线m表示一条公路，A，B表示两所大学，要在公路旁修建一个车站P，使车站到两所大学的距离相等．请用尺规在图上找出点P并说明理由．
18. 如图，点D在AB上，点E在AC上，BE ， CD相交于点O.已知∠A=50°，∠BOD=70°，∠C=30°，求∠B的度数.
19. 已知：如图，在△ADF和△BCE中，点B，F，E，D依次在一条直线上，若AF∥CE，∠B=4D，BF=DE，求证：AF=CE．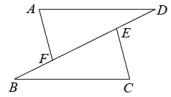
20. 如图，在△ABC中，AB=AC，CD⊥AB于点D，过点D作DE⊥BC于点E，交CA的延长线于点F．
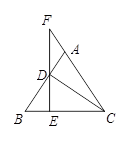(1)、求证：△ADF是等腰三角形．(2)、当CD 8，CF=10时，求BD的长．21. 如图，△ABC中，∠C=2∠B，D是BC上一点，且AD⊥AB，点E是BD的中点，连接AE．
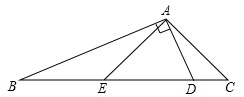(1)、求证：BD=2AC；(2)、若AE=6.5，AD=5，那么△ABE的周长是多少？22. 如图，点O是等边△ABC内一点，∠AOB=100°，∠BOC=α．以OC为边作等边△OCD，连接AD．
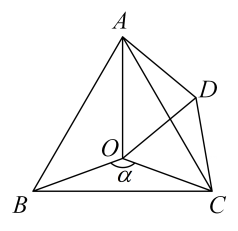(1)、求证：△BOC≌△ADC；(2)、当a=150°时，试判断△AOD的形状，并说明理由；(3)、探究：当α为多少度时，△AOD是等腰三角形？23. 已知：△ACD和△BCE都是等腰直角三角形，∠ACD=∠BCE=90°．
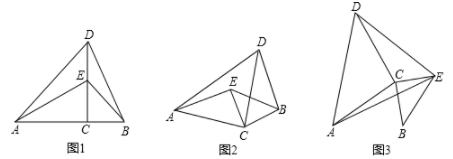(1)、如图1，点A，C，B在同一条直线上，点E在CD上时，连接AE，BD．线段AE与BD的数量关系是 ， 位置关系是 ． (直接写出答案)(2)、如图2，逆时针旋转△BCE，连接AE，BD，题(1)中的结论是否仍然成立？请说明理由；(3)、如图3，顺时针旋转△BCE，连接AE，DE．若有AE2=DE2+2CE2 ， 求∠DEC的度数．