浙江省杭州市临平区2022-2023学年九年级上学期数学期中检测
试卷更新日期：2022-11-14 类型：期中考试
一、选择题：本题有10个小题，每小题3分，共30分。
-
1. 下列图形中既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 抛物线y=-(x-1)2+3的顶点坐标是（ ）A、(1，3) B、(-1，3) C、(-1，-3) D、(1，-3)3. 任意抛掷一枚均匀的骰子，骰子停止转动后，发生可能性最大的事件是（ ）A、朝上一面的点数大于2 B、朝上一面的点数为3 C、朝上一面的点数是2的倍数 D、朝上一面的点数是3的倍数4. 若⊙O的半径为3，点A到圆心O的距离为2，则点A与⊙O的位置关系为（ ）A、点A在圆外 B、点A在圆上 C、点A在圆内． D、不能确定5. 下列事件是必然事件的是（ ）A、相等的圆心角所对的弧相等 B、三点确定一个圆 C、抛掷一枚骰子，朝上面的点数小于6 D、事件发生的概率是I6. 若二次函数y=ax2(a≠0)的图象过点(-2，-3)，则必在该图象上的点还有（ ）A、(-3，-2) B、(2，3) C、(2，-3) D、(-2，3)7. 已知(-3，y1)，(-2，y2)，(1，y3)是二次函数y=-2x2-8x+m图象上的点，则（ ）A、y2>y1>y3 B、y2>y3>y1 C、y1<y2<y3 D、y3<y2<y18. 如图，已知点A，B，C依次在⊙o上，∠B-∠A=40°，则∠AOB的度数为（ ）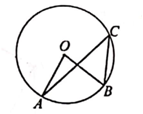
A、84° B、80° C、72° D、70°9. 抛物线y=a2+bx+c(a≠0)如图所示，对称轴是直线x=1，下列结论：①a-b+c<0；②a+b>0；③a+b≥ax2+bx； ④4ac<b2中正确的个数是（ ）
A、1个 B、2个 C、3个 D、4个10. 已知，二次函数y=ax2+bx-1(a，b是常数，a≠0)的图象经过A(2，1)，B(4，3)，C(4，-1)三个点中的其中两个点，平移该函数的图象，使其顶点始终在直线y=x-1上，则平移后所得抛物线与y轴交点纵坐标的（ ）A、最大值为-1 B、最小值为-1 C、最大值为 D、最小值为二、填空题：本题有6个小题，每小题4分，共24分．
-
11. 将函数y=(x+1)2的图象向右平移2个单位，再向上平移1个单位得到函数图象的表达式为。12. 甲、乙、丙三个人相互传一个球，由甲开始发球，并作为第一次传球，则经过两次传球后，球回到甲手中的概率是。13. 如图，BD、CE是⊙O的直径，弦AE∥BD，AD交CE于点F，∠A=25°，则∠AFC=
14. 已知点A(0，3)，点B(2，3)是抛物线y=-x2+bx+c上两点，则该二次函数的最值是。15. 如图，点A，B，C，D，E都是⊙O上的点，AC=AE，∠D=128°，则∠B=°。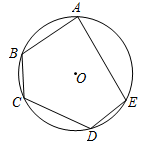
16. 已知二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如表：x
……
0
1
2
3
……
y
……
5
2
1
2
……
若A(m，y1)， B(m+6，y2)两点都在该函数图象上，当y1>y2时，m的取值范围是。
三、解答题：本题有7个小题，共66分．
-
17. 如图，已知正方形ABCD，点E在AB边上，点F在BC边的延长线上，且CF=AE．以图中某一点为旋转中心，将△DAE按逆时针方向旋转一定角度后恰好与△DCF重合．
(1)、旋转中心是点 ， 旋转角的度数为°．(2)、判断△DFE的形状并说明理由18. 已知：如图， 中弦 .求证： .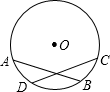
19. 一个不透明的布袋中装有3个只有颜色不同的球，其中1个黄球、2个红球.(1)、任意摸出1个球，记下颜色后不放回，再任意摸出1个球，求两次摸出的球恰好都是红球的概率（要求画树状图或列表）；(2)、现再将n个黄球放入布袋，搅匀后，使任意摸出1个球是黄球的概率为 ，求n的值.20. 二次函数的图象经过点A(2，0)，B(3，0)，C(1，6)．(1)、求二次函数解析式；(2)、求当y>4时，自变量x的取值范围．21. 如图，AB是⊙O的直径，点C，D是⊙O上的点，且OD∥BC，AC分别与BD，OD相交于点E，F．
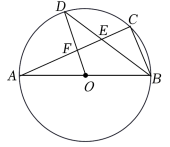(1)、求证：点D为的中点；(2)、若DF=4，AC=16，求⊙O的直径．22. 某公园对一块长 20m，宽10m的场地进行设计，方案如图所示．阴影区域为绿化区(四块全等的矩形)，空白区域为活动区，且4个出口宽度相同，其宽度不小于4m，不大于8m．设出口长均为x(m)，活动区面积为y(m)．
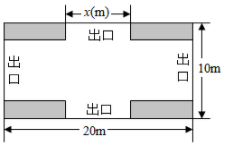(1)、求y关于x的函数表达式：(2)、当x取多少时，活动区面积最大？最大面积是多少？(3)、若活动区布置成本为10元/m2 ， 绿化区布置成本为8元/m2 ， 布置场地的预算不超过1850元，当x为整数时，请求出符合预算且使活动区面积最大的x值及此时的布置成本．23. 已知二次函数y=ax2+4ax+3a(a为常数)．(1)、若二次函数的图象经过点(2，3)，求函数y的表达式，：(2)、若a>0，当x<时，此二次函数y随着x的增大而减小，求m的取值范围，(3)、若二次函数在-3≤x≤1时有最大值3，求a的值．