浙江省宁波市镇海区蛟川书院2022-2023学年八年级上学期期中数学试卷
试卷更新日期:2022-11-14 类型:期中考试
一、选择题(共10小题,每小题4分,共40分)
-
1. 奥运火炬时隔14年再次在“鸟巢”点燃,北京由此成为世界上首个既举办夏季奥运会又举办冬季奥运会的“双奥之城”,下列各届冬奥会会徽图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若x>y,则下列式子中错误的是( )A、x-2>y-2 B、x+2>y+2 C、-2x>-2y D、>3. 点M(1,2)关于x轴对称点的坐标为( )A、(-1,2) B、(-1,-2) C、(2,-1) D、(1,-2)4. 下列长度的三条线段,能组成三角形的是( )A、3,5,7 B、3,6,10 C、5,5,11 D、5,6,115. 已知(-3,y1) (-1,y2),( , y3)是直线y=x+2上的三个点,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y3>y2>y1 C、y1>y3>y2 D、y3>y1>y26. 某次知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分.小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对的题数是( )A、15 B、16 C、17 D、187. 若一次函数 ( 都是常数)的图象经过第一、二、四象限,则一次函数 的图象大致是( )A、
2. 若x>y,则下列式子中错误的是( )A、x-2>y-2 B、x+2>y+2 C、-2x>-2y D、>3. 点M(1,2)关于x轴对称点的坐标为( )A、(-1,2) B、(-1,-2) C、(2,-1) D、(1,-2)4. 下列长度的三条线段,能组成三角形的是( )A、3,5,7 B、3,6,10 C、5,5,11 D、5,6,115. 已知(-3,y1) (-1,y2),( , y3)是直线y=x+2上的三个点,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y3>y2>y1 C、y1>y3>y2 D、y3>y1>y26. 某次知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分.小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对的题数是( )A、15 B、16 C、17 D、187. 若一次函数 ( 都是常数)的图象经过第一、二、四象限,则一次函数 的图象大致是( )A、 B、
B、 C、
C、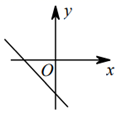 D、
D、 8. 如图,折叠直角三角形纸片ABC,使得点A,B都与斜边AB上的点F重合,折痕分别为DE和GH.则下列结论不一定成立的是( )
8. 如图,折叠直角三角形纸片ABC,使得点A,B都与斜边AB上的点F重合,折痕分别为DE和GH.则下列结论不一定成立的是( ) A、DH=AB B、EF=FG C、EF⊥FG D、DE∥GH9. 如图,在平面直角坐标系中,0为坐标原点,A点坐标(6,0),B点坐标(3,-3),动点P从A点出发,沿x轴正方向运动,连接BP,以BP为直角边向下作等腰直角三角形BPC,∠PBC=90°,连结OC,当OC=10时,△OCP的面积为( )
A、DH=AB B、EF=FG C、EF⊥FG D、DE∥GH9. 如图,在平面直角坐标系中,0为坐标原点,A点坐标(6,0),B点坐标(3,-3),动点P从A点出发,沿x轴正方向运动,连接BP,以BP为直角边向下作等腰直角三角形BPC,∠PBC=90°,连结OC,当OC=10时,△OCP的面积为( ) A、16 B、64 C、32 D、3610. 如图,在Rt△ABC中,∠ACB=90°,分别以AB,AC,BC为斜边作三个等腰直角△ABD,△ACE,△BCF,图中阴影部分的面积分别记为S1 , S2 , S3 , S4 , 若已知Rt△ABC的面积,则下列代数式中,一定能求出确切值的代数式是( )
A、16 B、64 C、32 D、3610. 如图,在Rt△ABC中,∠ACB=90°,分别以AB,AC,BC为斜边作三个等腰直角△ABD,△ACE,△BCF,图中阴影部分的面积分别记为S1 , S2 , S3 , S4 , 若已知Rt△ABC的面积,则下列代数式中,一定能求出确切值的代数式是( ) A、S4 B、S1+S4-S3 C、S2+S3+S4 D、S1+S2-S3
A、S4 B、S1+S4-S3 C、S2+S3+S4 D、S1+S2-S3二、填空题(共6小题,每小题5分,共30分)
-
11. “x的2倍减去1是负数”用不等式表示为 .12. 若点A(-5,m),B(n,4)都在函数y=x+b的图象上,则m+n的值为。13. 若关于x的一元一次不等式组无解,则a的取值范围是。14. 如图,在Rt△ABC中,∠ACB=90°,AC=5,D为AB的中点,BE⊥CD交CD的延长线于E,若BE=4,则AB=。
 15. 如图,已知在中, , 点D是边上的任意一点,以为折痕翻折 , 使点B落在点E处,连接 , 当为直角三角形时,的长为 .
15. 如图,已知在中, , 点D是边上的任意一点,以为折痕翻折 , 使点B落在点E处,连接 , 当为直角三角形时,的长为 . 16. 如图,在Rt△ABC中,∠ACB=90°,AB=6,BC=4,D,E分别是AC,AB上的动点,且AD=BE,连结BD,CE,则BD+CE的最小值为。
16. 如图,在Rt△ABC中,∠ACB=90°,AB=6,BC=4,D,E分别是AC,AB上的动点,且AD=BE,连结BD,CE,则BD+CE的最小值为。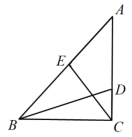
三、解答题(共8小题,共80分)
-
17.(1)、解不等式:x+2-3(x+1)>1(2)、解不等式组18. 已知一次函数图象经过(3,5)和(-4,-9)两点,(1)、求此一次函数解析式:(2)、若点(a,2)在函数图象上,求a的值。19. 如图①、图②是6X6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹.
 (1)、在图①中的线段AB上找一点D,连结CD,使∠BCD=∠BDC.(2)、在图②中的线段AC上找一点E,连结BE,使∠ABE=∠BAE.20. 如图,直线AB与x轴相交于点A,与y轴相交于点B(0,4),点C(-2,6)在直线AB上,连结OC.
(1)、在图①中的线段AB上找一点D,连结CD,使∠BCD=∠BDC.(2)、在图②中的线段AC上找一点E,连结BE,使∠ABE=∠BAE.20. 如图,直线AB与x轴相交于点A,与y轴相交于点B(0,4),点C(-2,6)在直线AB上,连结OC. (1)、求直线AB对应的函数表达式和OBC的面积;(2)、点P为直线AB上一动点,AOP的面积与OBC的面积相等,求点P的坐标.21. 如图,△ABC中,AB=AC,D在AB上,又在AC的中垂线上,点E在CD的延长线上,点F在AC上,AF=CE.
(1)、求直线AB对应的函数表达式和OBC的面积;(2)、点P为直线AB上一动点,AOP的面积与OBC的面积相等,求点P的坐标.21. 如图,△ABC中,AB=AC,D在AB上,又在AC的中垂线上,点E在CD的延长线上,点F在AC上,AF=CE.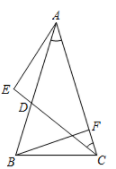 (1)、求证:△ABF≌△CAE.(2)、若CD平分∠ACB,求∠EAD+∠FBC的度数.22. 习近平总书记说:“人民群众多读书,我们的民族精神就会厚重起来、深邃起来.”某书店计划在4月23日世界读书日之前,同时购进A,B两类图书,已知购进3本A类图书和4本B类图书共需288元;购进6本A类图书和2本B类图书共需306元.(1)、A,B两类图书每本的进价各是多少元?(2)、该书店计划用4500元全部购进两类图书,设购进A类x本,B类y本.
(1)、求证:△ABF≌△CAE.(2)、若CD平分∠ACB,求∠EAD+∠FBC的度数.22. 习近平总书记说:“人民群众多读书,我们的民族精神就会厚重起来、深邃起来.”某书店计划在4月23日世界读书日之前,同时购进A,B两类图书,已知购进3本A类图书和4本B类图书共需288元;购进6本A类图书和2本B类图书共需306元.(1)、A,B两类图书每本的进价各是多少元?(2)、该书店计划用4500元全部购进两类图书,设购进A类x本,B类y本.①求y关于x的关系式;
②进货时,A类图书的购进数量不少于60本,已知A类图书每本的售价为38元,B类图书每本的售价为50元,求如何进货才能使书店所获利润最大,最大利润为多少元?
23. 如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上的一点,将△BCD绕点C逆时针旋转90°得到OACE,易得△BCD≌△ACE,连结BE.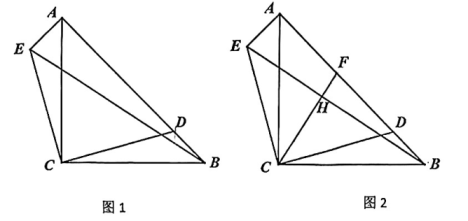 (1)、求∠BCE+∠ACD的度数.(2)、当BC=5,BD=时,求BE、CE的长.(3)、如图2,在(2)的条件下,取AD中点E连结CF交BE于H,试探究线段BE、CF的数量关系和位置关系,并说明理由.24. 如图1, 在平面直角坐标系中,一次函数y=x+4与x轴交于点B,与y轴交于点A,点C为线段AB的中点,过点C作DC⊥x轴,垂足为D.
(1)、求∠BCE+∠ACD的度数.(2)、当BC=5,BD=时,求BE、CE的长.(3)、如图2,在(2)的条件下,取AD中点E连结CF交BE于H,试探究线段BE、CF的数量关系和位置关系,并说明理由.24. 如图1, 在平面直角坐标系中,一次函数y=x+4与x轴交于点B,与y轴交于点A,点C为线段AB的中点,过点C作DC⊥x轴,垂足为D.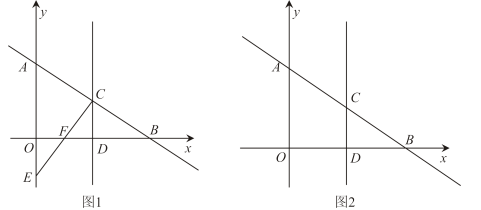 (1)、求A、B两点的坐标;(2)、若点E为y轴负半轴上一点,连接CE交x轴于点F,且CF=FE,在直线CD上有一点P,使得AP+EP最小,求P点坐标;(3)、如图2,直线CD上是否存在点Q使得∠ABQ=45°,若存在,请求出点Q的坐标,若不存在,请说明理由.
(1)、求A、B两点的坐标;(2)、若点E为y轴负半轴上一点,连接CE交x轴于点F,且CF=FE,在直线CD上有一点P,使得AP+EP最小,求P点坐标;(3)、如图2,直线CD上是否存在点Q使得∠ABQ=45°,若存在,请求出点Q的坐标,若不存在,请说明理由.