安徽省皖豫名校联盟2021-2022学年高一上学期数学期中联考试卷

试卷更新日期：2022-11-14 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x < 2} ， B = {x | x^{2} - 3 x + 2 < 0}$ ，则（）

A、 $A ⊆ B$ B、 $A \cap B = \emptyset$ C、 $B ⊆ A$ D、 $A \cup B = R$

查看试题解析
2. 设 $a$ ， $b \in R$ ，则“ $a < b$ ”是“ $(a - b) a^{2} < 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 下列各组函数中， $f (x)$ 与 $g (x)$ 表示同一函数的是（）

A、 $f (x) = x ， g (x) = \sqrt{x^{2}}$ B、 $f (x) = 1 ， g (x) = (x - 1)^{0}$ C、 $f (x) = \frac{(\sqrt{x})^{2}}{x} ， g (x) = \frac{x}{(\sqrt{x})^{2}}$ D、 $f (x) = \frac{x^{2} - 9}{x + 3} ， g (x) = x - 3$

查看试题解析
4. 函数 $f (2 x)$ 的定义域为 $[0 ， 1)$ ，则 $f (1 - 3 x)$ 的定义域是（）

A、 $(- 2 ， 1]$ B、 $(- \frac{1}{2} ， 1]$ C、 $(- \frac{1}{3} ， \frac{1}{3}]$ D、 $(- 2 ， 4]$

查看试题解析
5. 十六世纪中叶，英国数学家雷科德在《砺智石》一书中首先把“ $=$ ”作为等号使用，后来英国数学家哈利奥特首次使用“ $<$ ”和“ $>$ ”符号，并逐渐被数学界接受，不等号的引入对不等式的发展影响深远.若 $a, b, c \in R$ ，则下列命题正确的是（）.

A、若 $a b \neq 0$ 且 $a < b$ ，则 $\frac{1}{a} > \frac{1}{b}$ B、若 $0 < a < 1$ ，则 $a^{3} < a$ C、若 $a > b > 0$ ，则 $\frac{b + 1}{a + 1} < \frac{b}{a}$ D、若 $c < b < a$ 且 $a c < 0$ ，则 $c b^{2} < a b^{2}$

查看试题解析
6. 函数 $y = \frac{2 x^{3}}{2^{x} + 2^{- x}}$ 在 $[- 6 ， 6]$ 的图像大致为（）

A、 B、 C、 D、

查看试题解析
7. 已知函数 $f (x) = (m^{2} - m - 1) x^{m^{2} - 2 m - 2}$ 是幂函数，且在 $(0 ， + ∞)$ 上是减函数，则实数 $m =$ （）

A、2 B、 $- 1$ C、4 D、2或 $- 1$

查看试题解析
8. 已知 $a > 0$ ， $b > 0$ ，如果不等式 $\frac{2}{a} + \frac{1}{b} \geq \frac{m}{2 a + b}$ 恒成立，那么 $m$ 的最大值等于（）

A、7 B、8 C、9 D、10

查看试题解析
9. 已知函数 $f (x) = {\begin{array}{l} (2 - \frac{a}{2}) x + 2 ， x \leq 2 \\ a^{x - 1} ， x > 2 \end{array}$ 在 $R$ 上是增函数，则实数 $a$ 的取值范围是（）

A、 $2 < a < 4$ B、 $2 \leq a < 4$ C、 $3 < a < 4$ D、 $3 \leq a < 4$

查看试题解析
10. 食品安全问题越来越引起人们的重视，农药、化肥的滥用给人民群众的健康带来了一定的危害．为了给消费者带来放心的蔬菜，某农村合作社每年投入资金200万元，搭建甲、乙两个无公害蔬菜大棚，每个大棚至少要投入资金40万元，其中甲大棚种西红柿，乙大棚种黄瓜．根据以往的种菜经验，发现种西红柿的年收入P（单位：万元）、种黄瓜的年收入Q（单位：万元）与各自的投入资金 $a_{1}$ ， $a_{2}$ （单位：万元）满足 $P = 80 + 4 \sqrt{2 a_{1}}$ ， $Q = \frac{1}{4} a_{2} + 120$ ．设甲大棚的投入资金为x（单位：万元），每年两个大棚的总收入为 $f (x)$ （单位：万元），则总收入 $f (x)$ 的最大值为（）

A、282万元 B、228万元 C、283万元 D、229万元

查看试题解析
11. 函数 $f (x) = x (| x | - 1)$ 在 $[m ， n]$ 上的最小值为 $- \frac{1}{4}$ ，最大值为2，则 $n - m$ 的最大值为（）

A、 $\frac{5}{2}$ B、 $\frac{5}{2} + \frac{\sqrt{2}}{2}$ C、 $\frac{3}{2}$ D、2

查看试题解析
12. 已知定义在R上的连续奇函数 $f (x)$ 满足 $f (x - 4) = - f (x)$ ，且在区间 $[0 ， 2]$ 上单调递增，下列说法正确的个数为（）
①函数 $f (x)$ 的图象关于直线 $x = 4 k - 6 (k \in Z)$ 对称
②函数 $f (x)$ 的单调递增区间为 $[8 k - 6 ， 8 k - 2] (k \in Z)$
③函数 $f (x)$ 在区间 $[- 2021 ， 2021]$ 上恰有1010个最值点
④若关于x的方程 $f (x) - m = 0$ 在区间 $[- 8 ， 8]$ 上有根，则所有根的和可能为0或 $\pm 4$ 或 $\pm 8$

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 命题“ $\forall x \in [0 ， + \infty) ， x^{3} + x \geq 0$ ”的否定是.

查看试题解析
14. 函数 $f (x) = \sqrt{m x^{2} - 2 x + 1}$ 的定义域为R，则实数m的取值范围是.

查看试题解析
15. 设函数 $y = f (x)$ 为定义在R上的奇函数，当 $x \geq 0$ 时， $f (x) = 2^{x} + 2 x + b (b \in R)$ ，则 $x < 0$ 时， $y = f (x)$ 的解析式为.

查看试题解析
16. 设函数 $f (x)$ 的定义城为D，如果存在正实数k，使对任意的 $x \in D$ ，都有 $x + k \in D$ ，且 $f (x + k) > f (x)$ 恒成立，则称函数 $f (x)$ 为D上的“k型增函数”.已知 $f (x)$ 是定义在R上的奇函数，且当 $x > 0$ 时， $f (x) = | x - a | - 2 a$ ，若 $f (x)$ 为R上的“2021型增函数”，则实数a的取值范围是.

查看试题解析

三、解答题

17. 已知 $A = {x | a \leq x \leq a + 3}$ ， $B = {x | - x^{2} + 4 x + 5 < 0}$ .

(1)、若 $a = - 3$ ，求 $A \cap B$ ；

(2)、若 $x \in A$ 是 $x \in ∁_{R} B$ 的充分不必要条件，求实数 $a$ 的取值范围.

查看试题解析
18. 已知函数 $f (x) = a x^{2} + x + c$ 满足：① $f (x - \frac{1}{2}) = f (- x)$ ；②关于x的不等式 $f (x) < 0$ 的解集是 $(m ， 1) (m < 1)$ .

(1)、求函数 $f (x)$ 的解析式；

(2)、求函数 $g (x) = f (x) + (4 k + 3) x (k \in R)$ 在 $[1 ， 3]$ 上的最小值.

查看试题解析
19. 如图，长方形 $A B C D$ 表示一张 $6 \times 12$ （单位：分米）的工艺木板，其四周有边框（图中阴影部分），中间为薄板.木板上一瑕疵（记为点P）到外边框 $A B ， A D$ 的距离分别为1分米，2分米.现欲经过点P锯掉一块三角形废料 $M A N$ ，其中M，N分别在 $A B ， A D$ 上.设 $A M ， A N$ 的长分别为m分米，n分米.

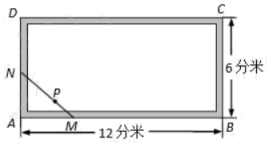(1)、求 $\frac{2}{m} + \frac{1}{n}$ 的值；

(2)、为使剩下木板 $M B C D N$ 的面积最大，试确定m，n的值；

(3)、求剩下木板 $M B C D N$ 的外边框长度（ $M B ， B C ， C D ， D N$ 的长度之和）的最大值及取得最大值时m，n的值.

查看试题解析
20. 若函数 $f (x) = a \cdot 4^{x} - 2 a \cdot 2^{x} + 1 - b (a > 0)$ 在区间 $[1 ， 2]$ 上的最大值为9，最小值为1.

(1)、求a，b的值；

(2)、若方程 $f (x) - k \cdot 2^{x} = 0$ 在 $[- 1 ， 2]$ 上有两个不同的解，求实数k的取值范围.

查看试题解析
21. 已知定义在 $(0 ， + \infty)$ 上的函数 $f (x)$ 满足：①对任意的 $x ， y \in (0 ， + \infty)$ ，都有 $f (x y) = f (x) + f (y)$ ；②当且仅当 $x > 1$ 时， $f (x) < 0$ 成立.

(1)、求 $f (1)$ ；

(2)、判断 $f (x)$ 在 $(0 ， + \infty)$ 上的单调性，并予以证明；

(3)、若对任意的 $x \in [- 1 ， 1]$ ，不等式 $f (3^{2 x} + 3^{- 2 x}) \leq f [m (3^{x} + 3^{- x}) - 10]$ 恒成立，求实数m的取值范围.

查看试题解析
22. 我们知道，函数 $y = f (x)$ 的图象关于坐标原点成中心对称的充要条件是函数 $y = f (x)$ 为奇函数，有同学发现可以将其推广为：函数 $y = f (x)$ 的图象关于点 $P (a ， b)$ 成中心对称的充要条件是函数 $y = f (x + a) - b$ 为奇函数.

(1)、依据推广结论，求函数 $f (x) = x^{3} - 3 x^{2}$ 图象的对称中心；

(2)、请利用函数 $f (x) = x^{3} - 3 x^{2}$ 的对称性求 $f (- 2019) + f (- 2017) + f (- 2015) + \cdot \cdot \cdot f (- 3) + f (- 1) + f (1) + f (3) + f (5) + \cdot \cdot \cdot f (2017) + f (2019) + f (2021)$ 的值；

(3)、类比上述推广结论，写出“函数 $y = f (x)$ 的图象关于x轴成轴对称的充要条件是函数 $y = f (x)$ 为偶函数”的一个推广结论.（不需要证明）

查看试题解析