吉林省白城市通榆县2022-2023学年第一学期九年级第二次阶段考试数学试题
试卷更新日期:2022-11-14 类型:期中考试
一、单项选择题(每小题2分,共12分)
-
1. 2022年4月16日,神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园。六个月的飞天之旅展现了中国航天科技的新高度.下列航天图标,其文字上方的图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若关于x的方程x2+4x+c=0有两个相等的实数根,则c的值是( )A、4 B、-4 C、16 D、-163. 如图,四边形ABCD内接于⊙O,∠BAD=70°,则∠BCD的度数是( )
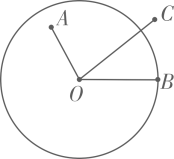
2. 若关于x的方程x2+4x+c=0有两个相等的实数根,则c的值是( )A、4 B、-4 C、16 D、-163. 如图,四边形ABCD内接于⊙O,∠BAD=70°,则∠BCD的度数是( )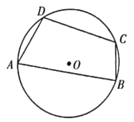 A、90° B、100° C、110° D、120°4. 如图,OA、OB是⊙O的两条半径,点C在⊙O上,若∠AOB=80°,则∠ACB的度数为( )
A、90° B、100° C、110° D、120°4. 如图,OA、OB是⊙O的两条半径,点C在⊙O上,若∠AOB=80°,则∠ACB的度数为( ) A、30° B、40° C、50° D、60°5. 已知函数y=ax2+bx+3的图象如图所示,则a,b的值可能是( )
A、30° B、40° C、50° D、60°5. 已知函数y=ax2+bx+3的图象如图所示,则a,b的值可能是( ) A、a=1,b=2 B、a=1,b=-2 C、a=-1,b=2 D、a=-1,b=-26. 2022年北京冬奥会女子冰壶比赛,有若干支队伍参加了单循环比赛(每两队之间都赛一场),单循环比赛共进行了45场,共有多少支队伍参加比赛?设共有x支队伍参加比赛,则所列方程为( )A、x(x+1)=45 B、=45 C、x(x-1)=45 D、=45
A、a=1,b=2 B、a=1,b=-2 C、a=-1,b=2 D、a=-1,b=-26. 2022年北京冬奥会女子冰壶比赛,有若干支队伍参加了单循环比赛(每两队之间都赛一场),单循环比赛共进行了45场,共有多少支队伍参加比赛?设共有x支队伍参加比赛,则所列方程为( )A、x(x+1)=45 B、=45 C、x(x-1)=45 D、=45二、填空题(每小题3分,共24分)
-
7. 一元二次方程x2-1=0的两根分别为 。8. 点M(1,-2)关于原点对称的点的坐标是。9. 若x=1是一元二次方程x2-2x+m=0的根,则m的值为。10. 抛物线y=2(x+2)2的顶点坐标是 。11. 如图,在⊙O中,点A在圆内,点B在圆上,点C在圆外,若OA=3,OC=5,则OB的长度可能为(写出一个即可)
 12. 如图,将矩形ABCD绕点A顺时针旋转35°,得到矩形AB'C'D',则∠a=°。
12. 如图,将矩形ABCD绕点A顺时针旋转35°,得到矩形AB'C'D',则∠a=°。 13. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法所作EF将矩形窗框ABCD分为上、下两部分,其中E为边AB的黄金分割点,即BE2=AE·AB,已知AB为2米,则线段BE的长为米(结果保留根号).
13. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法所作EF将矩形窗框ABCD分为上、下两部分,其中E为边AB的黄金分割点,即BE2=AE·AB,已知AB为2米,则线段BE的长为米(结果保留根号). 14. 如图,点B,E在半圆O上,四边形OABC,四边形ODEF均为矩形.若AB=3,BC=4,则DF的长为。
14. 如图,点B,E在半圆O上,四边形OABC,四边形ODEF均为矩形.若AB=3,BC=4,则DF的长为。
三、解答题(每小题5分,共20分)
-
15. 解方程:x2-4x-8=0.16. 已知关于x的一元二次方程x2+3x+k-2=0有实数根,求实数k的取值范围。17. 如图,在Rt△ABC中,∠BAC=90°,AB=AC.点D是△ABC内的一点,连接AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连接BD、CE.求证:BD=CE.
 18. 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=-5t2+20t,求小球飞行高度达到最高时的飞行时间.
18. 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=-5t2+20t,求小球飞行高度达到最高时的飞行时间.
四、解答题(每小题7分,共28分)
-
19. 图①、图②都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段AB的端点均在格点上,请在给定的网格中分别按要求画图.
 (1)、在图①中,找一个格点C,使以点A,B,C为顶点的三角形是等腰三角形.(2)、在图②中,找两个格点D,E,使以点A,B,D,E为顶点的四边形是中心对称图形.20. 如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)、在图①中,找一个格点C,使以点A,B,C为顶点的三角形是等腰三角形.(2)、在图②中,找两个格点D,E,使以点A,B,D,E为顶点的四边形是中心对称图形.20. 如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°. (1)、求∠DAB的大小.(2)、若AD=6,则圆心O到BD的距离为。21. 石拱桥是我国古化人民勤劳和w放的结品(如图①),隋化建造的赵州桥览今约有1400年的历史,是我国古代石拱桥的代表,如图②是根据某石供桥的实物图两出的几何图形,桥的主桥拱是圆弧形,表示为 , 桥的跨度(弧所对的弦长)AB=26m,设所在圆的圆心为O,半径OC⊥AB,重足为点D,拱高(弧的中点到弦的距离)CD=5m,连接OB.
(1)、求∠DAB的大小.(2)、若AD=6,则圆心O到BD的距离为。21. 石拱桥是我国古化人民勤劳和w放的结品(如图①),隋化建造的赵州桥览今约有1400年的历史,是我国古代石拱桥的代表,如图②是根据某石供桥的实物图两出的几何图形,桥的主桥拱是圆弧形,表示为 , 桥的跨度(弧所对的弦长)AB=26m,设所在圆的圆心为O,半径OC⊥AB,重足为点D,拱高(弧的中点到弦的距离)CD=5m,连接OB. (1)、直接写出AD与BD的数量关系,(2)、求这座石拱桥主桥拱的半径,(结果精确到1m)22. 如图,隧道的截面由抛物线APB和矩形AMNB构成,矩形的长MN为8m,宽AM为2m,以MN所在的直线为x轴,线段AB的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点P到坐标原点O的距离为6m.
(1)、直接写出AD与BD的数量关系,(2)、求这座石拱桥主桥拱的半径,(结果精确到1m)22. 如图,隧道的截面由抛物线APB和矩形AMNB构成,矩形的长MN为8m,宽AM为2m,以MN所在的直线为x轴,线段AB的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点P到坐标原点O的距离为6m. (1)、求抛物线的解析式.(2)、如果该隧道内设双行道,现有一辆货运卡车高4.2m,宽2.4m,这辆货运卡车能否通过该隧道?通过计算说明你的结论.
(1)、求抛物线的解析式.(2)、如果该隧道内设双行道,现有一辆货运卡车高4.2m,宽2.4m,这辆货运卡车能否通过该隧道?通过计算说明你的结论.五、解答题(每小题8分,共16分)
-
23. 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为点E,延长BA交⊙O于点F.
 (1)、求证:DE是⊙O的切线.(2)、若DE=2,AF=3,直接写出AE的长.24. 阅读与思考:下面是小明同学的数学小论文,请仔细阅读并完成相应的任务.
(1)、求证:DE是⊙O的切线.(2)、若DE=2,AF=3,直接写出AE的长.24. 阅读与思考:下面是小明同学的数学小论文,请仔细阅读并完成相应的任务.用函数观点认识一元二次方程根的情况
我们知道,一元二次方程ax2+bx+c=0(a≠0)的根就是相应的二次函数y=ax2+bx+c(a≠0)的图像(抛物线)与x轴交点的横坐标.抛物线与x轴的交点有三种情况:有两个交点、有一个交点、无交点与此相对应,一元二次方程的根也有三种情况:有两个不相等的实数根、有两个相等的实数根、无实数根.因此可用抛物线与x轴的交点个数确定一元二次方程根的情况.
下面根据抛物线的顶点坐标( , )和一元二次方程根的判别式△=b2-4ac,分a>0和a<0两种情况进行分析:
当a>0时,抛物线开口向上.①当△=b2-4ac>0时,有4ac-b2<0.
∵a>0,∴顶点纵坐标<0,
∴顶点在x轴的下方,抛物线与x轴有两个交点(如图①),

∴一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根.
②当△=b2-4ac=0时,有4ac-b2=0.
∵a>0,∴顶点纵坐标=0,
∴顶点在x轴上,抛物线与x轴有一个交点(如图②),

∴一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,
③当△=b2-4ac<0……
当a<0时,抛物线开口向下.……
任务:
(1)、上面小论文中的分析过程,主要运用的数学思想是(从下面选项中选出两个即可)A.数形结合
B.统计思想
C.分类讨论
D.转化思想
(2)、请参照小论文中当a>0时①②的分析过程,写出③中当a>0,△<0时,一元二次方程根的情况的分析过程,并画出相应的示意图.(3)、实际上,除一元二次方程外,初中数学还有一些知识也可以用函数观点来认识,例如:可用函数观点来认识一元一次方程的解,请你再举出一例.六、解答题(每小题10分,共20分)
-
25.
 (1)、如图①,△AOB和△COD是等腰直角三角形,∠AOB=∠COD=90°,点C在OA上,点D在线段BO的延长线上,连接AD、BC.线段AD与BC的数量关系为(2)、如图②,将图①中的△COD绕点O顺时针旋转a(0°<a<90°),第(1)问的结论是否仍然成立?如果成立,证明你的结论;若不成立,说明理由.(3)、如图③,若AB=5,点C是线段AB外一动点,AC=3,连接BC,将CB绕点C逆时针旋转90°得到CD,连接AD,解答下列问题.
(1)、如图①,△AOB和△COD是等腰直角三角形,∠AOB=∠COD=90°,点C在OA上,点D在线段BO的延长线上,连接AD、BC.线段AD与BC的数量关系为(2)、如图②,将图①中的△COD绕点O顺时针旋转a(0°<a<90°),第(1)问的结论是否仍然成立?如果成立,证明你的结论;若不成立,说明理由.(3)、如图③,若AB=5,点C是线段AB外一动点,AC=3,连接BC,将CB绕点C逆时针旋转90°得到CD,连接AD,解答下列问题.①当点C落在线段AD上时,AD的长为
②直接写出AD长度的最大值和最小值.
26. 已知抛物线y=-x2+bx+c(b,c为常数)经过点(0,-3)、(-6,-3).(1)、求此抛物线的解析式.(2)、此抛物线的顶点坐标为(3)、当-4≤x≤0时,求y的最大值和最小值.(4)、当m≤x≤0时,若y的最大值与最小值之和为2,直接写出m的值.