（北师大版）2022-2023学年九年级数学下册1.6 利用三角函数测高 同步测试
试卷更新日期：2022-11-14 类型：同步测试
一、单选题
-
1. 如图是大坝的横断面，斜坡AB的坡度 i1 =1：2，背水坡CD的坡度i2=1：1，若坡面CD的长度为 米，则斜坡AB的长度为（ ）
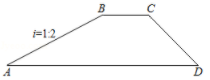A、 B、 C、 D、242. 如图，冬奥会滑雪场有一坡角为20°的滑雪道，滑雪道的长AC为100米，则BC的长为（ ）米．
A、 B、 C、 D、3. 已知一道斜坡的坡比为1： ，坡长为24米，那么坡高为（ ）米.A、 B、12 C、 D、64. 如图所示，河堤横断面迎水坡AB的坡比是 ，堤高 ，则坡面AB的长度是（ ）m
A、8 B、16 C、 D、5. 鹅岭公园是重庆最早的私家园林，前身为礼园，是国家级AAA旅游景区，园内有一瞰胜楼，登上高楼能欣赏到重庆的优美景色.周末，李明同学游览鹅岭公园，如图，在点A观察到瞰胜楼楼底点C的仰角为12°，楼顶点D的仰角为13°，测得斜坡BC的坡面距离BC 510米，斜坡BC的坡度 .则瞰胜楼的高度CD是（ ）米.（参考数据：tan12°≈0.2，tan13°≈0.23）
A、30 B、32 C、34 D、366. 如图是拦水坝的横断面，斜坡AB的水平宽度为12米，斜面坡度为1：2，则斜坡AB的长为（ ）米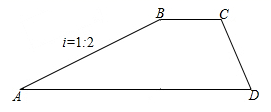
A、 B、 C、 D、247. 如图，滑雪场有一坡角为20°的滑道，滑雪道的长AC为100米，则BC的长为（ ）米．
A、 B、100cos20° C、 D、100sin20°8. 如图，小明家附近有一观光塔CD，他发现当光线角度发生变化时，观光塔的影子在地面上的长度也发生变化.经测量发现，当小明站在点A处时，塔顶D的仰角为37°，他继续往前再走5米到达点B（点A，B，C在同一直线上），此时塔顶D的仰角为53°，则观光塔CD的高度约为（ ）（精确到0.1米，参考数值： ， ）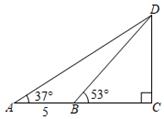
A、7.6米 B、7.8米 C、8.6米 D、8.8米9. 小明和好朋友一起去三亚旅游，他们租住的酒店AB坐落在坡度为i＝1：2.4的斜坡CD上，酒店AB高为129米．某天，小明在酒店顶楼的海景房A处向外看风景，发现酒店前有一座雕像C（雕像的高度忽略不计），已知雕像C距离海岸线上的点D的距离CD为260米，雕像C与酒店AB的水平距离为36米，他站在A处还看到远处海面上一艘即将靠岸的轮船E的俯角为27°．则轮船E距离海岸线上的点D的距离ED的长大约为（ ）米．（参考数据：tan27°≈0.5，sin27°≈0.45）
A、262 B、212 C、244 D、27610. 如图，已知点 、点 是同一幢楼上的两个不同位置，从 点观测标志物 的俯角是65°，从 点观测标志物 的俯角是35°，则 的度数为（ ）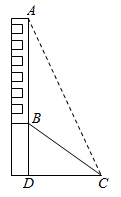
A、25° B、30° C、35° D、65°二、填空题
-
11. 如图，在小山的东侧A点有一个热气球，由于受西风的影响，以30米/分的速度沿与地面成75°角的方向飞行，25分钟后到达C处，此时热气球上的人测得小山西侧B点的俯角为30°，则小山东西两侧A、B两点间的距离为米.
12. 如图，已知斜坡AC的坡度i＝1：2，小明沿斜坡AC从点A行进10m至点B，在这个过程中小明升高 m.
13. 如图，在大楼AB的正前方有一斜坡CD，CD＝4米，坡角∠DCE＝30°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上.则大楼AB的高度 .（结果保留根号）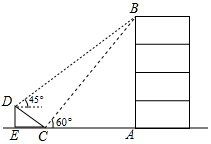
14. 某通信公司准备逐步在山上建设5G基站.如图，某处斜坡的坡角的正切值为 ， 通讯塔垂直于水平地面，在C处测得塔顶A的仰角为45°，在D处测得塔顶A的仰角为53°，斜坡路段长26米则通讯塔的高度约为米.（参考数据： ， ， ）
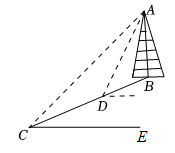15. 如图，河坝的横断面迎水坡AB的坡比是1：（坡比是坡面的铅直高度BC与水平宽度AC之比），坝高BC=6m，则坡面AB的长度是m.
三、解答题
-
16. 风力发电是指把风的动能转为电能．风能是一种清洁无公害的可再生能源，利用风力发电非常环保，且风能蕴量巨大，因此风力发电日益受到我们国家的重视．某校学生开展综合实践活动，测量风力发电扇叶轴心的高度．如图，已知测倾器的高度为1.6m，在测点A处安置测倾器，测得扇叶轴心点M的仰角 ， 再与点A相距3.5m的测点B处安置测倾器，测得点M的仰角（点A，B与N在一条直线上）求扇叶轴心离地面的高度的长．（精确到1m；参考数据： ， ， ）
17. 如图，小丽家住在巴河畔的电梯公寓AD内，她家的河对岸新建了一座大厦BC. 为了测量大厦的高度，小丽在她家的楼底A处测得大厦顶部B的仰角为45°，爬上楼顶D处得大厦顶部B的仰角为30°. 已知小丽家所住的电梯公寓高36米，请你帮助小丽计算出大厦高度BC，结果保留整数.（参考数据： ， ）
18. 如图，升国旗时，某同学站在离国旗20m的E处行注目礼（即BE=20m），当国旗升至旗杆顶端A时，该同学视线的仰角∠ADC=42°，已知他的双眼离地面的高度DE=1.60m．求旗杆AB的高度（结果精确到0.01m）．参考数据：sin42°≈0.6691，cos42°≈0.7431，tan42°≈0.9004．
四、综合题
-
19. 在一次课外活动中，某数学兴趣小组测量一棵树CD的高度.如图所示，测得斜坡BE的坡度i＝1：4（即AB：AE＝1：4），坡底AE的长为8米，在B处测得树CD顶部D的仰角为30°，在E处测得树CD顶部D的仰角为60°.
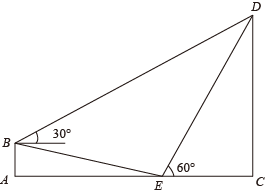(1)、求AB的高；(2)、求树高CD.（结果保留根号）20. 图（1）为某大型商场的自动扶梯．图（2）中的AB为从一楼到二楼的扶梯的侧面示意图．小明站在扶梯起点A处时，测得天花板上日光灯C的仰角为37°，此时他的眼睛D与地面的距离AD＝1.8m，之后他沿一楼扶梯到达顶端B后又沿BL（ ）向正前方走了2m，发现日光灯C刚好在他的正上方．已知自动扶梯AB的坡度为1：2.4，AB的长度是13m，（参考数据：sin37°≈0.6，cos37°＝0.8，tan37°≈0.75）．
(1)、求图中B到一楼地面的高度．(2)、求日光灯C到一楼地面的高度．（结果精确到十分位）．21. 如图，某建筑物BC上有一旗杆AB，小明在F处，由E点观察到旗杆顶部A的仰角为52°，底部B的仰角为45°，小明的观测点与地面距离EF为1.6m，
(1)、若F与BC相距12m，求建筑物BC的高度；(2)、若旗杆AB长3.15m，求建筑物BC的高度．（结果精确到0.1m）（参考数据： ≈1.414，sin52°≈0.788，tan52°≈1.280）．22. 如图大金鹰雕塑用线段MN表示，雄居在重庆南山鹞鹰岩上且垂直于地面，水泥浇铸，重千吨，外敷金箔，内设通道，游客可直登鹰的头部，上设有观景台，凭栏远眺，重庆数十里景物尽收眼底.如图，小明沿坡度的斜坡AN登山浏览大金鹰，小明在坡脚A测得大金鹰顶部M的仰角为45°，然后沿坡面AN行走52米到达B处，在B处测得大金鹰顶部M的仰角为60°（点A、B、M、N均在同一平面内）.（结果精确到1米，参考数据： ， ）
(1)、求B处的竖直高度；(2)、求大金鹰MN的高.23. 如图，建筑物后有一座小山， ， 测得小山坡脚C点与建筑物水平距离米，若山坡上E点处有一凉亭，且凉亭与坡脚距离米，某人从建筑物顶端A点测得E点处的俯角为.
(1)、求凉亭到地面的距离；(2)、求建筑物的高.（精确到）（参考数据： ， ， ， ， ， ， ）