（北师大版）2022-2023学年九年级数学下册1.3 三角函数的计算 同步测试

试卷更新日期：2022-11-14 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 四位学生用计算器求cos 27°40'的近似值的结果如下，正确的是（ ）
    A、0.885 7 B、0.885 6 C、0.885 2 D、0.885 1

    查看试题解析

  • 2. 用计算器比较tan 25°，sin 27°，cos 26°的大小关系是（ ）
    A、tan 25°<cos 26°<sin 27° B、tan 25°<sin 27°<cos 26° C、sin 27°<tan 25°<cos 26° D、cos 26°<tan 25°<sin 27°

    查看试题解析

  • 3. 用科学计算器求sin 9°的值，以下按键顺序正确的是（ ）
    A、sin9= B、9sin= C、sin9 D、9sin

    查看试题解析

  • 4. 在△ABC中，∠C=90°，BC=5，AB=13，用科学计算器求∠A约等于（ ）
    A、24°38' B、65°22' C、67°23' D、22°37'

    查看试题解析

  • 5. 为了方便行人推车过某天桥，市政府在10m高的天桥一侧修建了40m长的斜道（如图所示），我们可以借助科学计算器求这条斜道倾斜角的度数，具体按键顺序是（   ）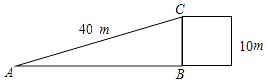

    A、 B、 C、 D、

    查看试题解析

  • 6. 下列说法正确的是（   ）
    A、求sin30°的按键顺序是 、30、= B、求23的按键顺序 、2、 、3、= C、求 8 的按键顺序是 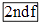、 、8、= D、已知sinA=0.5018，用计算器求锐角A的大小，按键顺序是 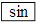、 、0.5018、=

    查看试题解析

  • 7. 如图，在△ABC中，∠ACB=90°，∠ABC=26°，BC=5．若用科学计算器求边AC的长，则下列按键顺序正确的是（   ）

    A、5÷tan26°= B、5÷sin26°= C、5×cos26°= D、5×tan26°=

    查看试题解析

  • 8. 已知sinα=12 ， 求α，若用计算器计算且结果为“30”，最后按键（　　）

    A、AC10N   B、SHIET   C、MODE D、SHIFT

    查看试题解析

  • 9. 已知sinA=0.1782，则锐角A的度数大约为（　　）

    A、8° B、9° C、10° D、12°

    查看试题解析

  • 10. 当锐角A的cosA＞22时，∠A的值为（　　）

    A、小于45° B、小于30° C、大于45° D、大于30°

    查看试题解析

二、填空题

  • 11. 用计算器计算:sin 51°30'+cos 49°50'-tan 46°10'的值约是.

    查看试题解析

  • 12. 如图，将一张矩形纸片ABCD沿CE折叠，B点恰好落在AD边上，设此点为F，展开后，若AB∶BC=4∶5，则∠CFD≈.(精确到0.01°)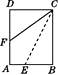

    查看试题解析

  • 13. 用科学记算器计算：2×sin15°×cos15°= 

    查看试题解析

  • 14. 利用计算器求sin20°tan35°的值时，按键顺序是​ 

    查看试题解析

  • 15. 已知α、β是锐角，且cotα＜cotβ，则α、β中较小的角是​ ．  

    查看试题解析

三、解答题

  • 16. 计算（结果保留小数点后四位）

    （1）sin23°5′+cos66°45′

    （2）sin27.8°﹣tan15°8′．

    查看试题解析

  • 17. 等腰三角形中，两腰和底的长分别是10和13，求三角形的三个内角的度数（精确到l′）．

    查看试题解析

  • 18.

    （1）用计算器计算并验证sin25°+sin46°与sin71°之间的大小关系：

    （2）若α、β、α+β都是锐角，猜想sinα+sinβ与sin（α+β）的大小关系：

    （3）请借助如图的图形证明上述猜想．

    查看试题解析

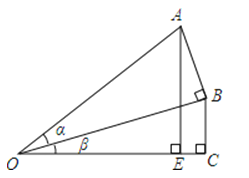
四、综合题

  • 19. 选做题（从下面两题中任选一题）
    (1)、用科学计算器计算：135× 13 sin13°≈（结果精确到0.1）
    (2)、已知α是锐角，且sin（α+15°）＝ 32 .计算 8 ﹣4cosα﹣（π﹣3.14）0+tanα+ (13)−1 的值

    查看试题解析

  • 20. 如图

    (1)、用计算器计算并验证 sin25°+sin46° 与 sin71° 之间的大小关系；
    (2)、若 α ， β ， α+β 都是锐角，猜想 sinα+sinβ 与 sin(α+β) 之间的大小关系；
    (3)、请借助如下图形证明上述猜想.

    查看试题解析

  • 21. 某“综合与实践”小组开展了测量本校旗杆高度的实践活动，他们制订了测量方案，并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差，小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如下表(不完整)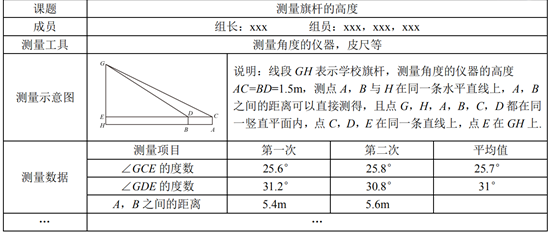

    (1)、任务一：两次测量A，B之间的距离的平均值是m.
    (2)、任务二：根据以上测量结果，请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.

    (参考数据：sin25.7°≈0.43，cos25.7°≈0.90，tan25.7°≈0.48，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60)

    (3)、任务三：该“综合与实践”小组在定制方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳.你认为其原因可能是什么？(写出一条即可).

    查看试题解析

  • 22. 如图，某数学兴趣小组为测量一颗古树BH和教学楼CG的高，先在A处用高1.5米的测角仪AF测得古树顶端H的仰角 ∠HFE 为 45° ，此时教学楼顶端G恰好在视线FH上，再向前走10米到达B处，又测得教学楼顶端G的仰角 ∠GED 为 60° ，点A、B、C三点在同一水平线上．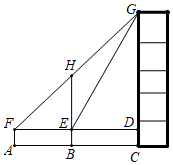

    (1)、求古树BH的高；
    (2)、求教学楼CG的高．（参考数据： 2=1.4 ， 3=1.7 ）

    查看试题解析

  • 23. 已知在梯形ABCD中，AD∥BC ， AC＝BC＝10，cos∠ACB＝ 45 ，点E在对角线AC上（不与点A、C重合），∠EDC＝∠ACB ， DE的延长线与射线CB交于点F ， 设AD的长为x ．

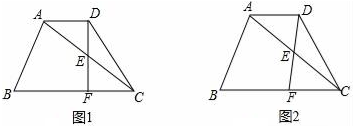    (1)、如图1，当DF⊥BC时，求AD的长；
    (2)、设EC＝y ， 求y关于x的函数解析式，并直接写出定义域；
    (3)、当△DFC是等腰三角形时，求AD的长．

    查看试题解析