2022年秋季浙教版数学九年级上册期末复习检测B
试卷更新日期:2022-11-11 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 在某市组织的物理实验操作考试中,考试所用实验室共有24个测试位,分成6组,同组4个测试位各有一道相同试题,各组的试题不同,分别标记为A,B,C,D,E,F,考生从中随机抽取一道试题,则某个考生抽到试题A的概率为( )A、 B、 C、 D、2. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或43. 如图, 内接于 ,CD是 的直径, ,则 ( )
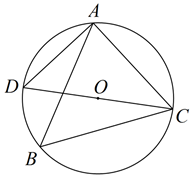 A、70° B、60° C、50° D、40°4. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )
A、70° B、60° C、50° D、40°4. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )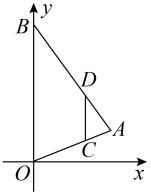 A、4 B、5 C、6 D、75. 如图,在 △ABC中,D、E分别为线段BC、BA的中点,设△ABC的面积为S1 , △EBD的面积为S2 . 则 =( )
A、4 B、5 C、6 D、75. 如图,在 △ABC中,D、E分别为线段BC、BA的中点,设△ABC的面积为S1 , △EBD的面积为S2 . 则 =( ) A、 B、 C、 D、6. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A、 B、 C、 D、6. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( ) A、
A、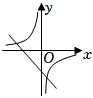 B、
B、 C、
C、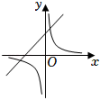 D、
D、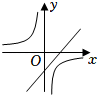 7. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
7. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、8. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A、 B、 C、 D、8. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )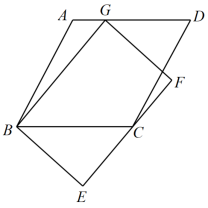 A、 B、 C、 D、39. 如图,在正方形中,和交于点O,过点O的直线交于点(E不与A,B重合),交于点F.以点O为圆心,为半径的圆交直线于点M,N.若 , 则图中阴影部分的面积为( )
A、 B、 C、 D、39. 如图,在正方形中,和交于点O,过点O的直线交于点(E不与A,B重合),交于点F.以点O为圆心,为半径的圆交直线于点M,N.若 , 则图中阴影部分的面积为( )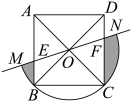 EA、 B、 C、 D、10. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .
EA、 B、 C、 D、10. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .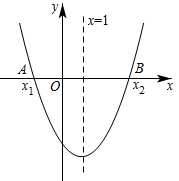
正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共18分)
-
11. 如图,在矩形中,若 , 则的长为 .
 12. 把二次函数y=x2+4x+m的图象向上平移1个单位长度,再向右平移3个单位长度,如果平移后所得抛物线与坐标轴有且只有一个公共点,那么m应满足条件:.13. 如图,在中, , 以为直径的交边于D,E两点, , 则的长是 .
12. 把二次函数y=x2+4x+m的图象向上平移1个单位长度,再向右平移3个单位长度,如果平移后所得抛物线与坐标轴有且只有一个公共点,那么m应满足条件:.13. 如图,在中, , 以为直径的交边于D,E两点, , 则的长是 .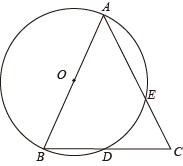 14. 如图,是一名男生推铅球时,铅球行进过程中形成的抛物线.按照图中所示的平面直角坐标系,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 , 则铅球推出的水平距离OA的长是m.
14. 如图,是一名男生推铅球时,铅球行进过程中形成的抛物线.按照图中所示的平面直角坐标系,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 , 则铅球推出的水平距离OA的长是m. 15. 如图,在矩形 ABCD中, AB=1,BC=2,以B为圆心,BC 的长为半轻画弧,交 AD 于点 E.则图中阴影部分的面积为 . (结果保留 π)
15. 如图,在矩形 ABCD中, AB=1,BC=2,以B为圆心,BC 的长为半轻画弧,交 AD 于点 E.则图中阴影部分的面积为 . (结果保留 π)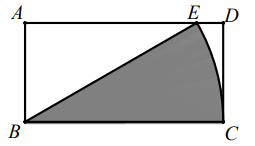 16. 如图,已知菱形的边长为2, , E为的中点,F为的中点,与相交于点G,则的长等于 .
16. 如图,已知菱形的边长为2, , E为的中点,F为的中点,与相交于点G,则的长等于 .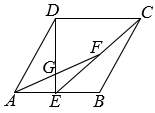
三、解答题(共8题,共72分)
-
17. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD.
 (1)、求证: .(2)、若 , , 求阴影部分的面积.18. 今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.
(1)、求证: .(2)、若 , , 求阴影部分的面积.18. 今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.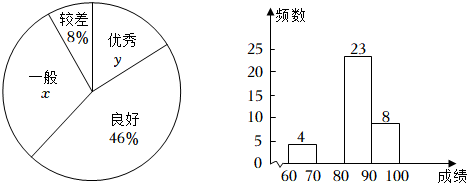
请根据统计图提供的信息,回答如下问题:
(1)、x= ▲ , y= ▲ , 并将直方图补充完整;(2)、已知90≤a≤100这组的具体成绩为93,94,99,91,100,94,96,98,则这8个数据的中位数是 , 众数是;(3)、若该校共有1200人,估计该校学生对团史掌握程度达到优秀的人数;(4)、本次知识竞赛超过95分的学生中有3名女生,1名男生,现从以上4人中随机抽取2人去参加全市的团史知识竞赛,请用列表或画树状图的方法,求恰好抽中2名女生参加知识竞赛的概率.19. 如图,在⊙O中,直径AB与弦CD相交于点E,连接AC、BD.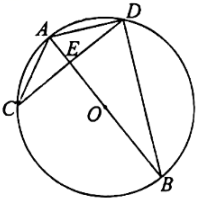 (1)、求证:△AEC∽△DEB;(2)、连接AD,若AD=3,∠C=30°,求⊙O的半径.20. 某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现.,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)、求证:△AEC∽△DEB;(2)、连接AD,若AD=3,∠C=30°,求⊙O的半径.20. 某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现.,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.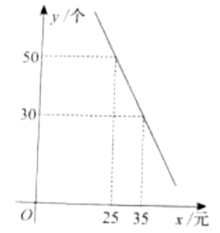 (1)、求y与x的函数关系式(不要求写出自变量x的取值范围);(2)、若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?(3)、设该玩具日销售利润为w元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?21. 如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)、求y与x的函数关系式(不要求写出自变量x的取值范围);(2)、若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?(3)、设该玩具日销售利润为w元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?21. 如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).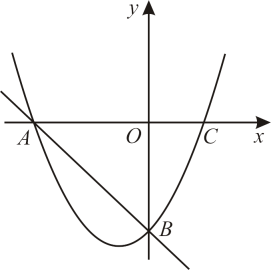 (1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.22. 四边形内接于 , 直径与弦交于点 , 直线与相切于点 .
(1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.22. 四边形内接于 , 直径与弦交于点 , 直线与相切于点 .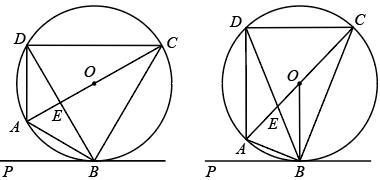 (1)、如图1,若 , 且 , 求证:平分;(2)、如图2,连接 , 若 , 求证: .23. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.
(1)、如图1,若 , 且 , 求证:平分;(2)、如图2,连接 , 若 , 求证: .23. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线 , 与的面积相等吗?为什么?
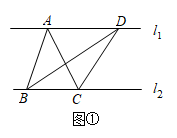
解:相等.理由如下:
设与之间的距离为 , 则 , .
∴ .
【探究】
(1)、如图②,当点在 , 之间时,设点 , 到直线的距离分别为 , , 则 .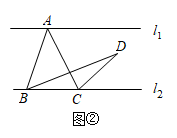
证明:∵ ▲
▲
▲
(2)、如图③,当点在 , 之间时,连接并延长交于点 , 则 .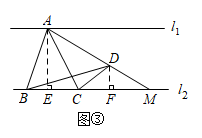
证明:过点作 , 垂足为 , 过点作 , 垂足为 , 则 ,
∴ ▲ .
∴ ▲ .
∴ .
由【探究】(1)可知 ▲ ,
∴ .
(3)、如图④,当点在下方时,连接交于点 . 若点 , , 所对应的刻度值分别为5,1.5,0,的值为 .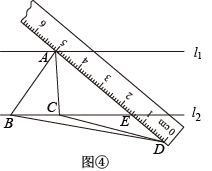 24. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,顶点为 , 抛物线的对称轴交直线于点E.
24. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,顶点为 , 抛物线的对称轴交直线于点E. (1)、求抛物线的表达式;(2)、把上述抛物线沿它的对称轴向下平移,平移的距离为 , 在平移过程中,该抛物线与直线始终有交点,求h的最大值;(3)、M是(1)中抛物线上一点,N是直线上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、把上述抛物线沿它的对称轴向下平移,平移的距离为 , 在平移过程中,该抛物线与直线始终有交点,求h的最大值;(3)、M是(1)中抛物线上一点,N是直线上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.