浙江省宁波市鄞州区七校联考2022-2023学年八年级上学期期中检测数学试题
试卷更新日期:2022-11-11 类型:期中考试
一、选择题
-
1. 下列图形中,轴对称图形有( )
 A、1个 B、2个 C、3个 D、4个2. 若a<b,b<2a,则a与2a的大小关系是( )A、a<2a B、a>2a C、a=2a D、与a的取值有关3. 已知三角形的两边长分别为3和4,则第三边长的取值范围在数轴上表示正确的是( )A、
A、1个 B、2个 C、3个 D、4个2. 若a<b,b<2a,则a与2a的大小关系是( )A、a<2a B、a>2a C、a=2a D、与a的取值有关3. 已知三角形的两边长分别为3和4,则第三边长的取值范围在数轴上表示正确的是( )A、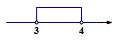 B、
B、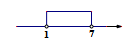 C、
C、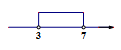 D、
D、 4. 下列命题中,是真命题的是( )A、成轴对称的两个图形是全等图形 B、面积相等的两个三角形全等 C、三角形的三条高线相交于三角形内一点 D、内错角相等5. 不等式3+x>3x-5的正整数解有( )A、1个 B、2个 C、3个 D、4个6. 如图,CD⊥AB于点D,已知∠ABC是钝角,则( )
4. 下列命题中,是真命题的是( )A、成轴对称的两个图形是全等图形 B、面积相等的两个三角形全等 C、三角形的三条高线相交于三角形内一点 D、内错角相等5. 不等式3+x>3x-5的正整数解有( )A、1个 B、2个 C、3个 D、4个6. 如图,CD⊥AB于点D,已知∠ABC是钝角,则( )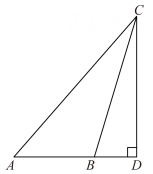 A、线段CD是△ABC的AC边上的高线 B、线段CD是△ABC的AB边上的高线 C、线段AD是△ABC的BC边上的高线 D、线段AD是△ABC的AC边上的高线7. 已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
A、线段CD是△ABC的AC边上的高线 B、线段CD是△ABC的AB边上的高线 C、线段AD是△ABC的BC边上的高线 D、线段AD是△ABC的AC边上的高线7. 已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( ) A、∠A与∠D互为余角 B、∠A=∠2 C、△ABC≌△CED D、∠1=∠28. 如图,在△ABC中,BD=CD, AD⊥BC,垂足为D,E是AC的中点.若AB=5,则DE的长为( )
A、∠A与∠D互为余角 B、∠A=∠2 C、△ABC≌△CED D、∠1=∠28. 如图,在△ABC中,BD=CD, AD⊥BC,垂足为D,E是AC的中点.若AB=5,则DE的长为( )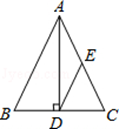 A、2 B、2.5 C、3 D、49. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2 , 则S阴影等于( ).
A、2 B、2.5 C、3 D、49. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2 , 则S阴影等于( ). A、2 B、3 C、4 D、510. 如图,在等边△ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相较于O,若OB=2则B点到AQ的距离等于( )
A、2 B、3 C、4 D、510. 如图,在等边△ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相较于O,若OB=2则B点到AQ的距离等于( ) A、1 B、2 C、 D、
A、1 B、2 C、 D、二、细心填一填:(每小题3分,共24分)
-
11. 如图,∠ACD是△ABC的外角,若∠ACD=125°,∠A=75°,则∠B=度.
 12. 已知△ABC是等腰三角形.若∠A=80°,则△ABC的顶角度数是13. 命题“等腰三角形的两个底角相等.”的逆命题是 .14. 如图,在△ABC中,AB=AC,AD⊥BC于点D,若AB=6,CD=4,则△ABC的周长是 .
12. 已知△ABC是等腰三角形.若∠A=80°,则△ABC的顶角度数是13. 命题“等腰三角形的两个底角相等.”的逆命题是 .14. 如图,在△ABC中,AB=AC,AD⊥BC于点D,若AB=6,CD=4,则△ABC的周长是 . 15. 如图,△ABC中∠ABC=∠ACB,AB的垂直平分线交AC于点D.若∠A=40°,则∠DBC=
15. 如图,△ABC中∠ABC=∠ACB,AB的垂直平分线交AC于点D.若∠A=40°,则∠DBC=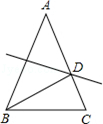 16. 下列条件:①∠C=∠A-∠B;②∠A:∠B:∠C=5∶2∶3;③a=c,b=c;④a∶b∶c=1∶2: , 则能确定△ABC是直角三角形的条件有个.17. 不等式组
16. 下列条件:①∠C=∠A-∠B;②∠A:∠B:∠C=5∶2∶3;③a=c,b=c;④a∶b∶c=1∶2: , 则能确定△ABC是直角三角形的条件有个.17. 不等式组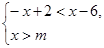 的解集是
的解集是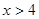 , 那么
, 那么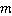 的取值范围是 18. 如图:在△ABC中,∠C=90°,BC=6cm,AC=8cm,BD是∠ABC的角平分线。
的取值范围是 18. 如图:在△ABC中,∠C=90°,BC=6cm,AC=8cm,BD是∠ABC的角平分线。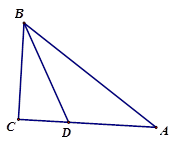 (1)、则CD=;(2)、若点E是线段AB上的一个动点,从点B以每秒1cm的速度向A运动, 秒种后△EAD是直角三角形
(1)、则CD=;(2)、若点E是线段AB上的一个动点,从点B以每秒1cm的速度向A运动, 秒种后△EAD是直角三角形三、用心做一做(共46分)
-
19. 解下列不等式(组),并把(1)的解集在数轴上表示出来(1)、7x ≥5x+2(2)、解不等式组:20. 在如图所示的6×6的网格中,每个小正方形的边长均为1个单位.
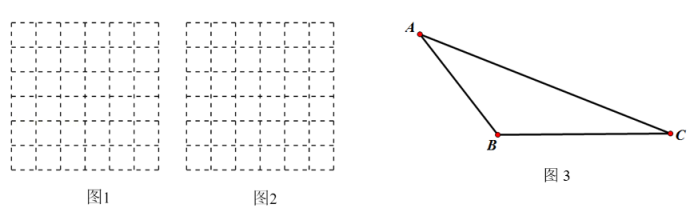 (1)、请你在图1中画一个以格点为顶点,面积为6个平方单位的等腰三角形:(2)、请你在图2中画一个以格点为顶点,一条直角边边长为的直角三角形.(3)、请你在图3中画出△ABC的边BC上的高AD,∠ACB的角平线CE21. 如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=140°,求∠D的度数.
(1)、请你在图1中画一个以格点为顶点,面积为6个平方单位的等腰三角形:(2)、请你在图2中画一个以格点为顶点,一条直角边边长为的直角三角形.(3)、请你在图3中画出△ABC的边BC上的高AD,∠ACB的角平线CE21. 如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=140°,求∠D的度数. 22. 双十一前,妈妈购买了甲种物品15个,乙种物品20个,共花费250元,已知购买一个甲种物品比购买一个乙种物品多花费5元.(1)、求双十一前购买一个甲种、一个乙种物品各需多少元?(2)、双十一期间,甲种物品售价比上一次购买时减价2元,乙种物品按上一次购买时售价的8折出售.如果妈妈此时再次购买甲、乙两种物品共35个,总费用不超过225元,求至多需要购买多少个甲种物品?23. 如图
22. 双十一前,妈妈购买了甲种物品15个,乙种物品20个,共花费250元,已知购买一个甲种物品比购买一个乙种物品多花费5元.(1)、求双十一前购买一个甲种、一个乙种物品各需多少元?(2)、双十一期间,甲种物品售价比上一次购买时减价2元,乙种物品按上一次购买时售价的8折出售.如果妈妈此时再次购买甲、乙两种物品共35个,总费用不超过225元,求至多需要购买多少个甲种物品?23. 如图
 (1)、如图1,△ABC中,作∠ABC、∠ACB的角平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.
(1)、如图1,△ABC中,作∠ABC、∠ACB的角平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.求证:OE=BE;
(2)、若△ABC 的周长是25,BC=9,试求出△AEF的周长;(3)、如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.则EF,BE,CF之间有何数量关系.直接写出结论。24. 如图1,△ABC和△DEC均为等腰直角三角形, , 点B,D在同一直线上,连接AD,BD. (1)、求证:△ACD≌△BCE;(2)、探求AD与BE的数量和位置关系(3)、若AC= , EC= 求线段AD的长.
(1)、求证:△ACD≌△BCE;(2)、探求AD与BE的数量和位置关系(3)、若AC= , EC= 求线段AD的长.