浙江省温州市洞头区2022-2023学年九年级上学期期中检测数学试题
试卷更新日期:2022-11-11 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分.)
-
1.
将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 已知a=3b,则a:b的值是( )A、1:2 B、1:3 C、2:1 D、3:13. 对于二次函数的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线 C、顶点坐标是(1,3) D、过点(0,3)4. 如图,在△ABC中,点D、E分别在线段AB、AC上,DE∥BC,AD:AB=1:3,若△ADE的面积是1,则△ABC的面积是( )
2. 已知a=3b,则a:b的值是( )A、1:2 B、1:3 C、2:1 D、3:13. 对于二次函数的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线 C、顶点坐标是(1,3) D、过点(0,3)4. 如图,在△ABC中,点D、E分别在线段AB、AC上,DE∥BC,AD:AB=1:3,若△ADE的面积是1,则△ABC的面积是( ) A、3 B、4 C、8 D、95. 如图A是某公园的进口,B,C,D是三个不同的出口,小明从A处进入公园,那么从B,C,D三个出口中恰好在C出口出来的概率为( )
A、3 B、4 C、8 D、95. 如图A是某公园的进口,B,C,D是三个不同的出口,小明从A处进入公园,那么从B,C,D三个出口中恰好在C出口出来的概率为( )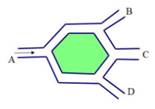 A、 B、 C、 D、6. 已知(-4,y1),(-2,y2),(1,y3)是抛物线y=-x2-2x上的点,则( )A、y3<y1<y2 B、y3<y2<y1 C、y2<y3<y1 D、y1<y3<y27. 下表是部分二次函数的自变量与函数值的对应值:
A、 B、 C、 D、6. 已知(-4,y1),(-2,y2),(1,y3)是抛物线y=-x2-2x上的点,则( )A、y3<y1<y2 B、y3<y2<y1 C、y2<y3<y1 D、y1<y3<y27. 下表是部分二次函数的自变量与函数值的对应值:1
1.1
1.2
1.3
1.4
-1
-0.49
0.04
0.59
1.16
那么方程的一个根在( )范围之间。
A、4~1.1 B、1.1~1.2 C、1.2~1.3 D、1.3~1.48. 如图,点P是△ABC的重心,过点P作DE∥AC交BC,AB于D,E,EF∥BC交AC于点F,若BC=11,则EF的长为( ) A、 B、3 C、 D、49. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
A、 B、3 C、 D、49. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:① 当x>-1时,y的值随x值的增大而增大;② a-b+c>0;③ 4a+b=0;④ 9a+c>3b;
其中正确的结论是( ) A、① B、② C、③ D、④10. 在一次实验操作中,如图①是一个长和宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6;现将图①容器向右倾倒,按图放置,发现此时水面恰好触到容器口边缘,则图②中水面高度为( )
A、① B、② C、③ D、④10. 在一次实验操作中,如图①是一个长和宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6;现将图①容器向右倾倒,按图放置,发现此时水面恰好触到容器口边缘,则图②中水面高度为( )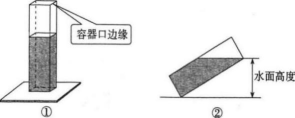 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有8小题,每小题3分,共24分)
-
11. 将抛物线y=x2向上平移2个单位后得到新的抛物线的表达式为 .12. 在中, , , AB=4; 如果以点A为圆心,AC为半径作⊙A,那么斜边AB的中点D在⊙A . (填“内”、“上”或者“外”)13. 从一个不透明的口袋中随机摸出1个球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中有个白球.14. 如图,若AC是BC与AB的比例中项,AB=4,求AC=.
 15. 已知二次函数(c为常数)的图象位于轴上方,则c可能取的整数为 . (写出一个即可)16. 已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分的面积是 .
15. 已知二次函数(c为常数)的图象位于轴上方,则c可能取的整数为 . (写出一个即可)16. 已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分的面积是 . 17. 已知当时,二次函数的函数值y大于0,则的取值范围为 .18. 如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,是杠杆,弹袋挂在点 , 重锤挂在点 , 点为支点,点是水平底板上的一点,米,米.
17. 已知当时,二次函数的函数值y大于0,则的取值范围为 .18. 如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,是杠杆,弹袋挂在点 , 重锤挂在点 , 点为支点,点是水平底板上的一点,米,米.
 (1)、投石车准备时,点恰好与点重合,此时和垂直,则米.(2)、投石车投石过程中,的延长线交线段于点 , 若:: , 则点距地面为米.
(1)、投石车准备时,点恰好与点重合,此时和垂直,则米.(2)、投石车投石过程中,的延长线交线段于点 , 若:: , 则点距地面为米.三、解答题(本题有6小题,共46分.)
-
19. 利用网格和无刻度的直尺作图,保留痕迹.如图,在边长为1个单位长度的小正方形组成的6×6网格中,点A、B、C、D均在格点上.
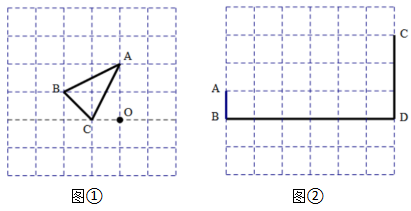 (1)、在图①中,以点O为位似中心,画△DEF,使△ABC与△DEF位似,且位似比为1:2(2)、在图②中的BD上找一点P,使△APB△CPD20. 小明,小亮都想去观看电影,但是只有一张电影票,他们决定采取抽卡片的办法确定谁去,规定如下:将正面分别标有数字1,2,3的三张卡片除数字外其余都同洗匀后背面朝上放置在桌面上,随机抽出一张记下数字后放回 , 重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字,如果两个数字的积为奇数,则小明去;如果两个数字的积为偶数,则小亮去.(1)、请用列表或树状图的方法表示抽出的两张卡片上的数字积的所有可能出现的结果;(2)、你认为这个规则公平吗?请说明理由.21. 如图,在矩形ABCD中,AB=2,BC=4,E,F,G,H分别是AB,BC,CD,DA上一点(不与各顶点重合),且AE=AH=CG=CF,记四边形EFGH面积为S(图中阴影),AE=x.
(1)、在图①中,以点O为位似中心,画△DEF,使△ABC与△DEF位似,且位似比为1:2(2)、在图②中的BD上找一点P,使△APB△CPD20. 小明,小亮都想去观看电影,但是只有一张电影票,他们决定采取抽卡片的办法确定谁去,规定如下:将正面分别标有数字1,2,3的三张卡片除数字外其余都同洗匀后背面朝上放置在桌面上,随机抽出一张记下数字后放回 , 重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字,如果两个数字的积为奇数,则小明去;如果两个数字的积为偶数,则小亮去.(1)、请用列表或树状图的方法表示抽出的两张卡片上的数字积的所有可能出现的结果;(2)、你认为这个规则公平吗?请说明理由.21. 如图,在矩形ABCD中,AB=2,BC=4,E,F,G,H分别是AB,BC,CD,DA上一点(不与各顶点重合),且AE=AH=CG=CF,记四边形EFGH面积为S(图中阴影),AE=x. (1)、求S关于x的函数表达式,并直接写出自变量x的取值范围.(2)、当x为何值时,S的值最大,并写出S的最大值.22. 如图,在矩形ABCD中,AB= , 点E是BC的中点,AE⊥BD于点F.
(1)、求S关于x的函数表达式,并直接写出自变量x的取值范围.(2)、当x为何值时,S的值最大,并写出S的最大值.22. 如图,在矩形ABCD中,AB= , 点E是BC的中点,AE⊥BD于点F. (1)、求BE的长;(2)、延长FE交DC的延长线于点G,求证:23.
(1)、求BE的长;(2)、延长FE交DC的延长线于点G,求证:23.如何确定隧道中警示灯带的安装方案?
素材1
2022年10月,温州市府东路过江通道工程正式开工,建成后将成为温州瓯江第一条超大直径江底行车隧道。隧道顶部横截面可视为抛物线,如图1,隧道底部宽AB为10m,高OC为5m.


素材2
货车司机长时间在隧道内行车容易疲劳驾驶,为了安全,拟在隧道顶部安装上下长度为20cm的警示灯带,沿抛物线安装。(如图2).为了实效,相邻两条灯带的水平间距均为0.8m(灯带宽度可忽略);普通货车的高度大约为2.5m(载货后高度),货车顶部与警示灯带底部的距离应不少于50cm。灯带安装好后成轴对称分布.
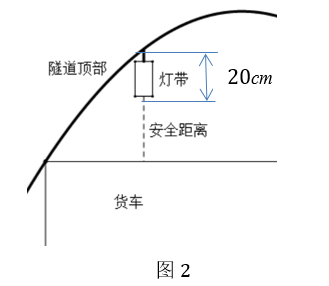
问题解决
任务1
确定隧道形状
在图1中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究安装范围
在你建立的坐标系中,在安全的前提下,确定灯带安装点的横、纵坐标的取值范围.
任务3
拟定设计方案
求出同一个横截面下,最多能安装几条灯带,并根据你所建立的坐标系,求出最右边一条灯带安装点的横坐标.
24. 如图,在矩形ABCD中,E为AD边中点,在BC延长线上任取一点N,过N作BE的中垂线,分别交AB,BE,CD于点F,H,G,延长FE交CD的延长线于点M. (1)、证明:△ABE∽△CNG.(2)、连接BG,当AB=CN时,求∠EBG的度数.(3)、当BC=CN时,的值为 . (直接写出答案)
(1)、证明:△ABE∽△CNG.(2)、连接BG,当AB=CN时,求∠EBG的度数.(3)、当BC=CN时,的值为 . (直接写出答案)