浙江省温州市洞头区2022-2023学年八年级上学期期中检测数学试题

试卷更新日期：2022-11-11 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分.）

1. 下列美丽的图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段能首尾相接构成三角形的是（）

A、1， 2， 3 B、4， 4， 7 C、20， 15， 3 D、6， 9， 2

查看试题解析
3. 如图，在数轴上表示的是下列哪个不等式（）

A、 $x > - 2$ B、 $x < - 2$ C、 $x \geq - 2$ D、 $x \leq - 2$

查看试题解析
4. 如图，AC是△ABC和△ADC的公共边，下列补充条件中，不能判定△ABC≌△ADC的是（）

A、AB=AD， ∠1=∠2 B、AD=AB， ∠3=∠4 C、∠1=∠2，∠3=∠4 D、∠1=∠2， ∠B=∠D

查看试题解析
5. 如图，在△ABC中，∠BAC=90°，AB=8，AC=6，点D为 BC 的中点，则AD 的长为（）

A、4.8 B、5 C、6 D、8

查看试题解析
6. 若等腰三角形有一个角是40°，则它的底角为（）

A、40° B、70° C、40°或70 D、40°或100°

查看试题解析
7. 若 $m > n$ ，则下列不等式中正确的是（）

A、 $m + 2 < n + 2$ B、 $- \frac{1}{2} m > - \frac{1}{2} n$ C、 $n - m > 0$ D、 $- 2 m + 1 < - 2 n + 1$

查看试题解析
8. 如图，在△ABC中，AD是角平分线，AE是高，已知∠B=50°，∠C=60°，那么∠EAD的度数为（）

A、5° B、15° C、25° D、35°

查看试题解析
9. 已知关于 $x$ 的不等式x－a≤0的正整数解恰好为1，2，3，则 $a$ 的取值范围是（）

A、a≥3 B、3≤a＜4 C、3＜a≤4 D、3≤a≤4

查看试题解析
10. 如图1，四个全等的直角三角形围成一个大正方形，中间是个小正方形，这个图形是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”.在弦图中（如图2）连结AF，DE，并延长DE交AF于点K，连结KG. 若AH=2DH = $2 \sqrt{2}$ ，则KG的长为（）

A、2 B、 $\frac{3}{2} \sqrt{2}$ C、 $\sqrt{5}$ D、 $2 \sqrt{2}$

查看试题解析

二、填空题（本题有8小题，每小题3分，共24分）

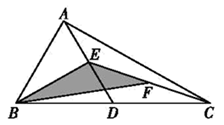
11. “x的2倍与1的和大于3"用不等式表示为．

查看试题解析
12. 证明“若 $| a | > 1$ ，则 $a > 1$ ”是假命题的反例可以是a =.（写一个即可）

查看试题解析
13. 写出“在同一个三角形中，等边对等角”的逆命题是．

查看试题解析
14. 如图，△ABC中，∠ABC和∠ACB的平分线交于点P，若∠A=70⁰ ，则∠BPC=；

查看试题解析
15. 若关于x的方程x－m=4的解满足不等式2x+1 >3，则 $m$ 可取的负整数为= ．

查看试题解析
16. 如图，在 $Δ A B C$ 中，已知 $D$ ， $E$ ， $F$ 分别为 $B C$ ， $A D$ ， $C E$ 的中点，且 $S_{Δ A B C} = 8 c m^{2}$ ，则图中阴影部分 $Δ B E F$ 的面积等于 $c m^{2}$ .

查看试题解析
17. 如图，△ABC中，AB=AC，AD为BC上的高线，E为AB边上一点，EF⊥BC于点F，交CA的延长线于点G. 已知EF=2，EG=3. 则AD的长为．

查看试题解析
18. 如图1是一种可折叠手机平板支架，由托板、支撑板和底座组成，手机放置在托板上，
图2是其侧面结构示意图.量得托板长AB＝17cm，支撑板长CD=12㎝，底座长DE=13㎝，

托板AB固定在支撑板的端点C处，托板AB可绕点C转动，支撑板CD可绕点D转动，当∠ACD＝2∠D＝60°时，点A到点D的距离恰好是点C到直线DE的距离的2倍，则BC=㎝．为了观看舒适，把AB绕点C旋转，再将CD绕点D旋转，使点B与点E重合，则此时点A到直线DE的距离为cm.

查看试题解析

三、解答题（本题有6小题，共46分.）

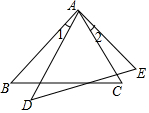
19. 解不等式组： ${\begin{matrix} \frac{x - 3}{2} + 3 \geq x \\ 1 - 3 (x - 1) < 7 \end{matrix}$ ，并把解集表示在数轴上．

查看试题解析
20. 如图，在△ABC和△ADE中，AB=AD，∠B=∠D，∠1=∠2．
求证：BC=DE．

查看试题解析
21. 图1，图2是“5×7”方格纸，方格纸中的每个小正方形的边长均为1，点A，B，C，D是方格纸上的四个格点（小正方形的顶点称为格点）．

(1)、在图1中画一个等腰三角形ADE，其中点E在格点上，且不在线段AB或CD上；

(2)、在图2中画线段AM与BN，使AM=BN，其中点M，N分别是BC，CD上的格点（不与端点重合）．

查看试题解析
22. 如图：在△ABC中，∠ACB＝90°，AC＝BC，AE是BC边上的中线，
过点C作CF⊥AE，垂足为F，过点B作BC的垂线交CF的延长线于点D．

(1)、求证：AE＝CD．

(2)、若BD＝1，求AE．

查看试题解析

23. 根据以下素材，探索完成任务

如何运输最省?
素材一	为做到“动态清零”，市卫生防疫部门需运输一批疫苗到某县，现有冷链车A 和 B型两种运输车，其中 $A$ 型冷链运输车一次可运输200盒疫苗， $B$ 型冷链运输车一次可运输150盒疫苗.
素材二	$A$ 型冷链运输车一次需费用5000元， $B$ 型冷链运输车一次需费用3000元.
问题解决
任务1	若某县需要1500盒疫苗，市卫生防疫部门只安排 $A$ 型冷链运输车，则至少需 $A$ 型冷链运输车多少辆？
任务2	市卫生防疫部门用上述两种冷冻车共12辆运输这批疫苗 $.$ 若运输疫苗不少于2100盒，且总费用小于54000元请你列出所有的运输方案.
任务3	在任务2的条件下，由于A型和 B型两种运输车，运输时走不同高速路线，A型需a元过路费， B型（100-a）元过路费，求如何安排两种车型运输的过路费总和最少？

查看试题解析

24. 如图，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，AD=2，E为AC边上的动点（不与A，C重合），连结BE，作AG⊥BE，垂足为F，交BC于点G，连结EG.
（备用图）

(1)、求AB=（直接写出答案）

(2)、若∠AEB=∠AGB时，
①求证：AB=BG.

②求△EGC的周长.

(3)、当∠AEB=∠GEC时，AE的长为（直接写出答案）

查看试题解析