浙江省金华市永康三中2022-2023学年九年级上学期第一次独立作业数学试卷

试卷更新日期：2022-11-11 类型：月考试卷

进入出卷网下载

一、单选题（本题有10小题，每小题3分，共30分）

1. 下列事件中，是必然事件的是（）

A、抛掷一个骰子，出现8点朝上 B、三角形的内角和是 $180 °$ C、汽车经过一个有红绿灯的路口时，前方恰好是绿灯 D、明天考试，小明会考满分

查看试题解析
2. 某人在做抛掷硬币试验中，抛掷n次，正面朝上有m次，若正面朝上的频率是P＝ $\frac{m}{n}$ ，则下列说法正确的是（）

A、P一定等于0.5 B、多投一次，P更接近0.5 C、P一定不等于0.5 D、投掷次数逐渐增加，P稳定在0.5附近

查看试题解析
3. 在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球，如果口袋中装有4个黑球且摸到黑球的概率为 $\frac{1}{3}$ ，那么口袋中球的总数为（　　）

A、12个 B、9个 C、6个 D、3个

查看试题解析
4. 在四张完全相同的卡片上，分别画有圆，等腰三角形，直角三角形，菱形，现从中随机抽取一张，卡片上的图形恰好是中心对称图形的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
5. 如图，在⊙O中，∠BOC＝130°，点A在 $\overset{⌢}{B A C}$ 上，则∠BAC的度数为（）

A、55° B、65° C、75° D、130°

查看试题解析
6. 一个点到圆的最小距离为3cm，最大距离为6cm，则该圆的直径是（）

A、1.5cm B、1.5cm或4.5cm C、4.5cm D、3cm或9cm

查看试题解析
7. 如图，⊙O中，半径OC＝2，弦AB垂直平分OC，则AB的长是（）

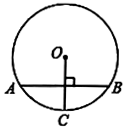A、3 B、4 C、2 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
8. 如图，△ABC内接于⊙O，AD是⊙O的直径，若∠B＝20°，则∠CAD的度数是（）

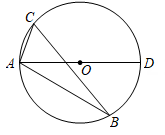A、60° B、65° C、70° D、75°

查看试题解析
9. 如图，四边形ABCD内接于⊙O，D是 $\overset{⌢}{A C}$ 的中点，若∠B＝70°，则∠CAD的度数为（）

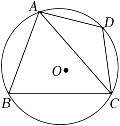A、70° B、55° C、35° D、20°

查看试题解析
10. 如图，四边形ABCD为矩形，AB＝3，BC＝4，点P是线段BC上一动点，点M为线段AP上一点，∠ADM＝∠BAP，则BM的最小值为（）

A、 $\frac{5}{2}$ B、 $\frac{12}{5}$ C、 $\sqrt{13}$ - $\frac{3}{2}$ D、 $\sqrt{13}$ -2

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 一个不透明的袋子里装有5个红球和6个白球，它们除颜色外其余都相同．从袋中任意摸出一个球是红球的概率为

查看试题解析
12. 从 $\sqrt{2}$ ， -1，π，0，3这五个数中随机抽取一个数，恰好是无理数的概率是．

查看试题解析
13. 如图，四边形ABCD内接于⊙O，∠A＝125°，则∠C的度数为．

查看试题解析
14. 某辆有轨电车共有3节车厢，设乘客乘坐任意一节车厢的机会均等，若甲、乙两位乘客同时乘坐同一列有轨电车，则甲和乙乘坐同一节车厢的概率是.

查看试题解析
15. 若圆中的一条弦和半径相等，则这条弦所对的圆周角为．

查看试题解析
16. 如图，桥拱 $\overset{⌢}{A C B}$ 关于水面AB反射的影子 $\overset{⌢}{A O B}$ 经过 $\overset{⌢}{A C B}$ 所在的圆心O，已知水面宽AB＝6米，则水面AB与该桥拱的最高点P之间的距离是米，在离水面AB相同高度的C，D处安装两盛景观灯，若点C是 $\overset{⌢}{A P}$ 的中点，则点C离水面AB的距离是米．

查看试题解析

三、解答题（本题有8小题，共66分）

17. 如图，在每个小正方形的边长为1个单位的网格中，△ABC的顶点均在格点（网格线的交点）上．

⑴将△ABC向右平移5个单位得到△A₁B₁C₁ ，画出△A₁B₁C₁；

⑵将（1）中的△A₁B₁C₁绕点C₁逆时针旋转90°得到△A₂B₂C₁ ，画出△A₂B₂C₁ ．

查看试题解析
18. 在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机地摸取一个小球然后放回，再随机地摸出一个小球．

(1)、请你用树状图或列表法列出所有可能的结果；

(2)、求两次取出的小球标号和等于4的概率．

查看试题解析
19. 已知四边形ABCD内接于⊙O， $\overset{⌢}{A B}$ ＝ $\overset{⌢}{A C}$ ， ∠ADC＝120°，求证：△ABC是等边三角形．

查看试题解析
20. 《九章算术》是我国古代数学成就的杰出代表作，书中记载：“今有中，不知大小．以锯锯之，深1寸，锯道长1尺，问经几何？“其意思为：“如图，今有一圆形木材在墙中，不知其大小用锯子去锯这个木材，锯口深DE＝1寸，锯道长AB＝10寸，问这块圆形木材的直径是多少？”

查看试题解析
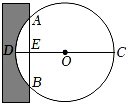21. 学完《概率初步》后，小诚和小明两个好朋友利用课外活动时间自制A、B两组卡片共5张，A组三张分别写有数字2，4，6，B组两张分别写有3，5．它们除了数字外没有任何区别．他俩提出了如下两个问题请你解答：

(1)、随机地分别从A组、B组各抽取一张，请你用列表或画树状图的方法表示所有等可能的结果；

(2)、如果他俩还制定这样一个游戏规则：若选出的两数之积为3的倍数，则小诚获胜；否则小明获胜．请问这样的游戏规则对小诚、小明双方公平吗？请说明理由．

查看试题解析
22. 如图，AB为⊙O的直径，CD为弦，CD⊥AB于点E，连接DO并延长交⊙O于点F，连接AF交CD于点G，CG＝AG，连接AC．

(1)、求证：AC∥DF；

(2)、若AB＝12，求AC和GD的长．

查看试题解析

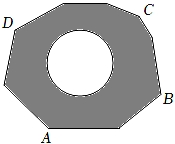
23. 如图，地面上有一个不规则的封闭图形ABCD，为求得它的面积，小明设计了一个如下方法：

①在此封闭图形内画出一个半径为1米的圆．

②在此封闭图形旁边闭上眼睛向封闭图形内掷小石子（可把小石子近似地看成点），记录如下：

掷小石子落在不规则图形内的总次数	50	150	300	500	…
小石子落在圆内（含圆上）的次数m	20	59	123	203	…
小石子落在圆外的阴影部分（含外缘）的次数n	29	91	176	293	…
m：n	0.689	0.694	0.689	0.706

(1)、通过以上信息，可以发现当投掷的次数很大时，则m：n的值越来越接近（结果精确到0.1）．

(2)、若以小石子所落的有效区域为总数（即m+n），则随着投掷次数的增大，小石子落在圆内（含圆上）的频率值稳定在附近（结果精确到0.1）．

(3)、请你利用（2）中所得频率的值，估计整个封闭图形ABCD的面积是多少平方米？（结果保留π）

查看试题解析

24. 如图1，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点.

(1)、观察猜想：
图1中，线段PM与PN的数量关系是，位置关系是；

(2)、探究证明：
把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；

(3)、拓展延伸：
把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值.

查看试题解析