山东省潍坊市青州市2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-11-10 类型:期中考试
一、单选题
-
1. 如图,有甲、乙、丙三个矩形,其中相似的是( )
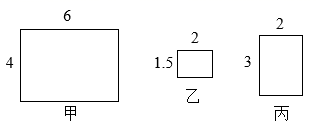 A、甲与丙 B、甲与乙 C、乙与丙 D、三个矩形都不相似2. 如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A、甲与丙 B、甲与乙 C、乙与丙 D、三个矩形都不相似2. 如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )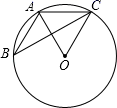 A、25° B、50° C、65° D、75°3. 如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,若OA:OA'=1:2,则△ABC与△A'B'C'的周长比为( )
A、25° B、50° C、65° D、75°3. 如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,若OA:OA'=1:2,则△ABC与△A'B'C'的周长比为( )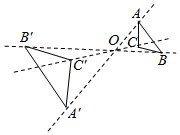 A、1:4 B、1:3 C、1:2 D、1:94. 如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A、1:4 B、1:3 C、1:2 D、1:94. 如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )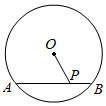 A、3.1 B、4.2 C、5.3 D、6.45. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )
A、3.1 B、4.2 C、5.3 D、6.45. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )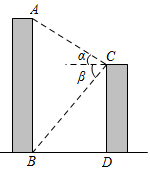 A、 B、 C、 D、6. 我国古代数学著作《九章算术》中的“井深”问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”,它的题意是:如图尺,尺,问井深是多少.如图,设井深为x尺,所列方程正确的是( )
A、 B、 C、 D、6. 我国古代数学著作《九章算术》中的“井深”问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”,它的题意是:如图尺,尺,问井深是多少.如图,设井深为x尺,所列方程正确的是( ) A、 B、 C、 D、7. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
A、 B、 C、 D、7. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
 A、 B、 C、 D、8. 如图,已知点A(-6,0),B(2,0),点C在直线 上,则使△ABC是直角三角形的点C的个数为( )
A、 B、 C、 D、8. 如图,已知点A(-6,0),B(2,0),点C在直线 上,则使△ABC是直角三角形的点C的个数为( )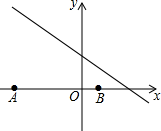 A、1 B、2 C、3 D、49. 如图,中,点D是边上一点,下列条件中,不能判定与相似的是( )
A、1 B、2 C、3 D、49. 如图,中,点D是边上一点,下列条件中,不能判定与相似的是( )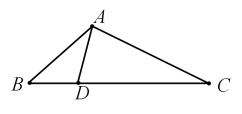 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
10. 在中,a,b,c分别是的对边, , 下列各式不一定成立的是( )A、 B、 C、 D、11. 如图,在正方形中,E,F分别是 , 的中点,交于点H,交于点G,下列结论正确的是( )
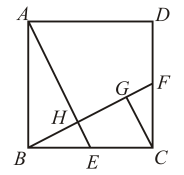 A、 B、 C、 D、12. 如图,AB是的直径,弦于点G,点F是CD上一点,且满足 , 连接AF并延长交于点E,连接AD、DE,若 . 下列结论正确的是( )
A、 B、 C、 D、12. 如图,AB是的直径,弦于点G,点F是CD上一点,且满足 , 连接AF并延长交于点E,连接AD、DE,若 . 下列结论正确的是( ) A、 B、 C、 D、DC平分
A、 B、 C、 D、DC平分三、填空题
-
13. 如图,将△ABC放在每个小正方形边长为1的网格中,点A,B,C均在格点上,则tanA的值是 .
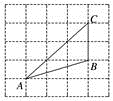 14. 如图,△ABC的三个顶点都在直角坐标系中的格点上,图中△ABC外接圆的圆心坐标是 .
14. 如图,△ABC的三个顶点都在直角坐标系中的格点上,图中△ABC外接圆的圆心坐标是 .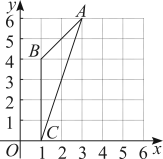 15. 如图,ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下AMN,则剪下的三角形的周长为 .
15. 如图,ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下AMN,则剪下的三角形的周长为 .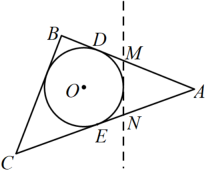 16. 如图,在平面直角坐标系中, , 连结并延长至C,连结 , 若满足 , , 则点C的坐标为 .
16. 如图,在平面直角坐标系中, , 连结并延长至C,连结 , 若满足 , , 则点C的坐标为 .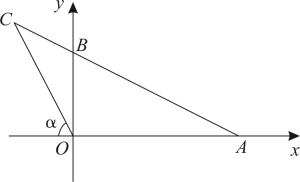
四、解答题
-
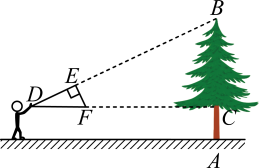
17. 计算:(1)、;(2)、 .18. 如图,小明同学用自制的直角三角形DEF测量树的高度AB,他调整自己的位置,设斜边DF保持水平,并且边DE与点B在同一直线,DE=0.4m,EF=0.3m,测得边DF离地面高度AC=1.5m,CD=10m,求树高AB.
 19. 如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证:
19. 如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证: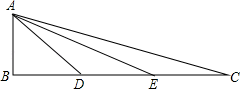 (1)、△ADE∽△CDA;(2)、∠C+∠AEB=45°.20. 请阅读以下材料,并完成相应的问题:
(1)、△ADE∽△CDA;(2)、∠C+∠AEB=45°.20. 请阅读以下材料,并完成相应的问题:角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则 .
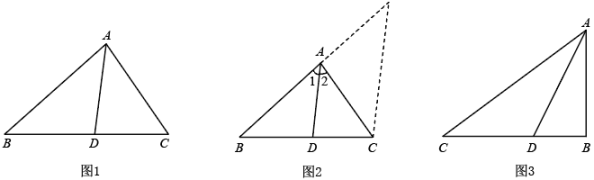
下面是这个定理的部分证明过程.
证明:如图2,过点C作 . 交BA的延长线于点E.…
任务:
(1)、请按照上面的证明思路,写出该证明过程的剩余部分;(2)、如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.21. 图1是停车场入口处的升降杆,当汽车刷牌照进入时,升降杆就会从水平位置升起.图2是其示意图,其中 , , , , , 现由于故障,不能完全升起,最大为 .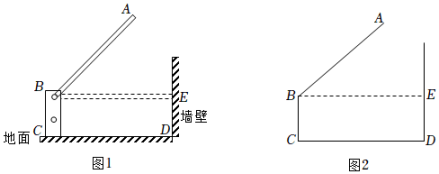 (1)、求故障时A点最高可距离地面多少m(精确到0.1m).(2)、若一辆箱式小货车宽1.8m,高2.4m,请问这辆车能否在升降杆故障时进入停车场?
(1)、求故障时A点最高可距离地面多少m(精确到0.1m).(2)、若一辆箱式小货车宽1.8m,高2.4m,请问这辆车能否在升降杆故障时进入停车场?(参考数据: , , )
22. 如图,在等腰中, , 以为直径的与交于点D, , 垂足为E,的延长线与的延长线交于点F.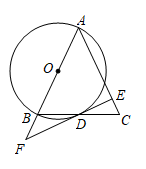 (1)、求证:是的切线;(2)、若的半径为 , , 求的长.23.(1)、【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.
(1)、求证:是的切线;(2)、若的半径为 , , 求的长.23.(1)、【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.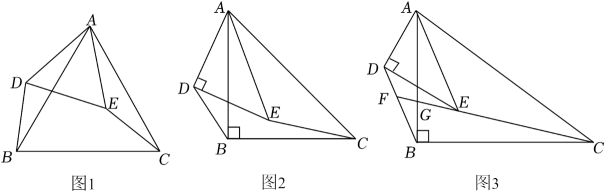 (2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.
(2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.①求的值;
②延长CE交BD于点F,交AB于点G.求sin∠BFC的值.