云南省楚雄彝族自治州双柏县2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-11-10 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 2 x = 0$ 的根是（）

A、 $x = 0$ B、 $x = 2$ C、 $x = 0$ 或 $x = 2$ D、 $x = \pm 2$

查看试题解析
2. 下列关于菱形的说法中正确的是（）

A、对角线互相垂直的四边形是菱形 B、菱形的对角线互相垂直且平分 C、菱形的对角线相等且互相平分 D、对角线互相平分的四边形是菱形

查看试题解析
3. 正方形具有而矩形不一定有的性质是（）

A、对角线互相垂直 B、对角线相等 C、对角互补 D、四个角相等

查看试题解析
4. 用配方法解一元二次方程x²﹣6x=﹣5的过程中，配方正确的是（　　）

A、（x+3）²=1 B、（x﹣3）²=1 C、（x+3）²=4 D、（x﹣3）²=4

查看试题解析
5. 有五张卡片的正面分别写有“喜”“迎”“二”“十”“大”，五张卡片洗匀后将其反面朝上放在桌面上，小明从中任意抽取两张卡片，恰好是“二十”的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{1}{20}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
6. 如图所示，已知矩形 $A B C D$ 的边 $A D$ 长为8cm，边 $A B$ 长为6cm，从中截去一个矩形（图中阴影部分），如果所截矩形与原矩形相似，那么所截矩形的面积是（）

A、21cm² B、24cm² C、27cm² D、30cm²

查看试题解析
7. 已知线段 $a = 2$ ， $b = 3$ ， $c = 4$ ，如果线段 $a$ ， $b$ ， $c$ ， $d$ 成比例，则线段d的长为（）

A、2 B、3 C、4 D、6

查看试题解析
8. 已知关于x的方程x²+3x+a=0有一个根为﹣2，则另一个根为（　　）

A、5 B、﹣1 C、2 D、﹣5

查看试题解析
9. 等边三角形的一边与这边上的高的比是（）

A、 $\sqrt{3}$ ：2 B、 $\sqrt{3}$ ：1 C、2： $\sqrt{3}$ D、1： $\sqrt{3}$

查看试题解析
10. 如图，已知点D是 $△ A B C$ 的边 $A C$ 上的一点，根据下列条件，可以得到 $△ A B C ∼ △ B D C$ 的是（）

A、 $A B \cdot C D = B D \cdot B C$ B、 $A C \cdot C B = C A \cdot C D$ C、 $B C^{2} = A C \cdot D C$ D、 $B D^{2} = C D \cdot D A$

查看试题解析
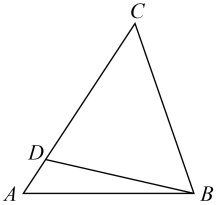11. 某电视机厂计划两年后产量为现在的2倍，如果每年增长率为x，则可得方程（）

A、 ${(1 + x)}^{2} = 2$ B、 $1 + x = 2$ C、 $1 + 2 x = 2$ D、 ${(1 + x)}^{2} = 3$

查看试题解析
12. 如图，AB是斜靠在墙上的梯子，梯脚距墙2米，梯子上的点D距墙1.8米，BD长0.6米，则梯子的长为（）

A、5.6米 B、6米 C、6.1米 D、6.2米

查看试题解析

二、填空题

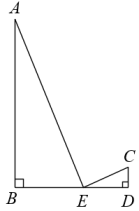
13. 一个菱形的两条对角线长分别为7cm和8cm，则这个菱形面积为．

查看试题解析
14. 已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 2 x - 1 = 0$ 的两根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}} =$ ．

查看试题解析
15. 若关于x的方程x²－2x＋m＝0有实数根，则m的取值范围为；

查看试题解析
16. 已知 $\frac{x}{y} = \frac{2}{3}$ ，则 $\frac{2 x - y}{y}$ ＝．

查看试题解析
17. 一副扑克牌去掉大小王后，只剩下52张牌，从中任取一张，记下花色，随着试验次数的增加，出现红桃花色的频率将稳定在左右．

查看试题解析
18. 如图所示， $A B ⊥ B D$ 于点B， $C D ⊥ B D$ 于点D， $A B = 9 ， C D = 1 ， B D = 6$ ，点E在 $B D$ 上移动，当以 $E ， C ， D$ 为顶点的三角形与 $△ A B E$ 相似时，求 $D E$ 的长为．

查看试题解析

三、解答题

19. 用适当的方法解下列方程：

(1)、 $x^{2} - 4 x + 2 = 0$

(2)、 $3 x (1 - x) = 2 x - 2$

查看试题解析
20. 深圳市某商场销售某女款上衣，刚上市时每件可盈利100元，销售一段时间后开始滞销，经过连续两次降价后，每件盈利为81元，平均每天可售出20件．

(1)、求平均每次降价盈利的百分率；

(2)、为扩大销售量，尽快减少库存，在“双十一”期间该商场决定再次采取适当的降价措施，经调查发现，一件女款上衣每降价1元，每天可多售出2件．若商场每天要盈利2940元，每件应降价多少元？

查看试题解析
21. 小李和小王两位同学做游戏，在一个不透明的口袋中放入1个红球、2个白球、1个黑球，这些球除颜色外都相同，将球摇匀.

(1)、从中任意摸出1个球，恰好摸到红球的概率是多少?

(2)、两人约定：从袋中一次摸出两个球，若摸出的两个球是-红一黑，则小李获胜：若摸出的两个球都是白色，则小王获胜，请用列举法（画树状图或列表）分析游戏规则是否公平.

查看试题解析
22. 如图，在▱ABCD中，对角线AC，BD相交于点O，且OA=OB．

(1)、求证：四边形ABCD是矩形；

(2)、若AD=4，∠AOD=60°，求AB的长．

查看试题解析
23. 如图，在菱形ABCD中，对角线AC和BD交于点O，E为AB上一动点，过点E作EF∥BD交AD于点F，连接BF、DE．

(1)、若∠ABD＝40°，求∠CAD的度数；

(2)、求证：BF＝DE．

查看试题解析
24. 如图，已知矩形 $D E F G$ 的边 $D E$ 在 $△ A B C$ 的边 $B C$ 上，顶点G，F分别在边 $A B$ ， $A C$ 上． $△ A B C$ 的高 $A H$ 交 $G F$ 于点I．

(1)、求证： $B D \cdot E H = D H \cdot C E$ ；

(2)、设 $D E = n \cdot E F$ （n为正实数），求证： $\frac{n}{B C} + \frac{1}{A H} = \frac{1}{E F}$ ．

查看试题解析