山东省威海市乳山市2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-11-10 类型:期中考试
一、单选题
-
1. 若反比例函数 的图象经过点 ,则该反比例函数的图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限2. 在Rt△ABC中,∠C=90°,若sin∠A= , 则cosB=( )A、 B、 C、 D、3. 关于抛物线 , 下列说法错误的是( )A、开口向上 B、顶点坐标为 C、当时,y随x的增大而增大 D、该抛物线与x轴有两个交点4. 在中,、均为锐角,且 , 则是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形5. 已知点 , , 在反比例函数的图像上,则y1 ,y2的大小关系为( )A、 B、 C、 D、无法判断6. 把抛物线的图像向右平移3个单位,再向上平移2个单位,所得到的图像的解析式为 , 则( )A、2 B、4 C、6 D、87. 二次函数和反比例函数在同一直角坐标系中的大致图象是( )A、
 B、
B、 C、
C、 D、
D、 8. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,10时到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么船在B处时与小岛M的距离( )
8. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,10时到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么船在B处时与小岛M的距离( )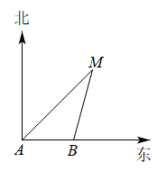 A、海里 B、海里 C、40海里 D、海里9. 如图,四边形是边长为1的正方形,与x轴正半轴的夹角为 , 点B在抛物线()的图象上,则( )
A、海里 B、海里 C、40海里 D、海里9. 如图,四边形是边长为1的正方形,与x轴正半轴的夹角为 , 点B在抛物线()的图象上,则( ) A、-2 B、 C、 D、10. 已知二次函数()的图像如图所示,顶点为则下列结论:
A、-2 B、 C、 D、10. 已知二次函数()的图像如图所示,顶点为则下列结论:①;②; ③;④ .
其中正确结论的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,直线过点 , 则 .
 12. 反比例函数的图象如图所示,点A在该函数图象上,AB垂直于x轴,垂足为点B,如果 , 那么k= .
12. 反比例函数的图象如图所示,点A在该函数图象上,AB垂直于x轴,垂足为点B,如果 , 那么k= .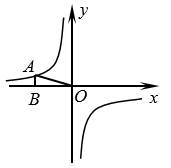 13. 小丽想测量学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为30°,测倾器到旗杆底部的距离为12米,测倾器的高度为1.6米,那么旗杆的高度为米(结果保留根号).
13. 小丽想测量学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为30°,测倾器到旗杆底部的距离为12米,测倾器的高度为1.6米,那么旗杆的高度为米(结果保留根号). 14. 反比例函数与正比例函数的一个交点为 , 则关于x的方程的解为 .15. 二次函数 , 当时,y随着x的增大而减小,当时,y随着x的增大而增大,则k= .16. 如图,的顶点A在抛物线上, , , . 将绕点O顺时针旋转 , 得到 , 边与该抛物线交于点P,则点P的坐标为.
14. 反比例函数与正比例函数的一个交点为 , 则关于x的方程的解为 .15. 二次函数 , 当时,y随着x的增大而减小,当时,y随着x的增大而增大,则k= .16. 如图,的顶点A在抛物线上, , , . 将绕点O顺时针旋转 , 得到 , 边与该抛物线交于点P,则点P的坐标为.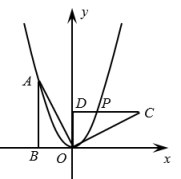
三、解答题
-
17. 计算: .18. 如图,一次函数与反比例函数的图像交于 和;
 (1)、求一次函数及反比例函数的表达式;(2)、根据图像,直接写出关于x的不等式的解集.19. 某商场购进一批单价为40元的商品,若按每件50元销售,平均每天可销售90件.市场调查发现,这种商品的销售单价每提高1元,平均每天少销售3件.将销售单价定为多少,才能使每天所获销售利润W最大?最大利润W是多少?20. 将一副三角板如图摆放,使三角板的45°角的顶点A与三角板的直角顶点D重合,且点E在上.若 , , 求的长.(结果保留根号)
(1)、求一次函数及反比例函数的表达式;(2)、根据图像,直接写出关于x的不等式的解集.19. 某商场购进一批单价为40元的商品,若按每件50元销售,平均每天可销售90件.市场调查发现,这种商品的销售单价每提高1元,平均每天少销售3件.将销售单价定为多少,才能使每天所获销售利润W最大?最大利润W是多少?20. 将一副三角板如图摆放,使三角板的45°角的顶点A与三角板的直角顶点D重合,且点E在上.若 , , 求的长.(结果保留根号) 21. 一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点A处观测到河对岸有一点C在A的南偏西60°的方向上,沿河岸向西前行20m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度.(结果保留根号)
21. 一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点A处观测到河对岸有一点C在A的南偏西60°的方向上,沿河岸向西前行20m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度.(结果保留根号) 22. 如图,点A在双曲线y= (x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.
22. 如图,点A在双曲线y= (x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.
 23. 乒乓球台的横截面如图所示,桌面长 , 位于球桌中线的球网高 , 以的延长线上距A点23cm的O点为坐标原点,所在的直线为x轴,建立如图所示的坐标系.从O点发出的球经过点 , 且路径是抛物线的一部分,在距O点水平距离为100cm的地方,球达到最高点.
23. 乒乓球台的横截面如图所示,桌面长 , 位于球桌中线的球网高 , 以的延长线上距A点23cm的O点为坐标原点,所在的直线为x轴,建立如图所示的坐标系.从O点发出的球经过点 , 且路径是抛物线的一部分,在距O点水平距离为100cm的地方,球达到最高点. (1)、求抛物线的解析式;(2)、此球是否可以击中球台且不触网?请说明理由.24. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B.抛物线过A,B两点,与x轴的另一个交点为C, .
(1)、求抛物线的解析式;(2)、此球是否可以击中球台且不触网?请说明理由.24. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B.抛物线过A,B两点,与x轴的另一个交点为C, .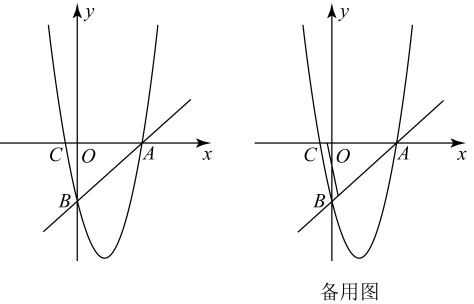 (1)、求抛物线的表达式;(2)、若点P为抛物线的顶点,求四边形的面积;(3)、抛物线上是否存在点Q,使得是以为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.
(1)、求抛物线的表达式;(2)、若点P为抛物线的顶点,求四边形的面积;(3)、抛物线上是否存在点Q,使得是以为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.