山东省青岛市市北区2022-2023学年九年级上学期期中考试数学试题
试卷更新日期:2022-11-10 类型:期中考试
一、单选题
-
1. 下列方程中,关于x的一元二次方程是( )A、 B、 C、 D、2. 如果 则 等于( )A、 B、 C、 D、63. 方程x2-2x-24=0的根是( )A、x1=6,x2=4 B、x1=6,x2=-4 C、x1=-6,x2=4 D、x1=-6,x2=-44. 要检验一张四边形的纸片是否为菱形,下列方案中可行的是( )A、度量四个内角是否相等 B、测量两条对角线是否相等 C、测量两条对角线的交点到四个顶点的距离是否相等 D、将这纸片分别沿两条对角线对折,看对角线两侧的部分是否每次都完全重合5. 如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B等于( )
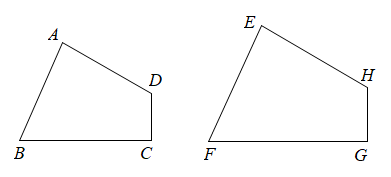 A、55° B、65° C、75° D、85°6. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则正确的方程是( )A、 B、 C、 D、7. 如图,正方形边长为1,以为边作第2个正方形 , 再以为边作第3个正方形 , ……,按照这样的规律作下去,第2022个正方形的边长为( )
A、55° B、65° C、75° D、85°6. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则正确的方程是( )A、 B、 C、 D、7. 如图,正方形边长为1,以为边作第2个正方形 , 再以为边作第3个正方形 , ……,按照这样的规律作下去,第2022个正方形的边长为( ) A、 B、 C、 D、8. 如图,平行四边形中,过A作于M,交BD于E,过C作于N,交BD于F,连结AF、CE,则下列结论中正确的个数是( )
A、 B、 C、 D、8. 如图,平行四边形中,过A作于M,交BD于E,过C作于N,交BD于F,连结AF、CE,则下列结论中正确的个数是( )①;②四边形是平行四边形;③当时,四边形是菱形;④当M、N分别是中点时,四边形是正方形;
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
9. 已知点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC=.10. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有20个,除颜色外其他完全相同,通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在20%和50%,则口袋中白色球的个数可能是个.11. 某商品经过连续两次降价,售价由原来的25元/件降到16元/件,则平均每次降价的百分率为.12. 为做好疫情防控工作,某学校门口设置了A,B两条体温快速检测通道,该校两名互不相识的同学王明和李强,随机进入学校,二人恰好均从A通道入校的概率是 .13. 若关于x的一元二次方程有两个不相等的实数根,则m的取值范围是 .14. 如图,为了测量旗杆的高度,某综合实践小组设计了以下方案:用2.5m长的竹竿做测量工具,移动竹竿,保持竹竿与旗杆平行,使竹竿、旗杆的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距5m、与旗杆相距20m,则旗杆的高度为m.
 15. 如图,正方形的边长为3,E是边上一点, ,将沿折叠到 , 延长交于点F.过点E作 , 交于点P,交的延长线于点H,则= .
15. 如图,正方形的边长为3,E是边上一点, ,将沿折叠到 , 延长交于点F.过点E作 , 交于点P,交的延长线于点H,则= . 16. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是矩形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=4,b=2,则矩形ABCD的面积是 .
16. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是矩形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=4,b=2,则矩形ABCD的面积是 .
三、解答题
-
17. 用圆规、直尺作图,不写作法,但到保留作图痕迹.
已知:线段a,
求作:正方形ABCD,使其对角线AC=a.
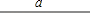 18. 用合适的方法解下列方程(1)、(2)、19. 如图,四边形是平行四边形,E为线段延长线上一点,连结交对角线于点F, .
18. 用合适的方法解下列方程(1)、(2)、19. 如图,四边形是平行四边形,E为线段延长线上一点,连结交对角线于点F, . (1)、求证:;(2)、如果 , 则=度.20. 如图,两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字2,0,;转盘B被四等分,分别标有数字3,2,-2,-3.如果同时任意转动转盘A、B,转盘停止时,两个指针指向转盘A、B上的对应数字分别为x,y(指针指在两个扇形的交线时,重新转动转盘).小红和小兰用这两个转盘做游戏,若x与y的乘积是正数,则小红赢;若x与y的乘积是负数,则小兰赢.这个游戏对双方公平吗?请借助画树状图或列表的方法说明理由.
(1)、求证:;(2)、如果 , 则=度.20. 如图,两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字2,0,;转盘B被四等分,分别标有数字3,2,-2,-3.如果同时任意转动转盘A、B,转盘停止时,两个指针指向转盘A、B上的对应数字分别为x,y(指针指在两个扇形的交线时,重新转动转盘).小红和小兰用这两个转盘做游戏,若x与y的乘积是正数,则小红赢;若x与y的乘积是负数,则小兰赢.这个游戏对双方公平吗?请借助画树状图或列表的方法说明理由.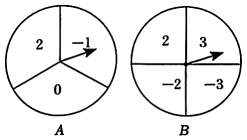 21. 如图,矩形矩形 , 与相交于G,与相交于H. 请判断并证明四边形的形状.
21. 如图,矩形矩形 , 与相交于G,与相交于H. 请判断并证明四边形的形状. 22. 某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查发现,售价在40元至60元之间,这种台灯的售价每上涨1元,其销售量就将减少10个.(1)、若y(个)表示这种台灯平均每月的销量,x(元)表示这种台灯的售价,求y与x的函数关系式;(2)、为了实现平均每月12000元的销售利润,求这种台灯的售价应定为多少元.23. 如图,在矩形 中, , E是上一点,且 ,动点P从点B出发,沿方向以每秒3个单位的速度向点C运动,动点Q从点D出发,沿向以每秒1个单位的速度向点A运动,过点P作 交于点F,过点F作 交于点G,连接 . 当点F与点A重合时,点P、Q同时停止运动,设点P的运动时间为t秒.
22. 某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查发现,售价在40元至60元之间,这种台灯的售价每上涨1元,其销售量就将减少10个.(1)、若y(个)表示这种台灯平均每月的销量,x(元)表示这种台灯的售价,求y与x的函数关系式;(2)、为了实现平均每月12000元的销售利润,求这种台灯的售价应定为多少元.23. 如图,在矩形 中, , E是上一点,且 ,动点P从点B出发,沿方向以每秒3个单位的速度向点C运动,动点Q从点D出发,沿向以每秒1个单位的速度向点A运动,过点P作 交于点F,过点F作 交于点G,连接 . 当点F与点A重合时,点P、Q同时停止运动,设点P的运动时间为t秒. (1)、=(用含t的代数式表示);t的取值范围是;(2)、是否存在某一时刻t,使得若存在,求出此时t的值;若不存在,请说明理由;(3)、连接 、 ,是否存在某一时刻t,使在同一直线上?若存在,求出t的值;若不存在,说明理由.24. 定义:在平面直角坐标系中,对于任意两点 ,若点 满足 ,那么称点T是点A,B的“相似点”.
(1)、=(用含t的代数式表示);t的取值范围是;(2)、是否存在某一时刻t,使得若存在,求出此时t的值;若不存在,请说明理由;(3)、连接 、 ,是否存在某一时刻t,使在同一直线上?若存在,求出t的值;若不存在,说明理由.24. 定义:在平面直角坐标系中,对于任意两点 ,若点 满足 ,那么称点T是点A,B的“相似点”.例如: ,当 满足 时,则点 是点A,B的“相似点”.
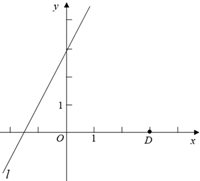 (1)、已知点 ,请说明其中一个点是另外两个点的“相似点”.(2)、如图,点 在x轴上,点 是直线l上任意一点,点 是点D,E的“相似点”.
(1)、已知点 ,请说明其中一个点是另外两个点的“相似点”.(2)、如图,点 在x轴上,点 是直线l上任意一点,点 是点D,E的“相似点”.①试确定y与x的关系式.
②若直线 交x轴于点H,当 为直角三角形时,请直接写出点E的坐标.