山东省青岛市市北区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-11-10 类型:期中考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC相似的是( )
 A、
A、 B、
B、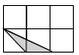 C、
C、 D、
D、 3. 一个不透明的袋子中装有3个红球和1个黄球,这些球除颜色外完全相同,从袋子中随机摸出两个球,摸出的两个球颜色相同的概率是( )A、 B、 C、 D、4. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
3. 一个不透明的袋子中装有3个红球和1个黄球,这些球除颜色外完全相同,从袋子中随机摸出两个球,摸出的两个球颜色相同的概率是( )A、 B、 C、 D、4. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( ) A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE5. 输入一组数据,按下列程序进行计算,输出结果如表:
A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE5. 输入一组数据,按下列程序进行计算,输出结果如表:x
20.5
20.6
20.7
20.8
20.9
输出
-13.75
-8.04
-2.31
3.44
9.21
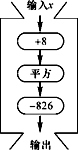
分析表格中的数据,估计方程(x+8)2-826=0的一个正数解x的大致范围为( )
A、20.5<x<20.6 B、20.6<x<20.7 C、20.7<x<20.8 D、20.8<x<20.96. 如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AB,BC边上的中点,连接EF.若 ,BD=4,则菱形ABCD的周长为( ) A、4 B、 C、 D、287. 如图所示,要建一个面积为的仓库,并在与墙平行的一边开一道宽的门,仓库有一边靠墙(墙长),围建仓库的材料共有长,则仓库的长是( )
A、4 B、 C、 D、287. 如图所示,要建一个面积为的仓库,并在与墙平行的一边开一道宽的门,仓库有一边靠墙(墙长),围建仓库的材料共有长,则仓库的长是( ) A、 B、 C、 D、或8. 如图,点在菱形的边上,点在边的延长线上, , , 则下列结论正确的有( )个.
A、 B、 C、 D、或8. 如图,点在菱形的边上,点在边的延长线上, , , 则下列结论正确的有( )个.①;②;③;④
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
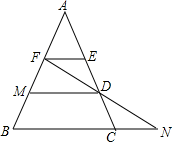
9. 若 , 则 .10. 已知关于x的一元二次方程x2﹣4x+m=0有一个根为1,则方程的另一个根为.11. 已知,如图在中, , , 的延长线交的延长线于 , 则为 .
 12. 在一个不透明的袋子中有若干个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:
12. 在一个不透明的袋子中有若干个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:摸球实验次数
100
1000
5000
10000
50000
100000
“摸出黑球”的次数
36
387
2019
4009
19970
40008
“摸出黑球”的频率
(结果保留小数点后三位)
0.360
0.387
0.404
0.401
0.399
0.400
根据试验所得数据,估计“摸出黑球”的概率是(结果保留小数点后一位).
13. 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为度. 14. 如图,是边长为3的正方形的对角线,在上,且 , 连接 , 点是上一个动点,于点 , 于点 , 则的值是 .
14. 如图,是边长为3的正方形的对角线,在上,且 , 连接 , 点是上一个动点,于点 , 于点 , 则的值是 . 15. 某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为 .16. 如图,正方形中,、是线段上的点,且 , 点在线段上,且 , 、分别交于点和 , 以下说法中正确的有 . (请填写序号)
15. 某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为 .16. 如图,正方形中,、是线段上的点,且 , 点在线段上,且 , 、分别交于点和 , 以下说法中正确的有 . (请填写序号)①;②;③;④

三、解答题
-
17. 用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:线段a和∠α.
求作:菱形ABCD,使菱形ABCD的边长为a,其中一个内角等于∠α.
 18. 计算:(1)、(配方法).(2)、 .(3)、 .(4)、若关于的方程有两个相等的实数根,求的值.19. 游戏者用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于3,则游戏者获胜.
18. 计算:(1)、(配方法).(2)、 .(3)、 .(4)、若关于的方程有两个相等的实数根,求的值.19. 游戏者用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于3,则游戏者获胜. (1)、利用画树状图或列表的方法表示游戏所有可能出现的结果;(2)、求游戏者获胜的概率.20. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、利用画树状图或列表的方法表示游戏所有可能出现的结果;(2)、求游戏者获胜的概率.20. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.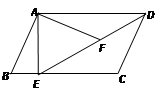 (1)、求证:△ADF∽△DEC(2)、若AB=4,AD=3 ,AE=3,求AF的长.21. 我市茶叶专卖店销售某品牌茶叶,其进价为每千克240元,按每千克400元出售,平均每周可售出200千克,后来经过市场调查发现,单价每降低10元,则平均每周的销售量可增加40千克.(1)、当销售单价定为每千克340元时,请计算每周销售量和销售利润.(2)、若该专卖店销售这种品牌茶叶要想平均每周获利41600元,并尽可能让利于顾客,赢得市场,每千克茶叶应降价多少元?22. 如图,在▱ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD.
(1)、求证:△ADF∽△DEC(2)、若AB=4,AD=3 ,AE=3,求AF的长.21. 我市茶叶专卖店销售某品牌茶叶,其进价为每千克240元,按每千克400元出售,平均每周可售出200千克,后来经过市场调查发现,单价每降低10元,则平均每周的销售量可增加40千克.(1)、当销售单价定为每千克340元时,请计算每周销售量和销售利润.(2)、若该专卖店销售这种品牌茶叶要想平均每周获利41600元,并尽可能让利于顾客,赢得市场,每千克茶叶应降价多少元?22. 如图,在▱ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD. (1)、求证:△ADE≌△CBF.(2)、若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.23. 阅读理解:
(1)、求证:△ADE≌△CBF.(2)、若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.23. 阅读理解:如图1,在四边形的边上任取一点E(点E不与点A、点B重合),分别连接 , , 可以把四边形分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形的边上的相似点;如果这三个三角形都相似,我们就把E叫做四边形的边上的强相似点.
 (1)、如图1, , 试判断点E是否是四边形的边上的相似点,并说明理由;(2)、如图2,在矩形中,四点均在正方形网格(网格中每个最小正方形的边长为1)的格点(即每个最小正方形的顶点)上,若图2中,矩形的边上存在强相似点E,则;(3)、 拓展探究:
(1)、如图1, , 试判断点E是否是四边形的边上的相似点,并说明理由;(2)、如图2,在矩形中,四点均在正方形网格(网格中每个最小正方形的边长为1)的格点(即每个最小正方形的顶点)上,若图2中,矩形的边上存在强相似点E,则;(3)、 拓展探究:如图3,将矩形沿折叠,使点落在边上的点E处.若点E恰好是四边形的边上的一个强相似点,试探究和的数量关系.
24. 在平面直角坐标系中,已知 , , 点从点开始沿边向点以的速度移动;点从点开始沿边向点以的速度移动.如果、同时出发,用表示移动的时间 . (1)、用含的代数式表示:线段cm;cm.(2)、求当为何值时,四边形的面积为 .(3)、当与相似时,求出的值.(4)、求当为何值时,线段分三角形的面积比为 .
(1)、用含的代数式表示:线段cm;cm.(2)、求当为何值时,四边形的面积为 .(3)、当与相似时,求出的值.(4)、求当为何值时,线段分三角形的面积比为 .