山东省青岛市莱西市2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-11-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四幅图，表示两棵树在同一时刻阳光下的影子是（）

A、 B、 C、 D、

查看试题解析
2. 函数 $y = \frac{\sqrt{x} - 2}{x - 3}$ 的自变量x的取值范围是（）

A、 $x \neq 3$ B、 $x > 0$ 且 $x \neq 3$ C、 $x \geq 0$ 且 $x \neq 3$ D、 $x \geq 2$ 且 $x \neq 3$

查看试题解析
3. 某商场的休息椅如图所示，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 在 $△ A B C$ 中， $∠ C = 90 °$ ，如果 $s i n A = \frac{3}{5}$ ，那么 $t a n A$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{5}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{3}$

查看试题解析
5. 如图， $A_{1} B_{1}$ 是线段AB在投影面P上的正投影， $A B = 20 c m$ ， $∠ A B B_{1} = 70 °$ ，则投影 $A_{1} B_{1}$ 的长为（）

A、 $20 s i n 70 ° c m$ B、 $20 c o s 70 ° c m$ C、 $20 t a n 70 ° c m$ D、 $\frac{20}{s i n 70 °} c m$

查看试题解析
6. 已知二次函数 $y = a x^{2} + b x - c (a \neq 0)$ ，其中 $b > 0$ 、 $c > 0$ ，则该函数的图象可能为（）

A、 B、 C、 D、

查看试题解析
7. 抛物线 $y = a x^{2} + b x + c$ 上部分点的横坐标 $x$ ，纵坐标 $y$ 的对应值如下表：
$x$
…
-2
-1
0
1
2
…
$y$
…
0
4
6
6
4
…
则下列说法中正确的个数是（）
①方程 $a x^{2} + b x + c = 0$ 有两根为 $x_{1} = - 2$ ， $x_{2} = 3$ ；②抛物线与y轴的交点为 $(0 ， 6)$ ；③抛物线的对称轴是直线 $x = 1$ ；④抛物线开口向上；

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 ° ， A B = 2 B C = 4$ ，动点P从点A出发，以每秒1个单位长度的速度沿线段 $A B$ 匀速运动，当点P运动到点B时，停止运动，过点P作 $P Q ⊥ A B$ 交 $A C$ 于点Q，将 $△ A P Q$ 沿直线 $P Q$ 折叠得到 $△ A^{'} P Q$ ，设动点P的运动时间为t秒， $△ A^{'} P Q$ 与 $△ A B C$ 重叠部分的面积为S，则下列图象能大致反映S与t之间函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 下列函数：① $y = - 5 x$ ；② $y = 3 x - 2$ ；③ $y = - \frac{3}{x} (x > 0)$ ；④ $y = 3 x^{2} (x < 0)$ ，其中y的值随x的增大而增大的函数为．（填序号）

查看试题解析
10. 如图， $△ A B C$ 的顶点是正方形网格的格点，则 $c o s ∠ B A C$ 的值为．

查看试题解析
11. △ABC中，∠A、∠B均为锐角，且 $| \tan B - \sqrt{3} | + {(2 \sin A - \sqrt{3})}^{2} = 0$ ，则△ABC的形状是．

查看试题解析
12. 若将抛物线 $y = a x^{2} - 4$ 向右平移3个单位，经过 $(2 ， - 6)$ ，则 $a$ 的值是．

查看试题解析
13. 一配电房示意图如图所示，它是一个轴对称图形．已知 $B C = 6 m$ ， $∠ A B C = 50 °$ ，则房顶A离地面EF的高度为m．（结果精确到 $0.1 m$ ，参考数据： $s i n 50 ° \approx 0.77$ ， $c o s 50 ° \approx 0.64$ ， $t a n 50 ° \approx 1.19$ ）

查看试题解析
14. 如图，这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图，则它的左视图的面积是．

查看试题解析

三、解答题

15. 计算

(1)、 $\frac{c o s 30 ° - t a n 60 ° \cdot c o s 45 °}{c o s 30 °}$

(2)、 $c o s 60 ° - 2 s i n^{2} 45 ° + \frac{3}{2} t a n^{2} 30 ° - s i n 30 °$

查看试题解析
16. 如图是两根木杆及其影子的图形.

(1)、这个图形反映的是中心投影还是平行投影?答：

(2)、请你在图中画出表示小树影长的线段AB.

查看试题解析
17. 如图，△ABC中，AD⊥BC，垂足是D，若BC=14，AD=12，tan∠BAD= $\frac{3}{4}$ ，求sinC的值．

查看试题解析
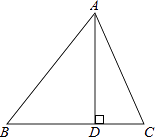18. 如图，小欣站在灯光下，投在地面上的身影 $A B = 2.4 m$ ，蹲下来，则身影 $A C = 1.05 m$ ，已知小明的身高 $A D = 1.6 m$ ，蹲下时的高度等于站立高度的一半，求灯离地面的高度 $P H$ ．

查看试题解析
19. 某学校升气球庆祝党的二十大胜利召开．如图，一气球到达离地面高度为12米的 $A$ 处时，仪器显示正前方一高楼顶部 $B$ 的仰角是 $37 °$ ，底部 $C$ 的俯角是 $60 °$ ．气球要飞到楼顶，应至少再上升多少米？（结果精确到0.1米）（参考数据： $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
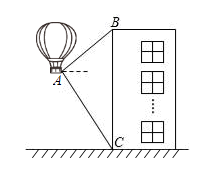20. 已知二次函数 $y = - \frac{1}{2} x^{2} + b x + c$ 的图象经过 $A (0 ， - 8)$ ， $B (- 2 ， - 20)$ 两点．

(1)、求b，c的值；

(2)、二次函数 $y = - \frac{1}{2} x^{2} + b x + c$ 的图象与x轴是否有公共点？若有，求公共点的坐标；若没有，请说明理由．

查看试题解析
21. 九年级二班学生到某劳动教育实践基地开展实践活动，当天，他们先从基地门口A处向正北方向走了220米，到达菜园B处锄草，再从B处沿正西方向走了200米，到达果园C处采摘水果，再向南偏东37°方向走了200米，到达手工坊D处进行手工制作，最后从D处回到门口A处．

(1)、求从手工坊D处回到门口A处的距离．

(2)、求从手工坊D处回到门口A处的方位角．[参考数据： $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ]

查看试题解析
22. 某超市经销一种商品，每千克成本为50元，经试销发现，该种商品每天销售量 $y$ （千克）与销售单价 $x$ （元/千克）满足一次函数关系，其每天销售单价、销售量的四组对应值如下表所示：

销售单价 $x$ （元/千克）

55

60

65

70

销售量 $y$ （千克）

70

60

50

40

(1)、求 $y$ （千克）与 $x$ （元/千克）之间的函数表达式；

(2)、当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？

查看试题解析
23. 如图1是一架菱形风筝，它的骨架由如图2的4条竹棒AC，BD，EF，GH组成，其中E，F，G，H分别是菱形 $A B C D$ 四边的中点，现有一根长为 $80 c m$ 的竹棒，正好锯成风筝的四条骨架，设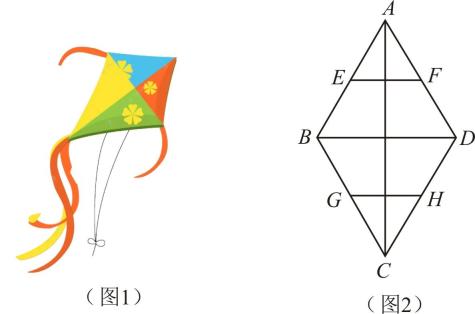 $A C ＝ x c m ，$ 菱形 $A B C D$ 的面积为 $y c m^{2}$ .

(1)、写出y关于 $x$ 的函数关系式：

(2)、为了使风筝在空中有较好的稳定性，要求 $25 c m \leq A C \leq \frac{4}{3} B D$ ，那么当骨架 $A C$ 的长为多少时，这风筝即菱形 $A B C D$ 的面积最大？此时最大面积为多少？

查看试题解析
24. 如图，二小球从斜坡A点处抛出，正好穿过B点的篮筐，落在斜坡底部的O点，以O为坐标原点建立直角坐标系，B的坐标为 $(\frac{1}{2} ， \frac{7}{8})$ ，斜坡的坡比为 $1 ： 2$ ， A点距地面的高度为1.5米，球的抛出路线可以用二次函数刻画．

(1)、求二次函数的表达式；

(2)、求小球到达的最高点的坐标．

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x - 3 (a \neq 0)$ 与x轴交于点 $A (- 1 ， 0)$ ，点 $B (3 ， 0)$ ，与y轴交于点C．

(1)、求抛物线的表达式；

(2)、在对称轴上找一点Q，使 $△ A C Q$ 的周长最小，求点Q的坐标；

(3)、P是第四象限内抛物线上的动点，求 $△ B P C$ 面积S的最大值及此时P点的坐标．

查看试题解析

销售单价 $x$ （元/千克）	55	60	65	70
销售量 $y$ （千克）	70	60	50	40

$x$	…	-2	-1	0	1	2	…
$y$	…	0	4	6	6	4	…