山东省济南市长清区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-11-10 类型:期中考试
一、单选题
-
1. 一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是( )
 A、
A、 B、
B、 C、
C、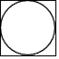 D、
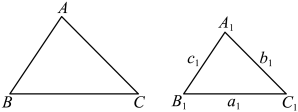
D、 2. 方程(x﹣2)(x+3)=0的两根分别是( )A、x1=﹣2,x2=3 B、x1=2,x2=3 C、x1=﹣2,x2=﹣3 D、x1=2,x2=﹣33. 已知 , 则的值为( )A、 B、 C、 D、4. 如图,直线 , 直线AC和DF被、、所截, , , , 则的长为( )
2. 方程(x﹣2)(x+3)=0的两根分别是( )A、x1=﹣2,x2=3 B、x1=2,x2=3 C、x1=﹣2,x2=﹣3 D、x1=2,x2=﹣33. 已知 , 则的值为( )A、 B、 C、 D、4. 如图,直线 , 直线AC和DF被、、所截, , , , 则的长为( ) A、12 B、3 C、 D、55. 如图,以点O为位似中心,作四边形的位似图形 , 已知 , 四边形的面积是2,则四边形的面积是( )
A、12 B、3 C、 D、55. 如图,以点O为位似中心,作四边形的位似图形 , 已知 , 四边形的面积是2,则四边形的面积是( )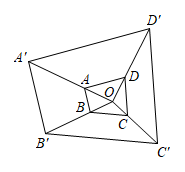 A、4 B、6 C、8 D、186. 已知是线段的黄金分割点, , 若 , 则( )A、 B、 C、 D、7. 如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在外选一点C,在、上分别找点M,N,使得 , , 测量出的长为 , 由此可知A、B间的距离为( )
A、4 B、6 C、8 D、186. 已知是线段的黄金分割点, , 若 , 则( )A、 B、 C、 D、7. 如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在外选一点C,在、上分别找点M,N,使得 , , 测量出的长为 , 由此可知A、B间的距离为( ) A、 B、 C、 D、8. 某厂家今年一月份的口罩产量是30万个,三月份的口罩产量是50万个,若设该厂家一月份到三月份的口罩产量的月平均增长率为x.则所列方程为( )A、30(1+x)2=50 B、30(1﹣x)2=50 C、30(1+x2)=50 D、30(1﹣x2)=509. 如图,是矩形的对角线,分别以点A,C为圆心,以大于的长为半径画弧,两弧交于点E,F,直线交于点M,交于点N,若 , , 则边的长为( )
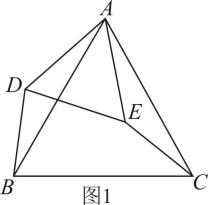
A、 B、 C、 D、8. 某厂家今年一月份的口罩产量是30万个,三月份的口罩产量是50万个,若设该厂家一月份到三月份的口罩产量的月平均增长率为x.则所列方程为( )A、30(1+x)2=50 B、30(1﹣x)2=50 C、30(1+x2)=50 D、30(1﹣x2)=509. 如图,是矩形的对角线,分别以点A,C为圆心,以大于的长为半径画弧,两弧交于点E,F,直线交于点M,交于点N,若 , , 则边的长为( )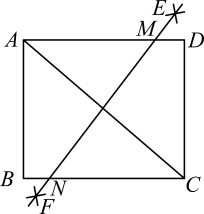 A、6 B、10 C、 D、10. 如图,已知菱形的边长为4,对角线相交于点O,点分别是边上的动点, , 连接 , 与相交于点E.以下四个结论:①点是等边三角形;②的最小值是;③若时,;④当时, . 其中正确的个数有( )
A、6 B、10 C、 D、10. 如图,已知菱形的边长为4,对角线相交于点O,点分别是边上的动点, , 连接 , 与相交于点E.以下四个结论:①点是等边三角形;②的最小值是;③若时,;④当时, . 其中正确的个数有( )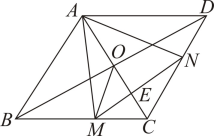 A、1个 B、2个 C、3个 D、4
A、1个 B、2个 C、3个 D、4二、填空题
-
11. 关于x的一元二次方程的一个根是2,则a的值是;12. 四条线股a、b、c、d成比例,其中cm,cm,cm,则b的长为 .13. 在一个不透明的盒子里装有5个黑色棋子和若干白色棋子,每个棋子除颜色外都相同,任意摸出一个棋子,记下颜色后再放回盒子,通过大量重复摸棋实验后发现,摸到黑色棋子的频率稳定在20%,估计白色棋子的个数为;14. 如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
 15. 如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方,某一时刻,太阳光线恰好垂直照射叶片、 , 此时各叶片影子在点M右侧成线段 . 测得 , , 垂直于地面的木棒与影子的比为 . 则点O、M之间的距离等于m;
15. 如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方,某一时刻,太阳光线恰好垂直照射叶片、 , 此时各叶片影子在点M右侧成线段 . 测得 , , 垂直于地面的木棒与影子的比为 . 则点O、M之间的距离等于m; 16. 如图,是边长为1的等边三角形,分别取边的中点D、E,连接 , 作得到四边形 , 它的周长记作;分别取的中点 , 连接 , 作 , 得到四边形 , 它的周长记作 , …,照此规律作下去,则等于 .
16. 如图,是边长为1的等边三角形,分别取边的中点D、E,连接 , 作得到四边形 , 它的周长记作;分别取的中点 , 连接 , 作 , 得到四边形 , 它的周长记作 , …,照此规律作下去,则等于 .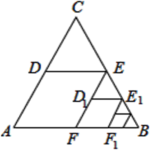
三、解答题
-
17. 解方程:18. 若 , 且 , 求的值是多少?19. 如图,是正方形的对角线上的两点,且 , 求证:;
 20. 如图,在中,D、E分别是边、上的点,连接 , 且 , , , , 求的长.
20. 如图,在中,D、E分别是边、上的点,连接 , 且 , , , , 求的长.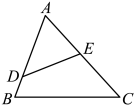 21. 如图,一路灯与墙相距20米,当身高米的小亮在离墙17米的D处时,影长为1米.
21. 如图,一路灯与墙相距20米,当身高米的小亮在离墙17米的D处时,影长为1米. (1)、求路灯B的高度;(2)、若点P为路灯,请画出小亮位于N处时,在路灯P下的影子NF(用粗线段表示出来)22. 如图,用一段长为的篱笆围成一个一边靠墙的矩形围栏(墙长),若这个围栏的面积为 , 求与墙垂直的一边的长度.
(1)、求路灯B的高度;(2)、若点P为路灯,请画出小亮位于N处时,在路灯P下的影子NF(用粗线段表示出来)22. 如图,用一段长为的篱笆围成一个一边靠墙的矩形围栏(墙长),若这个围栏的面积为 , 求与墙垂直的一边的长度. 23. 如图,在平面直角坐标系中,的三个顶点的坐标分别为 , , .
23. 如图,在平面直角坐标系中,的三个顶点的坐标分别为 , , .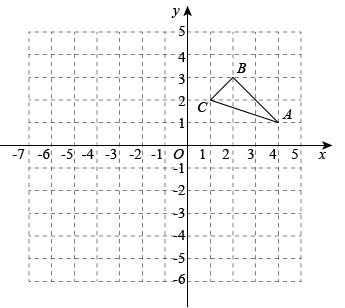 (1)、画出先向下平移1个单位长度,再向左平移2个单位长度的 , 并写出点的坐标;(2)、以原点O为位似中心,在所给的方格纸纸中(不能超出方格纸)画一个 , 使它与的相似比为 , 并写出点的坐标;(3)、在内有一点 , 按(1)与(2)的方式得到的对应点的坐标是 .24. 为喜迎中国共产党第二十次全国代表大会的召开,某中学举行党史知识竞赛.团委随机抽取了部分学生的成绩作为样本,把成绩按达标,良好,优秀,优异四个等级分别进行统计,并将所得数据绘制成如下不完整的统计图.
(1)、画出先向下平移1个单位长度,再向左平移2个单位长度的 , 并写出点的坐标;(2)、以原点O为位似中心,在所给的方格纸纸中(不能超出方格纸)画一个 , 使它与的相似比为 , 并写出点的坐标;(3)、在内有一点 , 按(1)与(2)的方式得到的对应点的坐标是 .24. 为喜迎中国共产党第二十次全国代表大会的召开,某中学举行党史知识竞赛.团委随机抽取了部分学生的成绩作为样本,把成绩按达标,良好,优秀,优异四个等级分别进行统计,并将所得数据绘制成如下不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)、本次调查的学生数是人,圆心角β=度;(2)、补全条形统计图;(3)、已知该中学共有1500名学生,估计此次竞赛该校获优异等级的学生人数为多少?(4)、若在这次竞赛中有A、B、C、D四人成绩均为满分,现从中抽取2人代表学校参加区级比赛,请用列表或画树状图的方法求出恰好抽到A、C两人同时参赛的概率.