辽宁省沈阳市沈北新区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-11-10 类型:期中考试
一、单选题
-
1. 利用配方法解方程x2+2x=1时,方程可变形为( )A、(x+1)2=2 B、(x﹣1)2=2 C、(x+1)2=0 D、(x﹣1)2=02. 方程的根是( )A、 B、 C、 D、3. 如图,已知四边形的对角线相交于O,则下列条件能判断它是正方形的的是( )
 A、 , B、 C、 , , D、 ,4. 关于x的一元二次方程没有实数根,则m的值可能是( )A、-2 B、0 C、3 D、55. 如图,在菱形中,对角线、交于点 , 已知 , , 则菱形的面积是( )
A、 , B、 C、 , , D、 ,4. 关于x的一元二次方程没有实数根,则m的值可能是( )A、-2 B、0 C、3 D、55. 如图,在菱形中,对角线、交于点 , 已知 , , 则菱形的面积是( ) A、4 B、8 C、16 D、206. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,则CD的长为( )
A、4 B、8 C、16 D、206. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,则CD的长为( ) A、5 B、6 C、7 D、87. 如图,△ABC与△DEF是位似图形,位似比为2:3,已知AB=4,则DE的长等于( )
A、5 B、6 C、7 D、87. 如图,△ABC与△DEF是位似图形,位似比为2:3,已知AB=4,则DE的长等于( ) A、6 B、5 C、9 D、8. 九年级1907班文学小组在举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了132本图书,如果设全组共有名同学,依题意,可列出的方程是( )A、 B、 C、 D、9. 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
A、6 B、5 C、9 D、8. 九年级1907班文学小组在举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了132本图书,如果设全组共有名同学,依题意,可列出的方程是( )A、 B、 C、 D、9. 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )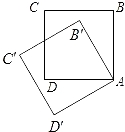 A、1﹣ B、1﹣ C、 D、10. 菱形ABCD的一条对角线的长为6,边AB的长是方程 的一个根,则菱形ABCD的周长为( )A、16 B、12 C、12或16 D、无法确定
A、1﹣ B、1﹣ C、 D、10. 菱形ABCD的一条对角线的长为6,边AB的长是方程 的一个根,则菱形ABCD的周长为( )A、16 B、12 C、12或16 D、无法确定二、填空题
-
11. 把1m的线段进行黄金分割,则分成较短的线段长为 .12. 如图,在△ABC中,点D,E分别在AB,AC上,且DE∥BC.若AD=2,AB=3,DE=4,则BC的长为 .
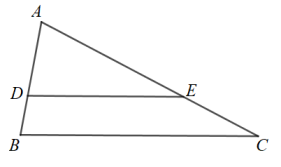 13. 若 , , 则a的值为 .14. 如图,在Rt 中, 于 ,若 ,则 .
13. 若 , , 则a的值为 .14. 如图,在Rt 中, 于 ,若 ,则 . 15. 如图,在中, , , , 动点从点出发,沿方向运动,动点从点出发,沿方向运动,如果点 , 同时出发, , 的运动速度均为 . 那么运动 秒时,它们相距 .
15. 如图,在中, , , , 动点从点出发,沿方向运动,动点从点出发,沿方向运动,如果点 , 同时出发, , 的运动速度均为 . 那么运动 秒时,它们相距 . 16. 如图,在 中, ,且 , ,点 是斜边 上的一个动点,过点 分别作 于点 , 于点 ,连接 ,则线段 的最小值为 .
16. 如图,在 中, ,且 , ,点 是斜边 上的一个动点,过点 分别作 于点 , 于点 ,连接 ,则线段 的最小值为 .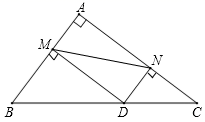
三、解答题
-
17. 用适当的方法解一元二次方程(1)、;(2)、 .18. 如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.
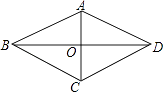 (1)、求证:四边形ABCD是菱形;(2)、若CD=3,BD=2 ,求四边形ABCD的面积.19. 如图,在△ABC中,∠C=90°,AC=6cm,BC=8m,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止运动.
(1)、求证:四边形ABCD是菱形;(2)、若CD=3,BD=2 ,求四边形ABCD的面积.19. 如图,在△ABC中,∠C=90°,AC=6cm,BC=8m,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止运动. (1)、如果点P,Q同时出发,经过几秒钟时△PCQ的面积为8cm2?(2)、如果点P,Q同时出发,经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似?20. 某地的2020年公共事业投入经费40000万元,其中教育经费占15%,2022年教育经费实际投入7260万元,若该县这两年教育经费的年平均增长率相同.(1)、求该地这两年教育经费平均增长率;(2)、若该地这两年教育经费平均增长率保持不变,那么2023年教育经费会达到8000万元吗?21. 某商场销售一批名牌衬衫,每件进价为100元,若每件售价为160元,则平均每个月可售出100件,经调查发现,每件衬衫每降价2元,商场平均每月可多售出10件,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,设每件衬衫降价x元.(1)、用含x的代数式表示每月可售出的衬衫件数为;(2)、若商场每月要盈利7875元,请你帮助商场算一算,每件衬衫应降价多少元?22. 在菱形ABCD中,过点B作于点E,点F在边AB上,AF=CE,连接BD、DF.
(1)、如果点P,Q同时出发,经过几秒钟时△PCQ的面积为8cm2?(2)、如果点P,Q同时出发,经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似?20. 某地的2020年公共事业投入经费40000万元,其中教育经费占15%,2022年教育经费实际投入7260万元,若该县这两年教育经费的年平均增长率相同.(1)、求该地这两年教育经费平均增长率;(2)、若该地这两年教育经费平均增长率保持不变,那么2023年教育经费会达到8000万元吗?21. 某商场销售一批名牌衬衫,每件进价为100元,若每件售价为160元,则平均每个月可售出100件,经调查发现,每件衬衫每降价2元,商场平均每月可多售出10件,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,设每件衬衫降价x元.(1)、用含x的代数式表示每月可售出的衬衫件数为;(2)、若商场每月要盈利7875元,请你帮助商场算一算,每件衬衫应降价多少元?22. 在菱形ABCD中,过点B作于点E,点F在边AB上,AF=CE,连接BD、DF.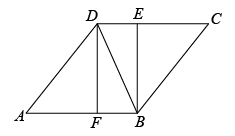 (1)、求证:四边形BFDE是矩形;(2)、若BD=2 , BE=4,求BC的长.23. 如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)、求证:四边形BFDE是矩形;(2)、若BD=2 , BE=4,求BC的长.23. 如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
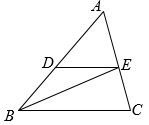 (1)、求证:AE•BC=BD•AC;(2)、如果 =3, =2,DE=6,求BC的长.24. 如图①,P是菱形对角线上的一点,点在的延长线上,且 .
(1)、求证:AE•BC=BD•AC;(2)、如果 =3, =2,DE=6,求BC的长.24. 如图①,P是菱形对角线上的一点,点在的延长线上,且 . (1)、求证:;(2)、求证:;(3)、如图②,当四边形为正方形时,连接 , 试探究线段与线段的数量关系,并说明理由.25. 在 , , .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)、求证:;(2)、求证:;(3)、如图②,当四边形为正方形时,连接 , 试探究线段与线段的数量关系,并说明理由.25. 在 , , .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.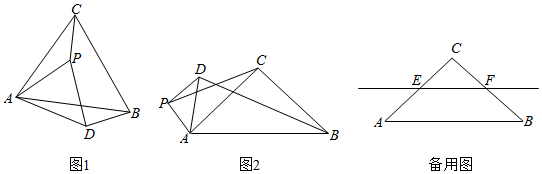 (1)、观察猜想
(1)、观察猜想如图1,当 时, 的值是 , 直线BD与直线CP相交所成的较小角的度数是.
(2)、类比探究如图2,当 时,请写出 的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)、解决问题当 时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时 的值.