江西省景德镇市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-10 类型:期末考试
一、单选题
-
1. 下列四个数中,最小的数是( )A、-3 B、 C、 D、2. 下列各图经过折叠后不能围成一个正方体的是( )A、
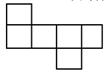 B、
B、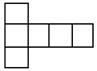 C、
C、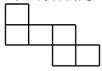 D、
D、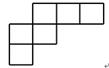 3. 初中生骑电动车上学存在安全隐患,为了解某初中2400个学生家长对“中学生骑电动车上学”的态度,从中随机调查200个家长,结果有180个家长持反对态度,则下列说法正确的是( )A、调查方式是普查 B、该校只有180个家长持反对态度 C、样本是200个家长 D、该校约有90%的家长持反对态度4. 用长的铝合金做成一个长方形的窗框(如图,单位:),设长方形窗框的横条长度为 , 则长方形窗框的面积为( )
3. 初中生骑电动车上学存在安全隐患,为了解某初中2400个学生家长对“中学生骑电动车上学”的态度,从中随机调查200个家长,结果有180个家长持反对态度,则下列说法正确的是( )A、调查方式是普查 B、该校只有180个家长持反对态度 C、样本是200个家长 D、该校约有90%的家长持反对态度4. 用长的铝合金做成一个长方形的窗框(如图,单位:),设长方形窗框的横条长度为 , 则长方形窗框的面积为( ) A、 B、 C、 D、5. 《孙子算经》中有个问题,原文:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价几何?”这道题的意思是:今有若干人共同买羊,如果每人出5枚钱,则相差45枚钱;如果每人出7枚钱,则仍然相差3枚钱,求买羊人数和羊价?设有买羊人数为人,则可列方程为( )A、 B、 C、 D、6. 将一张长方形纸片ABCD按如图所示的方式折叠,AE、AF为折痕,点B、D折叠后的对应点分别为、 , 若=10°,则∠EAF的度数为( )
A、 B、 C、 D、5. 《孙子算经》中有个问题,原文:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价几何?”这道题的意思是:今有若干人共同买羊,如果每人出5枚钱,则相差45枚钱;如果每人出7枚钱,则仍然相差3枚钱,求买羊人数和羊价?设有买羊人数为人,则可列方程为( )A、 B、 C、 D、6. 将一张长方形纸片ABCD按如图所示的方式折叠,AE、AF为折痕,点B、D折叠后的对应点分别为、 , 若=10°,则∠EAF的度数为( ) A、40° B、45° C、50° D、55°
A、40° B、45° C、50° D、55°二、填空题
-
7. 已知 , 则 .8. 已知数轴上有一点表示的数是 , 将点向右移动4个单位至点 , 则点表示的数是 .9. 某校为鼓励学生课外阅读,制定了“阅读奖励方案”.方案公布后,随机征求了100名学生的意见,并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计,绘制成如图所示的扇形统计图.若该校有1000名学生,则赞成该方案的学生约有人.
 10. 的方向是北偏东14°,的方向是北偏东69°,若平分 , 则的方向是 .
10. 的方向是北偏东14°,的方向是北偏东69°,若平分 , 则的方向是 . 11. 若是关于的方程的解,则关于的方程的解为 .12. 一副三角板如图放置,将三角板绕点逆时针旋转 , 使得三角板的任意一边所在的直线与的一边垂直,则的度数为 .
11. 若是关于的方程的解,则关于的方程的解为 .12. 一副三角板如图放置,将三角板绕点逆时针旋转 , 使得三角板的任意一边所在的直线与的一边垂直,则的度数为 .
三、解答题
-
13.(1)、解方程:(2)、计算:14. 当为何值时,代数式与的和等于3?15. 已知一直棱柱共有11个面,且它的底面边长都相等,侧棱长是10厘米,侧面积是180平方厘米.(1)、它是几棱柱?(2)、它的底面边长是多少?16. 已知 , 求的值.17. 郝先生一家在1月1号从景德镇驾车去南昌“奥特莱斯”百货商城购物,郝先生在高速上开了2个小时,下了高速之后又在城区开了36分钟,且高速上的平均车速是下高速之后城区平均车速的2倍,已知出发地与目的地的路程大约为253千米,试求出高速上以及城区里的平均车速?18. 为了解景德镇市民对“双减政策”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“ . 非常了解”、“ . 了解”、“ . 基本了解”、“ . 不太了解”四个等级进行统计,并将统计结果绘制成了如下两幅不完整的统计图(图1、图2),请根据图中的信息解答下列问题.
 (1)、这次调查的市民人数为人,图2中,n= .(2)、补全图1中的条形统计图;(3)、在图2中的扇形统计图中,表示“ . 基本了解”所在扇形的圆心角度数为度;(4)、据统计,2021年景德镇市约有市民200万人,那么根据抽样调查的结果,可估计对“双减政策”的知晓程度为“ . 非常了解”的市民约有万人.19. 某剧院座位的一部分为扇形状,座位数按下列方式设置:
(1)、这次调查的市民人数为人,图2中,n= .(2)、补全图1中的条形统计图;(3)、在图2中的扇形统计图中,表示“ . 基本了解”所在扇形的圆心角度数为度;(4)、据统计,2021年景德镇市约有市民200万人,那么根据抽样调查的结果,可估计对“双减政策”的知晓程度为“ . 非常了解”的市民约有万人.19. 某剧院座位的一部分为扇形状,座位数按下列方式设置:排数
1
2
3
4
5
6
…
座位数
50
53
56
59
____
____
…
按这种方式排下去
(1)、第5、6排各有多少个座位?完成上表填空;(2)、第n排有多少个座位?(3)、在(2)的代数式中,第17排有多少个座位?20. 如图,已知 , 是的平分线,是的平分线. (1)、求的度数;(2)、若 , 求的度数.21. 教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米):+5,﹣4,﹣8,+10,+3,﹣6,+7,﹣11.(1)、将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?(2)、若汽车耗油量为0.2升/千米,则当天耗油多少升?若汽油价格为5.70元/升,则小王共花费了多少元钱?22. A、B两地分别有水泥20吨和30吨,C、D两地分别需要水泥15吨和35吨;已知从A、B到C、D的运价如下表:
(1)、求的度数;(2)、若 , 求的度数.21. 教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米):+5,﹣4,﹣8,+10,+3,﹣6,+7,﹣11.(1)、将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?(2)、若汽车耗油量为0.2升/千米,则当天耗油多少升?若汽油价格为5.70元/升,则小王共花费了多少元钱?22. A、B两地分别有水泥20吨和30吨,C、D两地分别需要水泥15吨和35吨;已知从A、B到C、D的运价如下表:到C地
到D地
A地
每吨15元
每吨12元
B地
每吨10元
每吨9元
(1)、若从A地运到C地的水泥为x吨,则用含x的式子表示从A地运到D地的水泥吨,从A地将水泥运到D地的运输费用为元.(2)、用含x的代数式表示从A、B两地运到C、D两地的总运输费,并化简该式子.(3)、当总费用为545元时水泥该如何运输调配?23. 已知直线上有一点 , 点 , 同时从出发,在直线上分别向左,向右作匀速运动,且 , 的速度比为 , 设运动时间为 . (该数轴单位长度为) (1)、当 , . 此时,
(1)、当 , . 此时,①点的速度是 ▲ ;点的速度是 ▲ ;
②若点为直线上一点,且 , 求的值.
(2)、在(1)的条件下,若 , 同时按原速向左运动,再经过几秒,有?