内蒙古自治区兴安盟乌兰浩特市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-10 类型:期末考试
一、单选题
-
1. 下列各对数中,运算后结果相等的是( )A、23和32 B、(-2)3与-23 C、(-3)2与-32 D、与()²2. 在数轴上与点-3的距离等于4的点表示的数是( )A、1 B、1或-7 C、-7 D、-1或73. 地球绕太阳公转的轨道半径约是149000000千米,用科学记数法表示这个数为( )A、149×106 B、1.49×108 C、0.149×109 D、1.49×1094. 下列语句中正确的是( )A、单项式2mn2的次数是2 B、-x2的系数是1 C、是单项式 D、2x2y+3xy-4是三次三项式5. 在代数式4xy, , , 中,整式的个数是( )A、3个 B、2个 C、1个 D、0个6. 下列式子中,是一元一次方程的是( )A、x+4>2 B、 C、x-3=y+5 D、7. 根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )A、
 B、
B、 C、
C、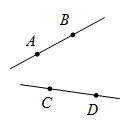 D、
D、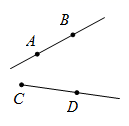 8. 今年父亲的年龄是儿子的5倍,5年前父亲的年龄是儿子的15倍,设今年儿子的年龄为x,可得方程( )A、5x-5=15(x-5) B、5x+5=15(x-5) C、5x-5=15(x+5) D、5x+5=15(x+5)9. 防控疫情必须勤洗手、戴口罩,讲究个人卫生.如图是一个正方体展开图,现将其围成一个正方体后,则与“手”相对的是( )
8. 今年父亲的年龄是儿子的5倍,5年前父亲的年龄是儿子的15倍,设今年儿子的年龄为x,可得方程( )A、5x-5=15(x-5) B、5x+5=15(x-5) C、5x-5=15(x+5) D、5x+5=15(x+5)9. 防控疫情必须勤洗手、戴口罩,讲究个人卫生.如图是一个正方体展开图,现将其围成一个正方体后,则与“手”相对的是( )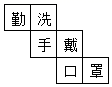 A、勤 B、口 C、戴 D、罩10. 如图, 为北偏东方向, , 则的方向为( )
A、勤 B、口 C、戴 D、罩10. 如图, 为北偏东方向, , 则的方向为( ) A、南偏东 B、南偏东 C、南偏西 D、北偏东11. 钟表盘上指示的时间是11时20分,此刻时针与分针之间的夹角为( )A、 B、 C、 D、12. 济青高铁北线,共设有11个不同站点,要保证每两个站点之间都有高铁可乘,需要印制不同的火车票( )A、110种 B、132种 C、55种 D、66种
A、南偏东 B、南偏东 C、南偏西 D、北偏东11. 钟表盘上指示的时间是11时20分,此刻时针与分针之间的夹角为( )A、 B、 C、 D、12. 济青高铁北线,共设有11个不同站点,要保证每两个站点之间都有高铁可乘,需要印制不同的火车票( )A、110种 B、132种 C、55种 D、66种二、填空题
-
13. 小丽妈妈买了5斤水果,第一天吃了 , 则还剩下斤.14. 如果a、b互为倒数,c、d互为相反数,且m=1,则代数式2ab-(c+d)+m2= .15. 已知a-b=4,则3a-3b-5的值为 .16. 如图是一所建筑住宅的平面图(图中长度单位:m),用式子表示这块住宅的建筑面积为 m2 .
 17. 某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本40元;按原价的九折出售,那么每件盈利20元,则这种衬衫的原价是元.
17. 某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本40元;按原价的九折出售,那么每件盈利20元,则这种衬衫的原价是元.三、解答题
-
18. 计算(1)、-12021-(1-0.5)[3-(-3)3];(2)、-52-[(-2)3+(1-8)÷(-2)].19. 解方程:(1)、2-3x=5x+7;(2)、x6 .20. 先化简,再求值(1)、(3x2−3)−2( )其中(2)、 ,其中x=-1,y=121.(1)、在下面带有箭头的直线上先确定好原点以及单位长度,然后在所得的数轴上把下列各数表示出来:-2,3.5, , 2.75, , -3.
 (2)、将上面6个数用“<”连接为: .22. 若方程3(2x-2)=2-3x的解与关于x的方程6-2k=2(x+3)的解相同,求k的值.23. 列方程,解应用题:
(2)、将上面6个数用“<”连接为: .22. 若方程3(2x-2)=2-3x的解与关于x的方程6-2k=2(x+3)的解相同,求k的值.23. 列方程,解应用题:新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品.某公司购进一批口罩供员工使用,若每人发50个口罩,则剩余80个口罩;若每人发55个口罩,则还缺35个口罩.这个公司有多少名员工?
24. 某检修小组乘汽车自A地出发,检修南北走向的供电线路.南记为正,北记为负.一天所走路程(单位:千米)为:-10,-3,+4,-2,-8,+16,-2,+12,+8,-5;问:(1)、最后他们是否回到出发点A?若没有,则在A地的什么方向?距离A地多远?(2)、若每千米耗油0.08升,则今天共耗油多少升?25. 如图,O是直线AB上点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC. (1)、若∠BOC=70°,求∠COD和∠EOC的度数;(2)、写出∠COD与∠EOC具有的数量关系,并说明理由.26. 如图,已知数轴上原点为O,点B表示的数为-3,A在B的右边,且A与B的距离是10.动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,同时动点Q从点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)、若∠BOC=70°,求∠COD和∠EOC的度数;(2)、写出∠COD与∠EOC具有的数量关系,并说明理由.26. 如图,已知数轴上原点为O,点B表示的数为-3,A在B的右边,且A与B的距离是10.动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,同时动点Q从点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒. (1)、点A表示的数是 , 点P表示的数是(用含t的代数式表示),点Q表示的数是(用含t的代数式表示);(2)、是否存在某一时刻t,使点P与点Q到点O的距离相等?若存在,求出t的值;若不存在,请说明理由;(3)、当t为何值时,点P与点Q之间的距离为5?
(1)、点A表示的数是 , 点P表示的数是(用含t的代数式表示),点Q表示的数是(用含t的代数式表示);(2)、是否存在某一时刻t,使点P与点Q到点O的距离相等?若存在,求出t的值;若不存在,请说明理由;(3)、当t为何值时,点P与点Q之间的距离为5?