内蒙古自治区赤峰市松山区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. 赤峰地区冬季某日最高气温 $- 3^{°} C$ ，最低 $- 2 4^{°} C$ ，则最高气温比最低气温高（）

A、 $- 2 7^{°} C$ B、 $- 2 1^{°} C$ C、 $2 7^{°} C$ D、 $2 1^{°} C$

查看试题解析
2. 据报道，目前我国“天河二号”超级计算机的运算速度位居全球第一，其运算速度达到了每秒338 600 000亿次，数字338 600 000用科学记数法可简洁表示为（　　）

A、3.386×10⁸ B、0.3386×10⁹ C、33.86×10⁷ D、3.386×10⁹

查看试题解析
3. 如图可知， $∠ M O N$ 的大小可由量角器测得，则 $∠ M O N$ 的余角的补角大小为（）

A、 $20 °$ B、 $70 °$ C、 $110 °$ D、 $160 °$

查看试题解析
4. 已知多项式 $2 x^{2} - 4 y$ 的值是 $- 2$ ，则多项式 $x^{2} + 6 - 2 y$ 的值是（）

A、4 B、5 C、-4 D、8

查看试题解析
5. 下列说法：①对顶角相等：②相等的角是对顶角；③等角的余角相等；④如果两个角的和等于 $180 °$ ，那么这两个角互为补角；其中正确的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 如图是一个正方体的表面展开图，则原正方体中与“的”字所在的面相对的面上标的汉字是（）

A、祖 B、国 C、伟 D、大

查看试题解析
7. 如图所示，直线AB，CD相交于点O，“阿基米德曲线”从点O开始生成，如果将该曲线与每条射线的交点依次标记为2，-4，6，-8，10，-12，…．那么标记为“2022”的点在（）

A、射线OA上 B、射线OB上 C、射线OC上 D、射线OD上

查看试题解析
8. 下列结论错误的是（）

A、若a=b，则 $\frac{a}{m^{2} + 2} = \frac{b}{m^{2} + 2}$ B、若 $\frac{a}{m - 1} = \frac{b}{m - 1}$ ，则a=b C、若x=3，则x²=3x D、若ax+2=bx+2，则a=b

查看试题解析
9. 如图，测量运动员跳远成绩选取的是AB的长度，其依据是（）

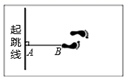A、两点确定一条直线 B、垂线段最短 C、两点之间线段最短 D、两点之间直线最短

查看试题解析
10. 已知：如图，直线 $B O ⊥ A O$ 于点O，OB平分 $∠ C O D ， ∠ A O C = 68 °$ ，则 $∠ D O A$ 的度数是（）

A、 $90 °$ B、 $118 °$ C、 $112 °$ D、 $120 °$

查看试题解析
11. 学校组织学生参加知识问答，问答活动共设有20道选择题，各题分值相同，每题必答，如表记录了A、B、C三名学生的得分情况，按此规则，参赛学生D的得分可能是（）．
参赛学生
答对题数
答错题数
得分
A
20
0
100
B
19
1
93
C
15
5
65

A、75 B、63 C、56 D、44

查看试题解析
12. 如图，长方形 $A B C D$ 沿直线 $E F$ 、 $E G$ 折叠后，点A和点D分别落在直线l上的点 $A^{'}$ 和点 $D^{'}$ 处，若 $∠ 1 = 30 °$ ，则 $∠ 2$ 的度数为（）

A、30° B、60° C、50° D、55°

查看试题解析
13. 整理一批图书，由一个人做要30小时完成，现计划由一部分人先做3小时，然后增加2人与他们一起做6小时，完成这项工作，假设这些人的工作效率相同，具体应先安排多少人工作？如果设安排x人先做3小时，下列四个方程中正确的是（）

A、 $\frac{3 x}{30} + \frac{6 (x + 2)}{30} = 1$ B、 $\frac{3 (x + 2)}{30} + \frac{6 x}{30} = 1$ C、 $\frac{3 x}{30} + \frac{6 (x - 2)}{30} = 1$ D、 $\frac{3 x}{30} + \frac{6 x}{30} = 1$

查看试题解析
14. 如图，点M是AB的中点，点N是BD的中点， $A B = 8 c m ， B C = 12 c m ， C D = 6 c m$ ．则MN的长为（）

A、7cm B、10cm C、13cm D、16cm

查看试题解析

二、填空题

15. 如图是某同学家里楼房平面图（长度单位：m），用含有a的代数式表示该住宅的建筑面积是 $m^{2}$ ．

查看试题解析
16. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有人共买鸡，人出九，盈十一；人出六，不足十六．问人数几何？”
译文：“有几个人共同出钱买鸡，如果每人出九钱，那么多了十一钱；如果每人出六钱，那么少了十六钱．问：有几个人共同出钱买鸡？

设有x个人共同买鸡，根据题意列一元一次方程．

查看试题解析
17. 某个体商贩在一次买卖中，同时卖出两件上衣，每件都以135元出售，若按成本计算，其中一件盈利 $25 %$ ，另一件亏本 $25 %$ ，则在这次买卖中，他赔了元．

查看试题解析
18. 如图是某同学在沙滩上用石子摆成的小房子，第n个图形需要颗石子，

查看试题解析

三、解答题

19. 计算：

(1)、 $(- 4)^{2} - 9 \div \frac{3}{4} + (- 2) \times (- 1) + (- \frac{1}{2})$

(2)、先化简，再求值： $6 y^{3} + 4 (x^{3} - 2 x y) - 2 (3 y^{3} - x y)$ ，其中 $x = - 2 ， y = 3$ ．

查看试题解析
20. 解方程：

(1)、 $4 x + 3 = 2 (x - 1) + 1$ ；

(2)、 $\frac{2 x - 1}{3} = \frac{3 x - 5}{4} + 1$ ．

查看试题解析
21. 如图，已知点A、B、O、M，请按下列要求作图并解答．
⑴连接 $A B$ ；
⑵画射线 $O M$ ；
⑶在射线 $O M$ 上取点C，使得 $O C = 2 A B$ （尺规作图，保留作图痕迹）；
⑷在图中确定一点P，使点P到A、B、O、C四个点的距离和最短，请写出作图依据．

查看试题解析
22. 某市为鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过40立方米时，按2元/立方米计费；月用水量超过40立方米时，其中的40立方米仍按2元/立方米收费，超过部分按3.5元/立方米计费.设每户家庭月用水量为x立方米.

(1)、当x不超过40时，应收水费为（用x的代数式表示）；当x超过40时，应收水费为（用x的代数式表示化简后的结果）；

(2)、小明家四月份用水26立方米，五月份用水52立方米，请帮小明计算一下他家这两个月一共应交多少元水费？

(3)、小明家六月份交水费150元，请帮小明计算一下他家这个月用水量多少立方米？

查看试题解析

23. 暑假里某班同学相约一起去某公园划船，在售票处了解到该公园划船项目收费标准如下：

船型	两人船（仅限两人）	四人船（仅限四人）	六人船（仅限六人）	八人船（仅限八人）
每船租金（元/小时）		100	130

(1)、其中，两人船项目和八人船项目单价模糊不清，通过询问，了解到以下信息：

①一只八人船每小时的租金比一只两人船每小时的租金的2倍少30元；

②租2只两人船，3只八人船，游玩一个小时，共需花费630元．

请根据以上信息，求出两人船项目和八人船项目每小时的租金；

(2)、若该班本次共有18名同学一起来游玩，每人乘船的时间均为1小时，且每只船均坐满，试列举出可行的方案（至少四种），通过观察和比较，找到所有方案中最省钱的方案．

查看试题解析

24. 阅读材料，解决问题

(1)、我们学习了乘方的定义和意义，根据乘方和乘法两种运算之间的转化了解到：
$2^{3} = 2 \times 2 \times 2$ ； $2^{4} = 2 \times 2 \times 2 \times 2$ ；
观察上述算式，
$2^{3} \times 2^{4} = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^{7}$ ；
可以得到： $2^{3} \times 2^{4} = 2^{7}$ ；
类比上述式子，你能够得到：
$1 0^{3} \times 1 0^{5} =$ ；

(2)、 $a^{2} \times a^{3} =$ ；

(3)、利用由特殊到一般的思想，可以得到：
$a^{m} \cdot a^{n} =$ （m、n都是正整数）

(4)、我们把类似于 $a^{m}$ 和 $a^{n}$ 这样的式子叫同底数幂；因此可以得到“同底数幂的乘法”法则：
“同底数幂相乘，底数不变，指数相加”
知识运用：
$x^{3} \cdot x =$ ；

(5)、 $y^{n} \cdot y^{n + 1}$ ．

(6)、已知 $x^{a} = 8 ， x^{b} = 9$ ，则 $x^{a + b}$ 的值是．

查看试题解析
25. 点O是直线AB上的一点，射线OC从OA出发绕点O顺时针方向旋转，旋转到OB停止，设 $∠ A O C = α$ （ $0 ° \leq α \leq 180 °$ ），射线 $O D ⊥ O C$ ，作射线OE平分 $∠ B O D$ ．

(1)、如图1，若 $α = 40 °$ ，且OD在直线AB的上方，求 $∠ D O E$ 的度数（要求写出简单的几何推理过程）．

(2)、射线OC顺时针旋转一定的角度得到图2，当射线OD在直线AB的下方时，其他条件不变，请你用含 $α$ 的代数式表示 $∠ D O E$ 的度数，（要求写出简单的几何推理过程）．

(3)、射线OC从OA出发绕点O顺时针方向旋转到OB，在旋转过程中你发现 $∠ D O E$ 与 $∠ A O C$ （ $0 ° \leq ∠ A O C \leq 180 ° ， 0 ° \leq ∠ D O B \leq 180 °$ ）之间有怎样的数量关系？请你直接用含 $α$ 的代数式表示 $∠ D O E$ 的度数．

查看试题解析
26. 点A、B在数轴上对应的数分别为a、b，且a、b满足 $| a + 1 | + {| b - 3 |}^{2} = 0$ ．

(1)、如图1，求线段AB的长；

(2)、若点C在数轴上对应的数为x，且x是方程 $2 x + 1 = \frac{1}{2} x - 2$ 的根，在数轴上是否存在点P使 $P A + P B = B C$ ，若存在，求出点P对应的数，若不存在，说明理由；

(3)、如图2，点P在B点右侧，PA的中点为M，N为PB靠近于B点的四等分点，当P在B的右侧运动时，有两个结论：① $P M - 2 B N$ 的值不变；② $P M - \frac{2}{3} B N$ 的值不变，其中只有一个结论符合题意，请判断正确的结论，并直接写出该值．

查看试题解析

参赛学生	答对题数	答错题数	得分
A	20	0	100
B	19	1	93
C	15	5	65