内蒙古自治区赤峰市阿鲁科尔沁旗2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. -2022的相反数是（）

A、 $- \frac{1}{2022}$ B、 $\frac{1}{2022}$ C、-2022 D、2022

查看试题解析
2. 赤峰市是内蒙古自治区的9个地级市之一，位于内蒙古自治区东南部，蒙冀辽三省区交汇处，全市总土地面积约为90021平方千米将90021用科学记数法表示为（）

A、 $90021 \times 1 0^{2}$ B、 $9.0021 \times 1 0^{5}$ C、 $9.0021 \times 1 0^{4}$ D、 $9.0021 \times 1 0^{3}$

查看试题解析
3. 如图，从直线EF外一点P向EF引四条线段PA，PB，PC，PD，其中最短的是（）

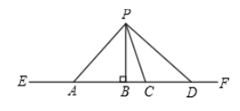A、PA B、PB C、PC D、PD

查看试题解析
4. 下列运算正确的是（）

A、 $3 a^{2} b - 2 b a^{2} = a^{2} b$ B、 $5 a - 4 b = a b$ C、 $a^{2} + a^{2} = a^{4}$ D、 $2 (a - 1) = 2 a - 1$

查看试题解析
5. 如图是从不同方向看某个立体图形得到的平面图形，这个立体图形的展开图可以是（）

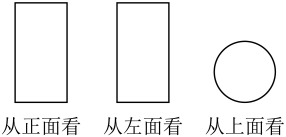A、 B、 C、 D、

查看试题解析
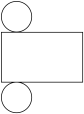6. 给出下列说法：① $\frac{2 x}{π}$ 的系数是2；② $\frac{x + y}{2}$ 是多项式；③ $x^{2} - x - 2$ 的常数项为2；④单项式 $x^{2} y$ 与 $2 x^{2} y$ 的和仍为单项式；⑤ $2 x - 5 x = 3 x + 1$ 是一元一次方程其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 实数a在数轴上的对应点的位置如图所示．若实数 $b$ 满足 $- a < b < a$ ，则b的值可以是（）

A、2 B、-1 C、-2 D、-3

查看试题解析
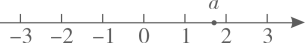8. 已知 $∠ A$ 与 $∠ B$ 互补， $∠ B$ 与 $∠ C$ 互余，若 $∠ A = 120 °$ ，则 $∠ C$ 的度数是（）

A、 $70 °$ B、 $60 °$ C、 $30 °$ D、 $20 °$

查看试题解析
9. 下列去括号正确的是（）

A、 $x - (5 y - 3 x) = x - 5 y - 3 x$ B、 $5 x - [2 y - (x - z)] = 5 x - 2 y + x - z$ C、 $2 x + (- 3 y + 7) = 2 x - 3 y - 7$ D、 $a - 3 (b - c + d) = a - 3 b - 3 c - 3 d$

查看试题解析
10. 下列等式的变形中，正确的是（）

A、如果 $s = \frac{1}{2} a b$ ，那么 $b = \frac{s}{2 a}$ B、如果 $x - 3 = y - 3$ ，那么 $x - y = 0$ C、如果 $m x = m y$ ，那么 $x = y$ D、如果 $x = 2 y + 1$ ，那么 $m x = 2 m y + 1$

查看试题解析
11. 如图，甲从A点出发向北偏东70°方向走到点B，乙从点A出发向南偏西15°方向走到点C，则∠BAC的度数是（）

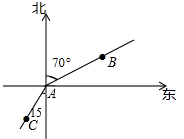A、85° B、105° C、125° D、160°

查看试题解析
12. 我国古代有很多经典的数学题，其中有一道题目是：良马日行二百里，驽马日行一百二十里，驽马先行十日，问良马几何追及之.意思是：跑得快的马每天走200里，跑得慢的马每天走120里，慢马先走10天，快马几天可追上慢马？若设快马 $x$ 天可追上慢马，则由题意可列方程为（）

A、 $120 + 10 x = 200 x$ B、 $120 x + 200 x = 120 \times 10$ C、 $200 x = 120 x + 200 \times 10$ D、 $200 x = 120 x + 120 \times 10$

查看试题解析
13. 按如图所示的运算程序，能使输出的结果为32的是（）

A、 $x = 2$ ， $y = 4$ B、 $x = 2$ ， $y = - 4$ C、 $x = 4$ ， $y = 2$ D、 $x = - 4$ ， $y = 2$

查看试题解析
14. 边长为1的正方形OABC从如图所示的位置（点O对应数0，点A对应数－1）开始在数轴上顺时针滚动（无滑动）．当正方形的某个顶点落在数2023在数轴上对应的点处时停止运动，此时落在数2023在数轴上对应点的这个顶点是（）

A、点A B、点B C、点C D、点O

查看试题解析

二、填空题

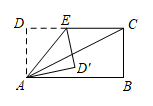
15. 计算：35°45′＋72°19′＝.

查看试题解析
16. 赤峰某日的最高气温是5℃，最低气温是－4℃，则该日最高气温比最低气温高℃．

查看试题解析
17. 方程2x＋a﹣4＝0的解是x＝﹣2，则a等于．

查看试题解析
18. 如图，把一长方形纸片ABCD的一角沿AE折叠，点D的对应点 $D ′$ 落在∠BAC内部．若 $∠ C A E = 2 ∠ B A D^{'}$ ，且 $∠ C A D^{'} = 15 °$ ，则∠DAE的度数为．

查看试题解析

三、解答题

19. 计算：

(1)、 $(\frac{1}{3} - \frac{5}{2} + \frac{1}{6}) \times (- 36)$ ；

(2)、 ${(- 1)}^{2022} \times 3 - 2^{3} + {(- \frac{1}{4})}^{2} \div | - \frac{1}{2^{5}} |$ ．

查看试题解析
20. 解方程：

(1)、4x+3＝2x+1；

(2)、 $\frac{x + 2}{4} - \frac{2 x - 3}{6}$ ＝1．

查看试题解析
21. 先化简，再求值： $2 (x^{2} y + x y^{2}) - 3 (x^{2} y - x) - 2 x y^{2} - 2 y$ ，其中x，y的值满足 $| x + 2 | + {(y - 2)}^{2} = 0$

查看试题解析
22. 我们把按一定规律排列的一列数称为数列．若对于一个数列中任意相邻有序的三个数a，b，c总满足 $c = a b + 2 a - b$ ，则称这个数列为“梦数列”．

(1)、若0，1，－1，2，y是“梦数列”，求y的值；

(2)、若数列…，x，3，6x－1，…是“梦数列”，求x的值．

查看试题解析
23. 近年来，我市香蕉产业不断做大做强，打造出“洛洛香”、“甜弯弯”等优质品业牌．如今又到了香蕉上市的季节，某商家以每箱60元的进价购入200箱香蕉，然后分批全部卖出．售价以每箱75元为标准，超过的部分记为正，低于的部分记为负，记录如下：
超出标准（单位：元）
+15
+12
+10
0
-8
-5
卖出数量（单位：箱）
50
20
40
30
30
30

(1)、求每箱香蕉的平均售价是多少元？

(2)、该商家卖完所有香蕉所获利润为多少元？

查看试题解析
24. 线段和角的计算．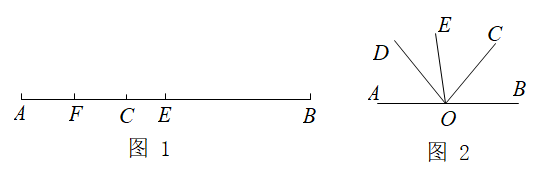

(1)、如图1，E是线段AB的中点，点C在线段AB上，F是AC的中点，若 $E F = 5 c m$ ， $A C = 6 c m$ ，求线段CE和AB的长．

(2)、如图2，已知O是直线AB上一点， $∠ A O E = ∠ C O D$ ，射线OC平分 $∠ B O E$ ，若 $∠ E O C = 50 °$ ．求∠DOE的度数．

查看试题解析
25. 如图是王阿姨刚接手的新房的地面平面结构图（图中长度单位：m），其中每间房屋地面都是长方形，她准备在客厅和卧室地面全部铺设复合地板，厨房和卫生间地面全部铺设瓷砖.根据图中数据解决以下问题：

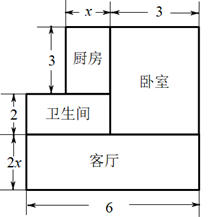(1)、求该房屋地面的总面积（用含x的式子表示）；

(2)、铺设完全部地面，有两个施工计费方案供王阿姨选择：
方案一：每平方米瓷砖的铺设费用为25元，每平方米复合地板的铺设费用为30元；

方案二：铺完全部地面，一口价1500元.

①当x为何值时，两种方案所花费用一样？

②若x=2，则王阿姨选择哪个方案更省钱？

查看试题解析
26. 如图，在数轴上，O为原点，点A表示的数为－10，点B表示的数为4．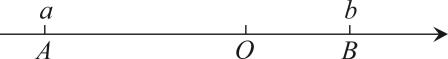

(1)、A，B两点间的距离是．

(2)、若将数轴折叠，使得点A与点B重合，此时原点O与表示数的点重合．

(3)、若点A，B分别以每秒1个单位长度和每秒3个单位长度的速度同时向左运动，则几秒时点B追上点A？

(4)、若点A，B以（3）中的速度相向而行，则几秒时A，B两点相距2个单位长度？

查看试题解析

超出标准（单位：元）	+15	+12	+10	0	-8	-5
卖出数量（单位：箱）	50	20	40	30	30	30