江西省宜春市高安市2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. 中国人最早使用负数，可追溯到两千多年前的秦汉时期， $- \frac{3}{5}$ 的相反数是（）

A、 $- \frac{3}{5}$ B、 $- \frac{5}{3}$ C、 $\frac{3}{5}$ D、 $\frac{5}{3}$

查看试题解析
2. 自从学校开展双减工作，很大的减轻了学生作业负担，同学们有了更多的时间进行课外活动，增强体质．王同学利用“落实双减政策”做了一个正方体展开图，那么在原正方体中，与“减”字所在面相对的面上的汉字是（）

A、落 B、实 C、政 D、策

查看试题解析
3. 下列运算正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $6 a^{3} - 2 a^{3} = 4$ C、 $2 b^{2} + 3 b^{3} = 5 b^{5}$ D、 $4 a^{2} b - 3 b a^{2} = a^{2} b$

查看试题解析
4. 下列运用等式的性质对等式进行的变形中，错误的是（）

A、若 a＝b，则 ac＝bc B、若 a（x²＋1）＝b （x²＋1），则 a＝b C、若 a＝b，则 $\frac{a}{c} = \frac{b}{c}$ D、若 x＝y，则 x－3＝y－3

查看试题解析
5. 《九章算术》记载了这样一道题：“以绳测井，若将绳三折测之，绳多四尺；若将绳四折测之，绳多一尺，问绳长井深各几何？”题意是：用绳子测量水井深度，如果将绳子折成三等份，那么每等份井外余绳四尺：如果将绳子折成四等份，那么每等份井外余绳一尺．问绳长和井深各多少尺？假设井深为x尺，则正确的方程应为（）

A、 $\frac{1}{3} x - 4 = \frac{1}{4} x - 1$ B、3x+4＝4x+1 C、 $\frac{1}{3} x + 4 = \frac{1}{4} x + 1$ D、3（x+4）＝4（x+1）

查看试题解析
6. 如图所示，OB，OC 是∠AOD 的任意两条射线，OM 平分∠AOB，ON 平分∠COD，若∠MON＝α，∠BOC＝β，则表示∠AOD 的代数式是（）

A、2α-β B、α-β C、α+β D、以上都不符合题意

查看试题解析

二、填空题

7. 若 $- \frac{2}{3} a^{2} b^{m}$ 与 $4 a^{n} b$ 是同类项，则 $m + n =$ .

查看试题解析
8. 若 $| a - 1 | + {(b + 2021)}^{2} = 0$ ，那么 $a - b$ 的值是．

查看试题解析
9. 计算： $49 ° 2 7^{'} 5 2^{″} \div 4 =$ ．

查看试题解析
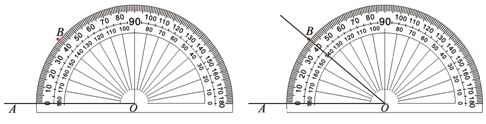
10. 如图，在利用量角器画一个40°的 $∠ A O B$ 的过程中，对于先找点B，再画射线OB这一步骤的画图依据是．

查看试题解析
11. 按照知情同意自愿的原则，我国正积极引导3岁至11岁适龄无禁忌人群“应接尽接”，截至10月29日，该人群已接种新冠疫苗超过353万剂次，则353万用科学记数法表示为.

查看试题解析
12. 如图，两根木条的长度分别为 $6 c m$ 和 $10 c m$ ，在它们的中点处各打一个小孔 $M 、 N$ (小孔大小忽略不计). 将这两根木条的一端重合并放置在同一条直线上，则两小孔间的距离 $M N =$ $c m$ .

查看试题解析

三、解答题

13.

(1)、 $- 1^{4} + 2 \times {(- 3)}^{2} - 5 \div \frac{1}{2} \times 2$ ；

(2)、解方程： $1 - \frac{2 x - 1}{6} = \frac{1 + x}{2}$ ；

查看试题解析
14. 先化简，再求值： $(4 a^{2} - 3 a) - (1 - 4 a + 4 a^{2})$ ，其中 $a = - 2.$

查看试题解析
15. 某粮库6天内粮食进、出库的吨数如下（“ $+$ ”表示进库，“ $-$ ”表示出库） $+ 24$ ， $- 22$ ， $- 13$ ， $+ 34$ ， $- 37$ ， $- 15$

(1)、经过这6天，仓库里的粮食是增加了还是减少了？

(2)、经过这6天，仓库管理仍结算时发现库里还存280吨粮，那么6天前仓库里存粮多少吨？

(3)、如果进出的装卸费都是每吨5元，那么这6天要付多少装卸费？

查看试题解析
16. 有理数a，b，在数轴上的对应点如图所示，将a、b、 $a - b$ 、 $a + b$ 用“＜”号连接起来，并化简代数式： $| a | - | b | - | a + b | + | a - b |$ ．

查看试题解析
17. 方程 $2 - 3 (x + 1) = 0$ 的解与关于x的方程 $\frac{k + x}{2} - 3 k - 2 = 2 x$ 的解互为倒数，求k的值.

查看试题解析
18. 已知多项式 $A = x^{2} + x y + 3 y$ ， $B = x^{2} - x y$ ，

(1)、若 ${(x - 2)}^{2} + | y + 5 | = 0$ ．求 $| 2 A - B |$ 的值；

(2)、若 $2 A - B$ 的值与y的值无关，求x的值．

查看试题解析
19. 我们规定，如果两个角的差是一个直角，那么这两个角互为足角．其中的一个角叫做另一个角的足角．

(1)、如图，直线经过点O，OE平分 $∠ C O B$ ， $O F ⊥ O E$ ．请直接写出图中 $∠ B O F$ 的足角；

(2)、如果一个角的足角等于这个角的补角，求这个角的度数．

查看试题解析
20. 小林到某纸箱厂参加社会实践，该厂计划用50张白板纸制作某种型号的长方体纸箱．如图，每张白板纸可以用A，B，两种方法剪裁，其中A种裁法：一张白板纸裁成4个侧面；B种裁法：一张白板纸裁成2个侧面与4个底面．且四个侧面和两个底面恰好能做成一个纸箱．设按A种方法剪裁的有x张白板纸．

(1)、按B种方法剪裁的有张白板纸；（用含x的代数式表示）

(2)、将50张白板纸裁剪完后，可以制作该种型号的长方体纸箱多少个？

查看试题解析
21. 如图，是由7个大小相同的小立方块搭成的一个几何体.

(1)、请在指定位置画出该几何体从左面、上面看到的形状图；

(2)、若从该几何体中移走一个小立方块，所得新几何体与原几何体相比，从左面、上面看到的形状图保持不变，请画出新几何体从正面看到的形状图．（一种即可）

查看试题解析
22. 如图

(1)、如图1，将两个正方形的一个顶点重合放置，若 $∠ A O D = 40 °$ ，则 $∠ C O B =$ 度；

(2)、如图2，将三个正方形的一个顶点重合放置，求∠1的度数；

(3)、如图3，将三个正方形的一个顶点重合放置，若OF平分 $∠ D O B$ ，那么OE平分 $∠ A O C$ 吗？为什么？

查看试题解析
23. 如图1，点P是线段AB或线段AB延长线上的一点，则图中共有3条线段AP、BP、AB，若其中有一条线段的长是另一条线段长的两倍，则点P是线段AB的“倍分点”．

(1)、一条线段的中点这条线段的“倍分点”；（填“是”或“不是”）

(2)、深入研究：平面内，已知线段AB长为18cm，点P从A点出发，运动的时间为t秒．
①如图2，点P从A点出发，以每秒4cm的速度在线段AB上运动时，求t为何值时，点P是线段AB的“倍分点”？
②如图2，若点P从A点出发，以每秒4cm的速度沿射线AB方向运动，同时点Q从B点出发沿射线AB方向以每秒1cm的速度也运动了t秒，请直接写出点P是线段AQ的“倍分点”时t的值．

查看试题解析