江西省省赣州市大余县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-10 类型:期末考试
一、单选题
-
1. -2的绝对值是()
A、2 B、 C、 D、-22. 下列说法正确的是( )A、的系数是 B、是三次三项式 C、的常数项是1 D、是多项式3. 解方程 , 以下去括号正确的是( )A、 B、 C、 D、4. 小光准备从A地去往B地,打开导航、显示两地距离为37.7km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是( )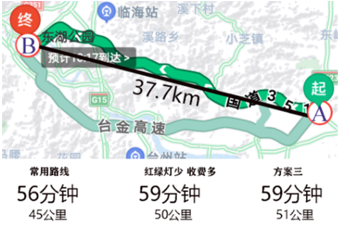 A、两点之间,线段最短 B、垂线段最短 C、三角形两边之和大于第三边 D、两点确定一条直线5. 在明朝程大位《算法统宗》中,有这样的一首歌谣,叫做浮屠增级歌:“远看巍巍塔七层,红光点点倍加增.共灯三百八十一,请问尖头几盏灯?”这首古诗描述的这个宝塔,其古称浮屠,本题说它一共有七层宝塔,每层悬挂的红灯数是上一层的2倍,则这个塔顶有( )盏灯.A、1 B、2 C、3 D、7
A、两点之间,线段最短 B、垂线段最短 C、三角形两边之和大于第三边 D、两点确定一条直线5. 在明朝程大位《算法统宗》中,有这样的一首歌谣,叫做浮屠增级歌:“远看巍巍塔七层,红光点点倍加增.共灯三百八十一,请问尖头几盏灯?”这首古诗描述的这个宝塔,其古称浮屠,本题说它一共有七层宝塔,每层悬挂的红灯数是上一层的2倍,则这个塔顶有( )盏灯.A、1 B、2 C、3 D、7二、多选题
-
6. 若OC是∠AOB内部的一条射线,则下列式子中,能表示“OC是∠AOB的平分线”的是( )A、∠AOC=∠BOC B、∠AOB=2∠BOC C、∠AOC=∠AOB D、∠AOC+∠BOC=∠AOB
三、填空题
-
7. 计算: .8. 已知一个角的补角度数为65°,则这个角的度数是 .9. 央视天下财经2021年11月25日晚报道电影《长津湖》票房突破57亿,截至11月25日,电影《长津湖》已打破此前由影片《战狼2》保持的国产票房最高纪录,以破56.95亿元的成绩成为中国影史票房冠军.将56.95亿用科学记数法表示为 .
 10. 若x=2是关于x的方程2x+3m﹣1=0的解,则m的值等于 .11. 如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.若轮船C在∠APB的平分线上,则轮船C在灯塔P的方向.
10. 若x=2是关于x的方程2x+3m﹣1=0的解,则m的值等于 .11. 如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.若轮船C在∠APB的平分线上,则轮船C在灯塔P的方向. 12. 如图,数轴上A,B两点对应的数分别为10,-3,点P和点Q同时从原点出发,点P以每秒1个单位长度的速度沿数轴正方向运动,点Q以每秒3个单位长度的速度先沿数轴负方向运动,到达B点后再沿数轴正方向运动,当点Q到达点A后,两个点同时结束运动.设运动时间为t秒,当P,Q两点距离为2个单位长度时,t的值为 .
12. 如图,数轴上A,B两点对应的数分别为10,-3,点P和点Q同时从原点出发,点P以每秒1个单位长度的速度沿数轴正方向运动,点Q以每秒3个单位长度的速度先沿数轴负方向运动,到达B点后再沿数轴正方向运动,当点Q到达点A后,两个点同时结束运动.设运动时间为t秒,当P,Q两点距离为2个单位长度时,t的值为 .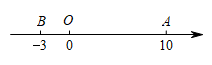
四、解答题
-
13.(1)、计算:(2)、合并同类项:14. 把下列各数填在相应的括号里.
-|-2|,0,-(-1)2 , -(-5), , .
正数集合{___________…};
负数集合{__________…};
非负整数集合{________…}.
15. 如图,点C是线段AB外一点,用尺规作图按下列语句画图:
⑴画射线CA;
⑵连接BC;
⑶在线段AB上找一点D,使BD=BC.
16. 解下列方程:17. 先化简,再求值: , 其中 .18. 某村小麦种植面积是 ,水稻种植面积是小麦种植面积的2倍,玉米种植面积比小麦种植面积少 .(1)、求水稻种植面积比玉米种植面积大多少?(2)、若 ,求三种农作物的种植总面积.19. 面对“新冠疫情”,甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动.已知甲公司有20人,乙公司有30人,第一次甲公司平均每人捐款比乙公司多100元,甲、乙两公司第一次共捐款8000元.
(1)、求第一次甲公司、乙公司平均每人捐款分别为多少元?(2)、为了进一步支持抗击“新冠疫情”,甲、乙两公司全体员工进行了第二次捐款活动,甲公司第二次平均每人捐款在第一次的基础上增加了30%,乙公司第二次平均每人捐款在第一次的基础上增加了元,结果甲、乙两公司第二次共捐款总额比第一次共捐款总额多3000元,求m的值.20. 如图,已知点C是线段AB的中点,点D在线段CB上,且BD=2cm,AD=4cm. (1)、求线段CD的长度;(2)、若将题中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图 , 并求出此时线段CD的长度.21. 观察下列两个等式: , , 给出定义如下:我们称使等式成立的一对有理数a,b为“共生有理数对”,记为 , 如:数对 , , 都是“共生有理数对”.(1)、数对 , 中是“共生有理数对”的是;(2)、若是“共生有理数对”,则“共生有理数对”;(填“是”或“不是”)(3)、若是“共生有理数对”,求的值.22. 阅读材料:我们知道, , 类似地,我们把看成一个整体,则 . “整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
(1)、求线段CD的长度;(2)、若将题中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图 , 并求出此时线段CD的长度.21. 观察下列两个等式: , , 给出定义如下:我们称使等式成立的一对有理数a,b为“共生有理数对”,记为 , 如:数对 , , 都是“共生有理数对”.(1)、数对 , 中是“共生有理数对”的是;(2)、若是“共生有理数对”,则“共生有理数对”;(填“是”或“不是”)(3)、若是“共生有理数对”,求的值.22. 阅读材料:我们知道, , 类似地,我们把看成一个整体,则 . “整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用:
(1)、把看成一个整体,合并;(2)、已知 , 求的值;(3)、已知 , , , 求的值.23. 如图,O是直线PQ上一点,OM是直线PQ上方过点O的一条射线, . 若射线OA在∠MOQ内,∠AOM的大小为 . 射线OB在直线PQ上方,且 .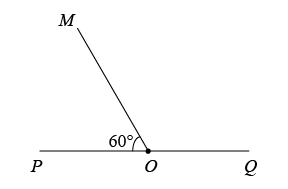

 (1)、用t的代数式表示;(2)、当时,求t的值;(3)、若射线OD在内,且 , 当OA,OB,OD三条射线中的一条射线是另两条射线组成的夹角的平分线时,请求出t的值.
(1)、用t的代数式表示;(2)、当时,求t的值;(3)、若射线OD在内,且 , 当OA,OB,OD三条射线中的一条射线是另两条射线组成的夹角的平分线时,请求出t的值.
-