江西省赣州市寻乌县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-10 类型:期末考试
一、单选题
-
1. 四个有理数﹣1,2,0,﹣3,其中最小的是( )A、﹣1 B、2 C、0 D、﹣32. 为倡导民众环保健康出行,据了解,石城县城区范围内分批次共投放了自助电动小黄车、小蓝车约11000辆,11000这个数用科学记数法表示为( )A、0.11×105 B、1.1×104 C、1.1×103 D、11×1033. 下列计算正确的是( )A、3a+2a=5a2 B、﹣2ab+2ab=0 C、2a3+3a2=5a5 D、3a﹣a=34. 下列生活现象:
①用两个钉子就可以把木条固定在墙上;②从 地道 地架设电线,总是尽可能沿着线段 架设;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④把弯曲的公路改直,就能缩短路程.其中能用“两点之间,线段最短”来解释的现象个数有( )
A、1 B、2 C、3 D、45. 如图所示,正方体的展开图为( ) A、
A、 B、
B、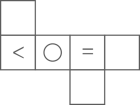 C、
C、 D、
D、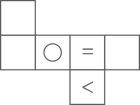 6. 如图是一个运算程序的示意图,若开始输入 的值为81,则第2020次输出的结果为( )
6. 如图是一个运算程序的示意图,若开始输入 的值为81,则第2020次输出的结果为( ) A、3 B、27 C、9 D、1
A、3 B、27 C、9 D、1二、填空题
-
7. 受冷空气影响,我县元旦期间气温下降较大,1月1日最低气温为-2℃,1月2日最低气温是-4℃,最低气温1月2日比1月1日下降了℃.8. 已知方程(a﹣5)x|a|﹣4+2=0是关于x的一元一次方程,则a的值是 .9. 比较大小:20.32°20°30′20″(填“>”“<”或“=”)10. 如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若比大18°,则的度数是度.
 11. 《九章算术》是中国古代的数学专著,奠定了中国传统数学的基本框架.方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”译文:“假设有若干人共同出钱买羊,如果每人出5钱,那么还差45钱;如果每人出7钱,那么仍旧差3钱,求买羊的人数和羊的价钱.”设羊是x钱,可列方程为 .12. 若是数轴上的三点且点表示的数为-2,点表示的数为1,点表示的数为 , 当其中一点到另外两点的距离相等时,则的值为.
11. 《九章算术》是中国古代的数学专著,奠定了中国传统数学的基本框架.方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”译文:“假设有若干人共同出钱买羊,如果每人出5钱,那么还差45钱;如果每人出7钱,那么仍旧差3钱,求买羊的人数和羊的价钱.”设羊是x钱,可列方程为 .12. 若是数轴上的三点且点表示的数为-2,点表示的数为1,点表示的数为 , 当其中一点到另外两点的距离相等时,则的值为.三、解答题
-
13. 计算(1)、(2)、解方程:14. 先化简再求值: , 其中x=1,y=-115. 已知: , .(1)、求;(2)、如果 , 那么C的表达式是什么?16. 如图,在网格中有和点D,请用无刻度的直尺在网格中按下列要求画图.
 (1)、过点D面;(在图①中画)(2)、以点D为顶点作 , 使与互余.(在图② 中只画一个)17. 赣州享有“世界橙乡”的美誉,中华名果赣南脐橙热销世界各地.刚大学毕业的小明把自家的脐橙产品放到了网上售卖,他原计划每天卖100kg脐橙,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负.单位:kg).
(1)、过点D面;(在图①中画)(2)、以点D为顶点作 , 使与互余.(在图② 中只画一个)17. 赣州享有“世界橙乡”的美誉,中华名果赣南脐橙热销世界各地.刚大学毕业的小明把自家的脐橙产品放到了网上售卖,他原计划每天卖100kg脐橙,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负.单位:kg).星期
一
二
三
四
五
六
日
与计划量的差值
+4
-3
-5
+14
-8
+21
-6
(1)、根据记录的数据可知前三天共卖出kg;(2)、根据记录的数据可知销售量最多的一天比销售量最少的一天多销售kg;(3)、若脐橙按4.5元/kg出售,且小明需为买家支付运费(平均0.5元/kg),则小明本周一共赚了多少元?18. 将一副三角板的两个直角顶点重合在一起放置. (1)、如图1,若∠BOC=40°,则∠AOD= , 若OB为∠DOC的角平分线,则∠AOD= .(2)、如图2,∠AOC与∠BOD相等吗?∠AOD和∠BOC有何数量关系?19. 情景:试根据图中信息,解答下列问题:
(1)、如图1,若∠BOC=40°,则∠AOD= , 若OB为∠DOC的角平分线,则∠AOD= .(2)、如图2,∠AOC与∠BOD相等吗?∠AOD和∠BOC有何数量关系?19. 情景:试根据图中信息,解答下列问题: (1)、购买8根跳绳需元,购买14根跳绳需元.(2)、小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.20. 某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:对于三个实数 , 用表示这三个数的平均数,用表示这三个数中的最小的数,例如 , , .请结合上述材料,解决下列问题:(1)、① ,
(1)、购买8根跳绳需元,购买14根跳绳需元.(2)、小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.20. 某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:对于三个实数 , 用表示这三个数的平均数,用表示这三个数中的最小的数,例如 , , .请结合上述材料,解决下列问题:(1)、① ,②.
(2)、若 , 求的值;21. 图1是木工常用的“曲尺”,;现将曲尺顶点O放在直线AB上,曲尺边OM、ON分别在直线AB的左边、右边,过O点在直线AB的左边作射线OC(如图2). (1)、如图2,当曲尺边OM恰好是的平分线时,那么曲尺边ON所在的直线是否平分 , 试说明其理由:(2)、如图3.若OC是的平分线,
(1)、如图2,当曲尺边OM恰好是的平分线时,那么曲尺边ON所在的直线是否平分 , 试说明其理由:(2)、如图3.若OC是的平分线,① ▲ (用含的代数式表示);
②当 , 求的度数.
22. 甲、乙两城相距1000千米,一辆客车从甲城开往乙城,车速为千米/小时,同时一辆出租车从乙城开往甲城,车速为90千米/小时,设客车行驶时间为(小时)(1)、当时,客车与乙城的距离为千米(用含的代数式表示)(2)、已知 , 丙城在甲、乙两城之间,且与甲城相距260千米①求客车与出租车相距100千米时客车的行驶时间;(列方程解答)
②已知客车与出租车在甲、乙之间的服务站处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在处换成客车返回乙城.
是通过计算,分析小王选择哪种方案能更快到达乙城?
23. 已知数轴上有A、B、C三个点对应的数分别是a、b、c , 且满足 ;动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒. (1)、求a、b、c的值;(2)、若点P运动到A、B之间,且到A点距离是到B点距离的2倍,求此时点P的对应的数;若运动到B、C之间时,是否存在点P , 使它到A点距离是到B点距离的2倍,如果存在,请求出它所对应的数,如果不存在,请说明理由;(3)、当点P运动到B点时,点Q从A点出发,以每秒2个单位的速度向终点C点运动,在点Q开始运动后第几秒时,P、Q两点之间的距离为8?请说明理由.
(1)、求a、b、c的值;(2)、若点P运动到A、B之间,且到A点距离是到B点距离的2倍,求此时点P的对应的数;若运动到B、C之间时,是否存在点P , 使它到A点距离是到B点距离的2倍,如果存在,请求出它所对应的数,如果不存在,请说明理由;(3)、当点P运动到B点时,点Q从A点出发,以每秒2个单位的速度向终点C点运动,在点Q开始运动后第几秒时,P、Q两点之间的距离为8?请说明理由.