江西省赣州市石城县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. 化简： $| - 2022 |$ 等于（）

A、2022 B、-2022 C、±2022 D、 $\frac{1}{2022}$

查看试题解析
2. 今年5月11日，国家统计局公布第七次全国人口普查主要数据结果，石城县常住人口约28.32万，数据28.32万用科学记数法表示为（）．

A、28.32×10⁴ B、2.832×10⁵ C、0.2832×10⁶ D、2.832×10⁴

查看试题解析
3. 下列运算中，正确的是（）

A、3x+2y=5xy B、4x-3x=1 C、2ab-ab=ab D、2a+a=2a²

查看试题解析
4. 下列数或式： $(- 2)^{3} ， {(- \frac{1}{3})}^{6} ， - 5^{2} ， 0 ， m^{2} + 1$ ，在数轴上所对应的点一定在原点右边的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
5. 若关于 $x$ 的方程 $\frac{2 x - 1}{3} = 5$ 与 $k x - 1 = 15$ 的解相同，则 $k$ 的值为（）

A、8 B、6 C、-2 D、2

查看试题解析
6. 杨辉是我国南宋时期杰出的数学家和教育家，如图是杨辉在公元1261年著作《详解九章算法》里面的一张图，即“杨辉三角”．它是古代重要的数学成就，比西方的“帕斯卡三角形”早了300多年．请仔细观察计算该图中第n行中所有数字之和为（）

A、2ⁿ^﹣2 B、2ⁿ^﹣1 C、2ⁿ D、2ⁿ⁺¹

查看试题解析

二、填空题

7. 建筑工人在砌墙时，经常在两个墙角分别立一根标志杆，在两根标志杆之间拉一条线，沿这条线就可以砌出直的墙了，其中的数学道理是．

查看试题解析
8. 如果单项式3xmy与-5x³yn是同类项，那么mn= ．

查看试题解析
9. 已知 $∠ a = 29 ° 18'$ ，那么 $∠ a$ 的余角为．

查看试题解析
10. 某种商品每件的进价为80元，标价为120元，后来由于该商品积压，将此商品打七折销售，则该商品每件销售利润为元．

查看试题解析
11. 在国家“双减”政策出台后，同学们的课余生活更加丰富了．为迎接元旦活动，美术兴趣小组要完成学校布置的剪纸作品任务，若每人做5个，则可比计划多9个；若每人做4个，则将比计划少做15个，求这批剪纸作品任务共多少个？若设美术小组共有x人，则这个方程可以列为．

查看试题解析
12. 在同一平面内，∠AOB=120°，射线OC与∠AOB的一边所成夹角为直角，射线OM平分∠BOC，则∠AOM的度数为．

查看试题解析

三、解答题

13. 计算：

(1)、 $4 - 6 - 8 + 10$ ；

(2)、 $[- 3 \times (- \frac{1}{3})^{2} + (- 1)^{3}] \div (- \frac{2}{3})$ ．

查看试题解析
14. 解方程：

(1)、 $2 (3 - 2 x) = 1 - 3 x$ ；

(2)、 $\frac{4 x + 1}{5} + \frac{3 - x}{2} = 1$ ．

查看试题解析
15. 如图，已知平面上三点 $A ， B ， C$ ，请按要求完成下列问题：

⑴画射线 $A C$ ，线段 $B C$ ；

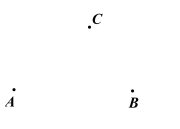
⑵连接 $A B$ ，并用圆规在线段 $A B$ 的延长线上截取 $B D = B C$ ，连接 $C D$ （保留画图痕迹）；

⑶利用刻度尺取线段 $C D$ 的中点 $E$ ，连接 $B E$ .

查看试题解析
16. 如图所示，C是线段AB上的一点，D是AC的中点，E是BC的中点，如果AB=9cm，AC=5cm.
求：

(1)、AD的长；

(2)、DE的长.

查看试题解析
17. 石城县矿山机械设备闻名省内外．在某矿山机械设备车间工人正在紧张地按订单进度进行生产，若每人每天平均可以生产轴承12个或者轴杆16个，1个轴承与2个轴杆组成一套，该车间共有90人，应该怎样调配人力，才能使每天生产的轴承和轴杆正好配套？

查看试题解析
18. 为改善居民居住条件，让人民群众生活更方便更美好，国家出台了改造提升城镇老旧小区政策．在我县“老城换新颜”小区改造中，某小区规划修建一个广场 $($ 平面图形如图所示 $)$ ：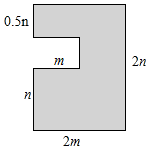

(1)、用含 $m$ ， $n$ 的代数式表示广场 $($ 阴影部分 $)$ 的面积 $S$ ；

(2)、若 $m = 60$ 米， $n = 50$ 米，求出该广场的面积．

查看试题解析
19. 如图， $O$ 为直线 $A B$ 上的一点， $∠ A O C = 48 °$ ， $O D$ 平分 $∠ A O C$ ， $∠ D O E = 90 °$ ．

(1)、求 $∠ B O D$ 的度数；

(2)、 $O E$ 是 $∠ B O C$ 的平分线吗？为什么？

查看试题解析
20. 老师在黑板上写了一个正确的演算过程，随后用手掌捂住了多项式形式如下：
$+ 2 (a^{2} - 4 a b + 4 b^{2}) = 3 a^{2} + 2 b^{2}$

(1)、求所捂的多项式；

(2)、若a，b满足： $(a + 1)^{2} + | b - \frac{1}{2} | = 0$ ，请求出所捂的多项式的值．

查看试题解析
21. 阅读材料：
我们知道， $2 x + 3 x - x = (2 + 3 - 1) x = 4 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $2 (a + b) + 3 (a + b) - (a + b) = (2 + 3 - 1) (a + b) = 4 (a + b)$ ． “整体思想”是中学数学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．

(1)、尝试应用：
把 ${(x - y)}^{2}$ 看成一个整体，求将 $2 {(x - y)}^{2} - 4 {(x - y)}^{2} + {(x - y)}^{2}$ 合并的结果；

(2)、已知 $2 m - 3 n = 3$ ，求代数式 $4 m - 6 n + 5$ 的值；

(3)、拓广探索：
已知 $a - 2 b = 4$ ， $b - c = - 2$ ， $3 c + d = 6$ ，求 $(a + 3 c) - (2 b + c) + (b + d)$ 的值．

查看试题解析
22. 为了提升公民的节水意识，保护水资源，各地一般采用价格调控的手段达到节水的目的．某市自来水收费的收费标准如下表：
每月用水量
单价（元/立方米）
不超过16立方米的部分
3
超过16立方米不超过24立方米的部分
4
超过24立方米的部分
6.5

(1)、在某户居民2月份用水12立方米，则应收水费多少元？

(2)、若某户居民4月份用水m立方米（其中16＜m≤24），请用含有m的代数式表示应收水费．

(3)、某户居民5、6月份共用水40立方米（5月份用水量超过了16立方米），设6月份用水n立方米，请用含有n的代数式表示该居民5、6两个月共交水费多少元？

查看试题解析
23. 点 $O$ 为直线 $A B$ 上一点，将一直角三角板 $O M N$ 的直角顶点放在点 $O$ 处．射线 $O C$ 平分 $∠ M O B$ ．

(1)、如图1，若 $∠ A O M = 30 °$ ，求 $∠ C O N$ 的度数；

(2)、在图1中，若 $∠ A O M = a$ ，直接写出 $∠ C O N$ 的度数 $($ 用含 $a$ 的代数式表示 $)$ ；

(3)、将图1中的直角三角板 $O M N$ 绕顶点 $O$ 顺时针旋转至图2的位置，一边 $O M$ 在射线 $O B$ 上方，另一边 $O N$ 在直线 $A B$ 的下方．
①探究 $∠ A O M$ 和 $∠ C O N$ 的度数之间的关系，写出你的结论，并说明理由；（提示：可设 $∠ A O M = a$ ）
②当 $∠ A O C = 3 ∠ B O N$ 时，求 $∠ A O M$ 的度数．

查看试题解析

每月用水量	单价（元/立方米）
不超过16立方米的部分	3
超过16立方米不超过24立方米的部分	4
超过24立方米的部分	6.5