江西省赣州市南康区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的绝对值等于（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、2 D、－2

查看试题解析
2. 尼莫点，正式名称为海洋难抵极，是地球表面距离陆地最偏远的地点，位于南太平洋中央的海面上，最近的陆地与当地相隔2688000米之遥，其中2688000用科学记数法表示应为（）

A、2.688×10⁷ B、26.88×10⁵ C、2.688×10⁶ D、0.2688×10⁷

查看试题解析
3. 下列说法：① $x^{2} - 3 x y + y^{2}$ 是二次三项式；② $2 a^{2} b^{3}$ 与 $3 a^{3} b^{2}$ 是同类项；③ $2^{3} x a b^{3}$ 的次数是6；④ $- 2 π x y^{2}$ 的系数是－2．其中说法正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 解一元一次方程 $\frac{1}{2} (x + 1) = 1 - \frac{1}{3} x$ 时，去分母正确的是（）

A、 $3 (x + 1) = 1 - 2 x$ B、 $2 (x + 1) = 1 - 3 x$ C、 $2 (x + 1) = 6 - 3 x$ D、 $3 (x + 1) = 6 - 2 x$

查看试题解析
5. 如图，这是由大小相同的长方体木块搭成的立体图形，则从正面看这个立体图形，得到的平面图形是（）

A、 B、 C、 D、

查看试题解析
6. 一项工程，甲单独做5天完成，乙单独做8天完成．若甲先做1天，然后甲、乙合作完成了此项工作，设乙做了 $x$ 天，则可列方程为（）

A、 $\frac{x + 1}{5} - \frac{x}{8} = 1$ B、 $\frac{x + 1}{5} + \frac{x}{8} = 1$ C、 $\frac{x - 1}{5} - \frac{x}{8} = 1$ D、 $\frac{x - 1}{5} + \frac{x}{8} = 1$

查看试题解析

二、填空题

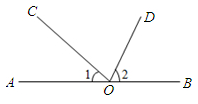
7. 一个单项式中只含字母a、b且单项式次数为4，请你写出三个符合条件的不同类型的单项式：、、．（说明：xy与－2xy可看成同一类型）

查看试题解析
8. 方程 $\frac{1}{2} x - 1 = 3$ 和方程 $\frac{1}{2} x + m = 0$ 的解相同，则m＝．

查看试题解析
9. 已知a＋b＝2021，ab＝3，则（3a－2b）－（－5b＋ab）的值为．

查看试题解析
10. 如图，O是AB上一点，OD平分∠BOC，∠1＝20°，∠2的度数是．

查看试题解析
11. 明代数学家程大位的《算法统宗》中有这样一个问题，其大意为；有一群人分银子，如果每人分七两，则剩余四两；如果每人分九两，则还差八两，请问：所分的银子共有两．

查看试题解析
12. 若A、B、P是数轴上三点，且点A表示的数为﹣1，点B表示的数为3，点P表示的数为x ，当其中一点到另外两点的距离相等时，则x的值可以是

查看试题解析

三、解答题

13. 解答：

(1)、计算： $| - 8 | \div 2 - (- 3)^{2} \times 5$ ；

(2)、读下列语句并画图：
①直线a经过A，B两点；
②点P是直线a外一点，过点P的直线b与直线a相交于点C，并使点C在线段AB上；
③画射线CD．

查看试题解析
14. 先化简再求值： $(3 a^{2} b - a b^{2}) - 2 (a b^{2} - 3 a^{2} b) + 3 a b^{2}$ ，其中 $a = - 2$ ， $b = - 3$ ．

查看试题解析
15. 解方程： $\frac{1 - 2 x}{3} = \frac{3 x + 1}{7} - 3$

查看试题解析
16. 快递小哥骑摩托车从快递公司出发负责送货，向东走了4千米到达小明家，继续走了1.5千米到达小红家，又向西走了10千米到达小丽家，最后回到快递公司．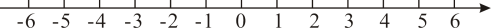

(1)、以快递公司为原点，以向东的方向为正方向，用1个单位长度表示1千米，请你在数轴轴上标出小明、小红、小丽家的位置；

(2)、小明家与小丽家相距多远？

(3)、若摩托车每千米耗油0.03升，那么快递小哥这次送货共耗油多少升？

查看试题解析
17. 一个小立方体的六个面分别标有字母A，B，C，D，E，F，从三个不同方向看到的情形如图所示.

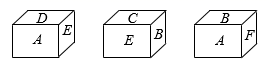(1)、A对面的字母是， B对面的字母是， E对面的字母是.（请直接填写答案）

(2)、若A=2x-1， $B = - 3 x + 9$ ， C=-7，D=1，E=2x＋5，F= -9，且字母E与它对面的字母表示的数互为相反数，求A，B的值.

查看试题解析
18. 点C在线段AB上，点M是AC的中点，AM=1，BC=4．

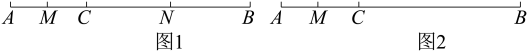(1)、如图1，若点N是BC的中点，求MN的长度；

(2)、如图2，若点N在射线AB上，AN=7，请补全图形，并直接写出BN的长度是 ▲ ．

查看试题解析
19. 赣州享有“世界橙乡”的美誉，中华名果赣南脐橙热销世界各地，2019年赣南脐橙又一次迎来大丰收，现果农们对脐橙进行装箱打包运往市场销售，第一天完成了这批脐橙的 $\frac{2}{5}$ ，第二天完成了剩余脐橙的 $\frac{3}{4}$ ，最后还剩下180千克没有完成装箱，求这批脐橙共有多少千克?

查看试题解析
20. 某水果店用600元购进甲、乙两种脐橙共160kg，这两种脐橙的进价、售价如下表所示：

进价（元/kg）
售价（元/kg）
甲种
3
4
乙种
4
6

(1)、这两种脐橙各购进多少千克？

(2)、如果除了进货成本，水果店还需要0.1元/kg的其他销售费用，那么销售完这两种脐橙可以获得多少利润？

查看试题解析
21. 如图，将一副三角尺按甲、乙、丙、丁四种不同方式摆放．

(1)、在的摆放方式中∠ $α$ 与∠ $β$ 互余；在的摆放方式中∠ $α$ 与∠ $β$ 互补．

(2)、在哪种摆放方式中∠ $α$ 与∠ $β$ 相等？请说明理由．

查看试题解析
22. 如图1所示，将两块直角三角尺的直角顶点C叠放在一起．

(1)、若∠DCE＝25°，则∠ACB＝°；若∠ACB＝130°，则∠DCE＝°．

(2)、如图2所示，若两个同样的三角板，将60°锐角的顶点A叠放在一起，则∠DAB与∠CAE有何数量关系，请说明理由．

(3)、如图3所示，已知∠AOB＝ $α$ ， ∠COD＝ $β$ （ $α$ ， $β$ 都是锐角）．若把它们的顶点O叠放在一起，将∠AOD与∠BOC的数量关系用含 $α$ 与 $β$ 的式子表示出来，直接写出结论．

查看试题解析
23. 【观察发现】如图，我们通过观察后可以发现：两条直线相交，最多有1个交点；三条直线相交，最多有3个交点；那么四条直线相交，最多有 ▲ 个交点；n条直线相交，最多有 ▲ 个交点（用含n的代数式表示）；
【实践应用】在实际生活中同样存在数学规律型问题，请你类比上述规律探究，计算：某校七年级举办篮球比赛，第一轮要求每两班之间比赛一场，若七年级共有16个班，则这一轮共要进行多少场比赛？

查看试题解析
24. 一张长方形的餐桌可以坐6个人，按照下图的方式摆放餐桌和椅子：

(1)、观察表中数据规律填空：a＝， b＝， c＝；
餐桌张数
1
2
3
4
5
…
n
可坐人数
6
8
10
a
b
…
c

(2)、一家酒楼，按上图的方式拼桌，要使拼成的一张大餐桌刚好能坐160人，请问需几张餐桌拼成一张大餐桌？

(3)、若酒店有240人来就餐，还有更好的拼桌方式吗？最少要用多少张餐桌？如果有，画出此时拼桌方式的示意图；如果没有，请说明理由．

查看试题解析

	进价（元/kg）	售价（元/kg）
甲种	3	4
乙种	4	6

餐桌张数	1	2	3	4	5	…	n
可坐人数	6	8	10	a	b	…	c