江西省赣州市赣县区2021-2022学年七年级上学期期末数学试题
试卷更新日期：2022-11-10 类型：期末考试
一、单选题
-
1. -20的相反数是（ ）A、20 B、-20 C、 D、2. 据统计，2021年赣县区户籍总人口约为65.4万人，65.4万用科学记数法表示为（ ）A、654×103 B、65.4×104 C、6.54×105 D、6.54×1063. 中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数．如图，根据刘徽的这种表示法，观察图①，可推算图②中所得的数值为（ ）
A、﹣3 B、﹣2 C、﹣6 D、+64. 下列运算正确的是（ ）．A、2a-a＝1 B、2a+b＝3ab C、2a+3a＝5a D、3a2+2a2＝5a45. 有理数a，b在数轴上对应点的位置如图所示，下列各式正确的是（ ）
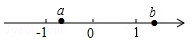A、 B、 C、 D、6. 如图是2022年1月的日历，洋洋用长方形从中任意的框出三个日期，若这三个日期的和是54，则C处的日期为1月（ ）日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
A、24日 B、25日 C、26日 D、27日二、填空题
-
7. 如图，木匠师傅经过刨平的木板上的A，B两个点，可以弹出一条笔直的墨线，能解释这一实际应用的数学基本事实是 ．
8. 一副三角板按如图所示的方式摆放，∠1＝67.5°，则∠2的度数为 ．
9. 若3xm-1y与-5x2yn+3是同类项，则（m+2n）2021＝ ．10. 当 时，关于x的方程 的解是11. 我国元朝朱世杰所著的《算学启蒙》（1299年）一书，有一道题目是：“今有良马日行二百四十里，驽马日行一百五十里．驽马先行一十二日，问良马几何日追及之．”译文是：“跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，快马几天可以追上慢马?”若慢马和快马从同一地点出发，设快马x天可以追上慢马，则可以列方程为 ．12. 从点O引出三条射线OA ， OB ， OC ， 已知∠AOB=30°，在这三条射线中，当其中一条射线是另两条射线所组成角的平分线时，则∠AOC= ．13. 一个角的余角比这个角的补角的 还小10°，则这个角的度数是 ．三、解答题
-
14. 计算(1)、-（-3）+|-1|-（+9）；(2)、[ 3×（-）2+（-1）3]÷（-）．15. 解下列方程： ．16. 如图所示，已知点A、B、C是网格上的三个格点，请仅用无刻度直尺作图：
(1)、画射线AC；(2)、画线段AB；(3)、过点B画射线BE，使得BE∥AC．17. 先化简，再求值：2（3ab2-a3b）-3（2ab2-a3b），其中a＝- ， b＝4．18. 小王购买了一套经济适用房，他准备将地面铺上地砖，地面结构如图所示：根据图中的数据（单位：m），解答下列问题：
(1)、用含x、y的代数式表示地面总面积S；(2)、当y=1.5，且客厅面积比卫生间面积多21m2 ． 若铺1m2地砖的平均费用为100元，那么铺地砖的总费用为多少元？19. 用“⊕”定义一种新运算：对于任意有理数a和b，规定a⊕b＝ab2+2ab+a.如：1⊕3＝1×32+2×1×3+1＝16.(1)、求（﹣1）⊕2的值；(2)、若a⊕3=4，求a的值20. 如图，线段AB上顺次有三个点C，D，E，把线段AB分为了2：3：4：5四部分，且AB=28，
(1)、求线段AE的长；(2)、若M，N分别是DE，EB的中点，求线段MN的长度．21. 如图O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°.
(1)、求∠BOD的度数；(2)、试判断OE是否平分∠BOC，并说明理由.22. 为鼓励民众节约用电，城镇居民生活用电电费目前实行梯度收费，具体标准如下表：月用电量（单位：千瓦时）
单价（单位：元）
150以内（含150）
0.5
超过150但不超过300的部分（含300）
0.6
300以上（不含300）的部分
0.8
(1)、若月用电100千瓦时，应交电费多少元？若月用电200千瓦时，应交电费多少元？(2)、若某用户12月应交电费93元，该用户12月的用电量是多少？23. 如图，已知A、B、C是数轴上三点，点O为原点，点C表示的数为6，BC＝4， AB＝12．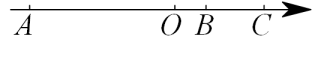
(1)、写出数轴上点A、B表示的数；(2)、动点P、Q分别从A、C同时出发，沿数轴向右匀速运动．点P的速度是每秒6个单位长度，点Q的速度是每秒3个单位长度，点M为AP的中点，点N在线段CQ上，且CN＝CQ，设运动时间为t（t＞0）秒．①求数轴上点M、N表示的数（用含t的式子表示）；
②当M、B、N三个点中的其中一个点是另两点构成的线段的中点的时候，求t的值．
24. 为庆祝“元旦”，光明学校统一组织合唱比赛，七、八年级共92人（其中七年级的人数多于八年级的人数，且七年级的人数不足90人）准备统一购买服装参加比赛．如表是某服装厂给出服装的价格表：购买服装的套数
1套至45套
46套至90套
91套以上（含91套）
每套服装的价格
60元
50元
40元
(1)、如果两个年级分别单独购买服装一共应付5000元，求七、八年级各有多少学生参加合唱比赛；(2)、如果七年级参加合唱比赛的学生中，有10名同学抽调去参加绘画比赛，不能参加合唱比赛，请你为两个年级设计一种最省钱的购买服装方案．