浙江省温州市瑞安市西部联考2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-11-10 类型:期中考试
一、单选题
-
1. 实数中, 最小的数是( )A、 B、0 C、 D、22. 已知的半径为5 , 若 , 则点在( )A、圆内 B、圆上 C、圆外 D、无法判断3. 任意抛掷一枚均匀的骰子, 结果朝上一面的点数为2的倍数的概率是( )A、 B、 C、 D、4. 把抛物线向下平移1个单位, 所得拋物线的表达式为( )A、 B、 C、 D、5. 如图,是的半径, 以为直径的与的弦相交于点 , 则与 的大小关系( )
 A、 B、 C、 D、无法判断6. 已知二次函数的部分图象如图所示, 若 , 则的取值的范围是( )
A、 B、 C、 D、无法判断6. 已知二次函数的部分图象如图所示, 若 , 则的取值的范围是( ) A、 B、 或 C、 D、7. 一个袋子中装有12个球 (袋中每个球除颜色外其余都相同). 某活动小组想估计袋子中红球的个数, 分10个组进行摸球试验, 每一组做400次试验, 汇总后, 摸到红球的次数为 3000次. 请你估计袋中红球接近( )A、3 B、4 C、6 D、98. 已知二次函数 , 其函数值与自变量之间的部分对应值如表所示:
A、 B、 或 C、 D、7. 一个袋子中装有12个球 (袋中每个球除颜色外其余都相同). 某活动小组想估计袋子中红球的个数, 分10个组进行摸球试验, 每一组做400次试验, 汇总后, 摸到红球的次数为 3000次. 请你估计袋中红球接近( )A、3 B、4 C、6 D、98. 已知二次函数 , 其函数值与自变量之间的部分对应值如表所示:0
1
2
3
4
0
点在函数的图象上, 当时, 与的大小关系正确的是( )
A、 B、 C、 D、9. 如图,在中,为直径,点为圆上一点, 将劣弧沿弦翻折交于点 , 连接 . 若点与圆心不重合, , 则的度数为( ) A、 B、 C、 D、10. 如图, 将抛物线沿轴翻折, 翻折前后的两条抛物线构成一个新图象.若直线与这个新图象有3个公共点, 则的值为( )
A、 B、 C、 D、10. 如图, 将抛物线沿轴翻折, 翻折前后的两条抛物线构成一个新图象.若直线与这个新图象有3个公共点, 则的值为( ) A、或2 B、或2 C、2或4 D、或4
A、或2 B、或2 C、2或4 D、或4二、填空题
-
11. 分解因式: =12. 抛物线的顶点坐标是 .13. 如图,是的直径,是上的两点, 分别连结 , , 则的度数为 .
 14. 如图,甲, 乙两个转盘分别被三等分、四等分,各转动一次,停止转动后,将指针指向的数字分别记为 , 使抛物线与轴有公共点的概率为 .
14. 如图,甲, 乙两个转盘分别被三等分、四等分,各转动一次,停止转动后,将指针指向的数字分别记为 , 使抛物线与轴有公共点的概率为 . 15. 已知抛物线 (k为常数,且k≤3),当-1≤x≤3时,该抛物线对应的函数值有最大值-7,则k的值为 .16. 图1是郑州的网红打卡点 “戒指桥”, 其数学模型如图2所示. 线段是其中一条拉索, 点在圆上, 点是圆和水平桥面的交点. 小明测得 , 且在 B点和点观测点的仰角均为 , 则点到桥面的距离为 , “戒指” 的半径为 .
15. 已知抛物线 (k为常数,且k≤3),当-1≤x≤3时,该抛物线对应的函数值有最大值-7,则k的值为 .16. 图1是郑州的网红打卡点 “戒指桥”, 其数学模型如图2所示. 线段是其中一条拉索, 点在圆上, 点是圆和水平桥面的交点. 小明测得 , 且在 B点和点观测点的仰角均为 , 则点到桥面的距离为 , “戒指” 的半径为 .
三、解答题
-
17.(1)、计算: .(2)、解不等式 ,并把解集表示在数轴上
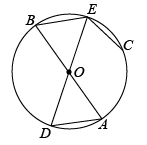
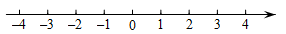 18. 已知:如图, , 是的直径,C是上一点,且 .
18. 已知:如图, , 是的直径,C是上一点,且 .求证: .
 19. 已知抛物线过两点.(1)、求该拋物线的函数表达式;(2)、试判断点是否在此函数图象上.20. 的顶点都在正方形网格格点上,如图所示.
19. 已知抛物线过两点.(1)、求该拋物线的函数表达式;(2)、试判断点是否在此函数图象上.20. 的顶点都在正方形网格格点上,如图所示.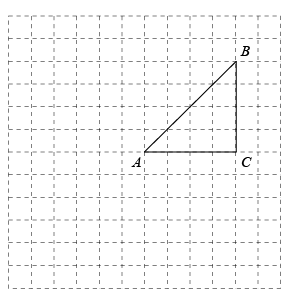 (1)、将绕点A顺时针方向旋转得到(点对应点), 画出 .(2)、请找出过三点的圆的圆心, 标明圆心的位置.21. 一个不透明的布袋里装有1个白球,2 个红球,它们除颜色外其余都相同。(1)、从中任意摸出1个球,记下颜色后放回,搅匀,再任意摸出一个球,求两次都摸出红球的概率(要求画树状图或列表)(2)、若加入若干个除颜色外完全相同的黑球后,从中任意摸出1个球,是红球的概率的 , 求加入的黑球的个数.22. 已知拋物线经过点 .(1)、如果此抛物线同时经过 , 求抛物线的对称轴.(2)、将拋物线的顶点A先向右平移1个单位, 再向下平移1个单位后恰好与拋物线上的点B重合,求a的值.23. 某公司生产中考专用跳绳, 每条需要成本50元, 销售单价不低于62元, 且不高于80元. 根据市场调研, 当每条定价为70元时, 日均销量为1100条, 销售单价每提高1元, 则日均销售量减少50条.(1)、求出该跳绳的日均销量与销售单价之间的函数关系式.(2)、当跳绳的单价定为多少元时, 公司所获的总利润最大? 最大利润为多少元?(3)、公司决定每销售一条跳绳, 就捐赠元给农村留守儿童基金会. 捐款后,公司的日销售利润最少为13500元, 求的值.24. 如图1,已知是的直径,内接于 , 点是一动点 (点不与点重合).
(1)、将绕点A顺时针方向旋转得到(点对应点), 画出 .(2)、请找出过三点的圆的圆心, 标明圆心的位置.21. 一个不透明的布袋里装有1个白球,2 个红球,它们除颜色外其余都相同。(1)、从中任意摸出1个球,记下颜色后放回,搅匀,再任意摸出一个球,求两次都摸出红球的概率(要求画树状图或列表)(2)、若加入若干个除颜色外完全相同的黑球后,从中任意摸出1个球,是红球的概率的 , 求加入的黑球的个数.22. 已知拋物线经过点 .(1)、如果此抛物线同时经过 , 求抛物线的对称轴.(2)、将拋物线的顶点A先向右平移1个单位, 再向下平移1个单位后恰好与拋物线上的点B重合,求a的值.23. 某公司生产中考专用跳绳, 每条需要成本50元, 销售单价不低于62元, 且不高于80元. 根据市场调研, 当每条定价为70元时, 日均销量为1100条, 销售单价每提高1元, 则日均销售量减少50条.(1)、求出该跳绳的日均销量与销售单价之间的函数关系式.(2)、当跳绳的单价定为多少元时, 公司所获的总利润最大? 最大利润为多少元?(3)、公司决定每销售一条跳绳, 就捐赠元给农村留守儿童基金会. 捐款后,公司的日销售利润最少为13500元, 求的值.24. 如图1,已知是的直径,内接于 , 点是一动点 (点不与点重合).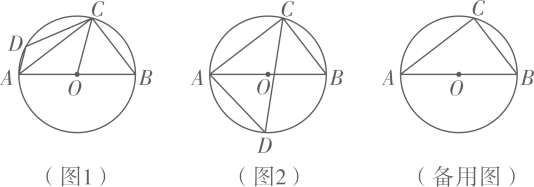 (1)、若 , 连结 , 求证: .(2)、在(1)的条件下,求的长.(3)、如图2,若平分 , 连结 , 求的面积.(4)、当为何值时,为等腰三角形?
(1)、若 , 连结 , 求证: .(2)、在(1)的条件下,求的长.(3)、如图2,若平分 , 连结 , 求的面积.(4)、当为何值时,为等腰三角形?