福建省南平市浦城县2022-2023学年七年级上学期期中考试数学试题

试卷更新日期：2022-11-10 类型：期中考试

进入出卷网下载

一、单选题

1. 实数2的相反数是（）

A、-2 B、2 C、 $\pm 2$ D、 $\frac{1}{2}$

查看试题解析
2. $2^{3}$ 可以表示为（）

A、 $2 + 2 + 2$ B、 $2 \times 2 \times 2$ C、 $2 \times 3$ D、 $3 \times 3$

查看试题解析
3. 计算 $- 2 a^{2} + 5 a^{2}$ 的结果为（）

A、 $3 a^{2}$ B、 $- 7 a^{2}$ C、 $3 a^{4}$ D、 $- 10 a^{4}$

查看试题解析
4. 北京时间2019年4月10日21点整，天文学家召开全球新闻发布会，宣布首次直接拍摄到黑洞的照片，这颗黑洞位于代号为 $M 87$ 的星系当中，距离地球 $53000000$ 光年之遥，质量相当于60亿颗太阳，其中 $53000000$ 这个数据可以用科学记数法表示为（）

A、 $5.3 \times 1 0^{8}$ B、 $5.3 \times 1 0^{7}$ C、 $5.3 \times 1 0^{8}$ D、 $53 \times 1 0^{2}$

查看试题解析
5. 下列各组单项式中，不是同类项的一组是（）

A、 $x^{2} y$ 和 $2 x y^{2}$ B、 $- 3^{2}$ 和3 C、 $3 x y$ 和－ $\frac{x y}{2}$ D、 $5 x^{2} y$ 和 $- 2 y x^{2}$

查看试题解析
6. 下列变形中，错误的是（）

A、若2x=x-3，则x=-3 B、若6x=-3，则x=-2 C、若 $\frac{1}{2} x$ =1，则x=2 D、若2x-3=x+2，则x=5

查看试题解析
7. 下列说法中正确的是（）

A、0是最小的整数 B、1.30×10⁴精确到百分位 C、单项式 $\frac{2}{3} π x^{2}$ 的系数是 $\frac{2}{3}$ D、x³-2x²y²+3y²是四次三项式

查看试题解析
8. 下列方程的解是 $x = 3$ 的有（）
① $- 2 x - 6 = 0$ ② $| x + 2 | = 5$ ③ $(x - 3) (x - 1) = 0$ ④ $\frac{1}{3} x = x - 2$

A、1个 B、2个 C、3 D、4个

查看试题解析
9. 已知 $| x | = 5$ 、 $| y | = 3$ ，并且 $x > y$ ，则 $x + y$ 的值是（）

A、-2 B、8 C、2或8 D、-2或-8

查看试题解析
10. 一根1m长的小棒，第一次截去它的 $\frac{1}{2}$ ，第二次截去剩下的 $\frac{1}{2}$ ，如此截下去，第五次后剩下的小棒的长度是（）

A、 $\frac{1}{2}$ m B、 $\frac{1}{\begin{array}{l} 5 \end{array}}$ m C、 $\frac{1}{16}$ m D、 $\frac{1}{32}$ m

查看试题解析

二、填空题

11. 如果节约20元钱，记作“ $+ 20$ ”元，那么浪费12元钱，记作元.

查看试题解析
12. 方程 $x^{n + 2} = 7$ 是关于x的一元一次方程，则 $n =$ ．

查看试题解析
13. 某种商品每件的定价为m元，商店在节日搞促销活动，降价20%，促销期间每件商品实际售价为元．

查看试题解析
14. 若 $x$ ， $y$ 为有理数，且 $| x + 2 | + {(y - 2)}^{2} = 0$ ，则 $x + y =$

查看试题解析
15. 已知代数式x－3y的值是 5，则代数式2x－6y－1的值是.

查看试题解析
16. 按照如图所示的操作步骤，若输入的值为3，则输出的值为．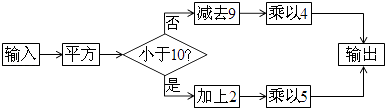

查看试题解析

三、解答题

17. 把下列各数填入相应括号：
$- \frac{2}{3}$ ， $0.218$ ， $- 4.14$ ， $2022$ ， $- 25$ ， $55 %$ ， $0$ ．
正分数：{                   }；
整数：{                   }；
负有理数：{                   }；
非负数：{                   }．

查看试题解析
18. 把下列各数在数轴上表示出来，并按从小到大的顺序用“＜”连接起来.
﹣1.5，0，﹣3 $\frac{1}{2}$ ，2.5，﹣（﹣1），﹣|﹣4|.

查看试题解析
19. 计算或化简

(1)、 $- 5 + 4 + 8 - 6$

(2)、 $(- 3) \times 2 + 6 \div (- \frac{1}{2})$

(3)、 $(\frac{3}{4} + \frac{5}{9} - \frac{7}{12}) \times 36$

(4)、 $- 1^{4} - 6 \div (- 2) \times | - \frac{1}{3} |$

(5)、 $4 a - 3 b - 5 a + 2 b$

(6)、 $3 (2 a - 7 b) - 2 (a + 3 b)$

查看试题解析
20. 先化简，再求值： $\frac{1}{2} x - 2 (x - \frac{1}{3} y^{2}) + (- \frac{1}{2} x + \frac{1}{3} y^{2})$ ，其中 $x = - 2 ， y = \frac{2}{3}$ ．

查看试题解析
21. 如图，一块边长为 $x$ 米（ $x$ ＞4）正方形的铁皮，如果截去一个长4米，宽3米的一个长方形.

(1)、用含 $x$ 的代数式表示阴影部分的面积.

(2)、当 $x$ =6时，求阴影部分的面积.

(3)、直接写出阴影部分的周长（用含x的代数式表示）.

查看试题解析
22. 在日常工作中，洒水车每天都道路上来回洒水．我们约定洒水车在行驶过程中，向北的行程记为正数，向南的行程记为负数． 2022年9月20日这一天，某台洒水车从市政工程处出发，所走的路程（单位：千米）为： $+ 5$ ， $+ 7.5$ ， $- 8$ ， $- 3$ ， $+ 9.5$ ， $+ 2.5$ ， $- 11$ ， $- 3.5$ 问：

(1)、这天收工时，这台洒水车离市政工程处多远？它在市政工程处的南边还是北边？

(2)、这台洒水车这一天共行车多少千米？

(3)、若洒水车每走1千米耗油0.2升，请问这一天这台洒水车在洒水过程中耗油多少升？

查看试题解析
23. 观察下列等式：
第1个等式： $a_{1} = \frac{1}{1 \times 3} = \frac{1}{2} \times （ 1 - \frac{1}{3} ）$ ；

第2个等式： $a_{2} = \frac{1}{3 \times 5} = \frac{1}{2} \times （ \frac{1}{3} - \frac{1}{5} ）$ ；

第3个等式： $a_{3} = \frac{1}{5 \times 7} = \frac{1}{2} \times （ \frac{1}{5} - \frac{1}{7} ）$ ；

第4个等式： $a_{4} = \frac{1}{7 \times 9} = \frac{1}{2} \times （ \frac{1}{7} - \frac{1}{9} ）$ ；

…

请解答下列问题：

(1)、按以上规律列出第5个等式：a₅==；

(2)、用含有n的代数式表示第n个等式：a_n==（n为正整数）；

(3)、求a₁+a₂+a₃+a₄+…+a₁₀₀的值.

查看试题解析
24. 阅读下面材料．
如图1，若线段 $A B$ 在数轴上， $A$ 、 $B$ 两点表示的数分别是 $a$ ， $b$ $(b > a)$ ，则线段 $A B$ 的长（点 $A$ 到点 $B$ 的距离）可表示为 $A B = b - a$ ．

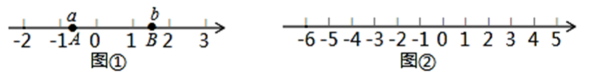
请用上面的材料中的知识解答下面的问题：

如图2，一个点从数轴上的原点开始，先向左移动2个单位长度到达A点，再向右移动6个单位长度到达B点．

(1)、此时点A在数轴上表示的数为；点B在数轴上表示的数为；

(2)、若点A、B分别以每秒1个单位长度和2个单位长度的速度匀速移动，设移动时间为 $t$ 秒．
①若点A向右移动，点B向左移动，则点A表示的数是，点B表示的数是（含 $t$ 的式子表示），当 $t$ 为秒时它们相遇；

②若点A向左移动，点B向右移动，则点A表示的数是，点B表示的数是（含 $t$ 的式子表示），设运动时间为 $t$ 秒，则当 $t$ 为秒时 $A B = 15$ ．

查看试题解析