浙江省舟山市定海区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. 2022的相反数是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 有理数5，-2，0，-4中最小的一个数是（）

A、5 B、-2 C、0 D、-4

查看试题解析
3. 我国第七次人口普查显示，全国总人口约为1411000000人，将这个总人口数用科学记数法表示为（）

A、14.11×10⁷ B、1.411×10⁸ C、1.411×10⁹ D、0.1411×10¹⁰

查看试题解析
4. 下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个角的是（）

A、 B、 C、 D、

查看试题解析
5. 下列各组中的两个代数式属于同类项的是（）

A、 $3 x y$ 与 $- \frac{1}{2} x^{2} y$ B、 $- 2.1$ 与 $\frac{3}{4}$ C、 $2 a^{3} b$ 与 $2 a b^{3}$ D、 $3 a b^{2}$ 与 $0.001 b a^{2}$

查看试题解析
6. 若 $x = 3$ 是关于x的方程 $2 x + a = 4$ 的解，则a的值为（）

A、-10 B、-2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
7. 某商品因换季准备打折销售，如果按定价的七五折出售，将亏本35元，而按定价的九五折出售，将赚25元．设这种商品的定价为x元，可列方程为（）

A、75%x-35=95%x+25 B、75%x+35=95%x+25 C、75%x-35=95%x-25 D、75%x+35=95%x-25

查看试题解析
8. 下列说法中错误的是（）

A、单项式6abc的次数为3 B、单项式 $- \frac{2 v t}{3}$ 的系数是-2 C、 $\sqrt{6}$ 是无理数 D、xy-2x＋4是二次三项式

查看试题解析
9. 解方程 $\frac{1.5 x}{0.6} - \frac{1.5 - x}{2} = 0.5$ ，以下变形正确的是（）

A、 $\frac{5 x}{2} - \frac{1.5 - x}{2} = 5$ B、 $\frac{5 x}{2} - \frac{15 - 10 x}{2} = 5$ C、 $\frac{5 x}{2} - \frac{15 - 1 x}{20} = 5$ D、 $\frac{5 x}{2} - \frac{3 - 2 x}{4} = 0.5$

查看试题解析
10. 已知某点阵的第①②③个图如图所示，按此规律第（）个点阵图中，点的个数为2022个．

A、1009 B、2018 C、2022 D、2048

查看试题解析

二、填空题

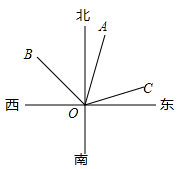
11. 4的平方根是

查看试题解析
12. 计算：35°49＇＋44°26＇＝．

查看试题解析
13. 用代数式表示：x的2倍与y的平方的差．

查看试题解析
14. 若一个角是 $5 3^{∘}$ ，则它的补角是．

查看试题解析
15. 已知4x-y＝0，用含x的代数式来表示y为．

查看试题解析
16. 绝对值小于 $\sqrt{41}$ 的整数有个．

查看试题解析
17. 如图， $O A$ 的方向是北偏东 $15^{\circ}$ ， $O B$ 的方向是西北方向，若 $∠ A O C = ∠ A O B$ ，则 $O C$ 的方向是.

查看试题解析
18. 已知线段AB＝8cm，C是直线AB上的一点AC＝3.2cm，M、N分别是AB、AC的中点，则MN的长等于cm．

查看试题解析
19. 《九章算术》是我国古代数学名著，卷七“盈不足”中有题译文如下：今有人合伙买一只羊，每人出5钱，会差45钱；每人出7钱，会差3钱.问合伙人数、羊价各是多少？设羊价为x钱，所列方程是.

查看试题解析
20. 张师傅晚上出门散步，出门时6点多一点，他看到手表上的分针与时针的夹角恰好为120°，回来时接近7点，他又看了一下手表，发现此时分针与时针再次成120°，则张师傅此次散步的时间是分钟．

查看试题解析

三、解答题

21. 计算：

(1)、-3+12-15

(2)、 $(\frac{2}{3} - \frac{5}{6} + \frac{1}{9}) \times (- 18)$

查看试题解析
22. 解方程：

(1)、8x-3(2x+1)=1

(2)、 $\frac{3 x - 1}{4} - 1 = \frac{5 x - 7}{6}$

查看试题解析
23. 画图并度量，已知点A是直线l上一点，点M、N是直线l外两点．
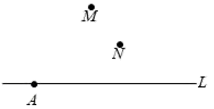
⑴画线段MA，并用刻度尺找出它的中点B；
⑵画直线MN，交直线l于点C，并画出射线CB；
⑶画出点M到直线l的垂线段MH，并量出点M到直线l的距离为多少cm？（精确到0.1cm）

查看试题解析
24. 先化简，再求值：-（a²＋6ab＋9）＋2（a²＋4ab-4.5），其中a＝-2，b＝6．

查看试题解析
25. 如图，直线AE与CD相交于点B，∠DBE＝65°，BF⊥AE，求∠FBD和∠CBF的度数．

查看试题解析
26. 定海白泉镇以皋泄的“晚稻杨梅”闻名，今年“晚稻杨梅”大丰收，社区要把240吨“晚稻杨梅”运往某市的A，B两地．用大、小两种货车共20辆，恰好能一次性运完这批“晚稻杨梅”，已知这两种货车的载重量分别为15吨每辆和10吨每辆．

(1)、这两种货车各有多少辆？

(2)、运往A地的运费为：大车每辆630元，小车每辆420元，运往B地的运费为：大车每辆750元，小车每辆550元，若把20辆货车中的10辆安排前往A地，其余货车前往B地，设前往A地的大车为a辆．
①完成下表空格（用含a的代数式表示）：

A地
B地
大车（辆）
a
小车（辆）
②若总运费为11330元，求a的值．

查看试题解析
27. 已知M、N两点在数轴上所表示的数分别为m，n，且满足 $| m - 11 | + (n + 4)^{2} = 0$ ．

(1)、m= ， n=；

(2)、若点P从N点出发，以每秒1个单位长度的速度向右运动，同时点Q从M点出发，以每秒2个单位长度的速度向左运动，经过多长时间后P、Q两点相距6个单位长度？

(3)、若点A、B为线段M、N上的两点，且NA＝AB＝BM，点P从N点出发，以每秒3个单位长度的速度向左运动，点Q从M点出发，以每秒4个单位长度的速度向右运动，点R从B点出发，以每秒5个单位长度的速度向右运动，P、Q、R同时出发，是否存在常数k，使得 $P Q - k A R$ 的值与它们的运动时间无关，为定值？若存在，请求出k和这个定值；若不存在，请说明理由．

查看试题解析

	A地	B地
大车（辆）	a
小车（辆）