浙江省金华市婺城区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. 图中的蛋糕的形状类似于（）

A、圆 B、球体 C、圆锥体 D、圆柱体

查看试题解析
2. 下列各数中，最小的数是（）

A、-3 B、-2 C、0 D、2

查看试题解析
3. 2021年6月17日，我国的神舟十二号载人飞船搭载着聂海胜、刘伯明、汤洪波三名宇航员成功飞天，共飞行约58940000km.数据58940000用科学记数法表示为（）

A、 $0.5894 \times 1 0^{8}$ B、 $5.894 \times 1 0^{8}$ C、 $5.894 \times 1 0^{7}$ D、 $58.94 \times 1 0^{6}$

查看试题解析
4. 以下代数式中，不属于整式的是（）

A、m B、 $\frac{2}{m}$ C、 $\frac{m}{2}$ D、2

查看试题解析
5. 关于“ $\sqrt{16}$ ”的三种说法：① $\sqrt{16}$ 表示16的平方根；② $\sqrt{16} = 4$ ；③ $\sqrt{16}$ 是无理数．其中正确的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
6. 下列图形中，线段 $P Q$ 能表示点P到直线l的距离的是（）．

A、 B、 C、 D、

查看试题解析
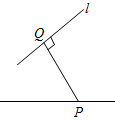7. 图中下列从 $A$ 到 $B$ 的各条路线中最短的路线是（）

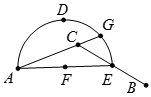A、 $A \to C \to G \to E \to B$ B、 $A \to C \to E \to B$ C、 $A \to D \to G \to E \to B$ D、 $A \to F \to E \to B$

查看试题解析
8. 《算学启蒙》中有一道题，原文是：良马日行二百四十里，驽马日行一百五十里.驽马先行一十二日，问良马几何追及之？译文为：跑的快的马每天走240里，跑的慢的马每天走150里.慢马先走12天，快马几天可以追上慢马？设快马x天可以追上慢马，可列方程（）

A、240x＝150（x+12） B、240（x﹣12）＝150x C、240（x+12）＝150x D、240x＝150（x﹣12）

查看试题解析
9. 如图，已知线段AB=a，线段CD=b，线段CD在线段AB上运动（点C、D始终在线段AB上），在CD的运动中，则图中所有线段的长度和是（）

A、2a+2b B、3a+b C、3a+2b D、随着CD位置的改变而发生变化

查看试题解析
10. 如图，正六边形ABCDEF（每条边都相等）在数轴上的位置如图所示，点A、F对应的数分别为-2和-1，现将正六边形ABCDEF绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点E所对应的数为0，连续翻转2000次后，数轴上1998这个数所对应的点是（）

A、A点 B、D点 C、E点 D、F点

查看试题解析

二、填空题

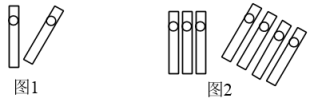
11. —2022的绝对值是.

查看试题解析
12. 若 $2 x^{2} y^{a}$ 与 $3 x^{b} y^{3}$ 是同类项，则 $(- b)^{a}$ = ．

查看试题解析
13. 已知 $∠ α = 20 ° 2 0^{'}$ ，则 $∠ α$ 的补角的度数为= ．

查看试题解析
14. 魏晋时期数学家刘微在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数，图1表示的数值为： $(+ 1) + (- 1) = 0$ ，则可推算图2表示的数值是．（请直接写出最后的结果）

查看试题解析
15. 如图，点P是长方形ABCD内的点，将线段CD沿射线CP折叠得到线段CD'．若∠BCD'=10°，则∠BCP=°．

查看试题解析
16. 在求两位数的平方时，可以用“列竖式”的方法进行速算，求解过程如图1所示．

(1)、仿照图1，在图2中补全67²的“竖式”，空格处的两个数从左到右依次为．

(2)、仿照图1，用“列竖式”的方法计算一个两位数的平方，部分过程如图3所示，若这个两位数的十位数字为a，则这个两位数为（用含a的代数式表示）．

查看试题解析

三、解答题

17. 计算： $- 1^{2} + \sqrt[3]{- 27} + | - 3 | \div \frac{1}{3} - (- 2017)$

查看试题解析
18. 解下列方程：

(1)、x-4=3x+6；

(2)、x- $\frac{x + 2}{3}$ =1．

查看试题解析
19. 已知线段AB与点C的位置如图所示，按下列要求画出图形.

(1)、作射线CB；

(2)、作直线AC；

(3)、①延长AB至点E，使得AE=3AB；
②在①的条件下，若AB=2cm，则BE= ▲ cm．

查看试题解析
20. 设A= $3 a x^{3} - b x$ ， B= $- a x^{3} - 2 b x + 8$ ．

(1)、求A+B；

(2)、当 $x$ ＝－1，A+B=10时，求代数式 $2 a - 3 b$ 的值．

查看试题解析
21. 如图，自行车每节链条的长度为2.3cm，交叉重叠部分的圆的直径为0.7cm．

(1)、2节链条长cm，5节链条长cm，n节链条长cm；

(2)、如果一辆自行车的链条的总长度为99.9cm，求这辆自行车上有几节链条？

查看试题解析
22. 为更好地营造“多读书、读好书、好读书”的书香校园氛围，学校图书馆向出版商邮购某系列图书．相关的书价折扣、邮费如下表所示．（注：总费用=总书价+总邮费）
数量
折扣
邮费
不超过10本
九折
7元
超过10本
八五折
优惠后总书价的10%

(1)、已知书的单价为15元，需购书30本.
①若采用分次邮购，每次10本，共需总费用为元；
②若采用一次性邮购，共需费用为元.

(2)、已知图书馆需购书的总数是10的整数倍，且超过10本．图书馆负责人发现分次邮购所需费用与一次性邮购所需费用相同，求书的单价是多少元？

查看试题解析
23. 对于平面内的两点M、N，若直线MN上存在点P，使得MP= $\frac{1}{2}$ NP成立，则称
点P为点M、N的“和谐点”，但点P不是点N、M的“和谐点”.

(1)、如图1，点A、B在直线l上，点C、D是线段AB的三等分点，则是点A、B的“和谐点”（填“点C或“点D”）；

(2)、如图2，已知点E、F、G在数轴上，点E表示数－2，点F表示数1，且点F是点E、G的“和谐点”，求点G表示的数；

(3)、如图3，数轴上的点P表示数5，点M从原点O出发，以每秒3个单位的速度向左运动，点N从点P出发，以每秒10个单位的速度向左运动，点M、N同时出发.在M、N、P三点中，若点M是另两个点的“和谐点”，则OM=.

查看试题解析
24. 如图，直线AB与EF相交于点O，∠AOE=60°，射线OC平分∠BOE．

(1)、求∠COF的度数；

(2)、将射线OC以每秒2°的速度绕点O顺时针旋转，同时直线EF以每秒6°的速度绕点O顺时针旋转，设运动时间为t秒（0＜t≤60)．
①当射线OE与射线OC重合时，求∠AOE的度数；
②旋转过程中，若直线EF平分∠BOC或平分∠AOC，求t的值.

查看试题解析

数量	折扣	邮费
不超过10本	九折	7元
超过10本	八五折	优惠后总书价的10%