2022年秋季浙教版数学九年级上册期末复习检测A
试卷更新日期:2022-11-09 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 四张不透明的卡片,正面标有数字分别是﹣2,3,﹣10,6,除正面数字不同外,其余都相同,将它们背面朝上洗匀后放在桌面上,从中随机抽取一张卡片,则这张卡片正面的数字是﹣10的概率是( )A、 B、 C、 D、12. 已知 , ,若 ,则 ( )A、4 B、6 C、8 D、163. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 已知抛物线 的对称轴在 轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则 的值是( )A、-5或2 B、-5 C、2 D、-25. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )
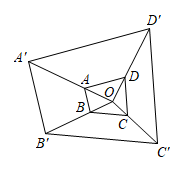 A、4 B、6 C、16 D、186. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )
A、4 B、6 C、16 D、186. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )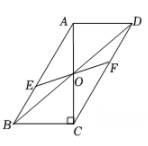 A、
A、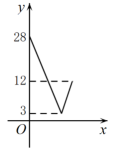 B、
B、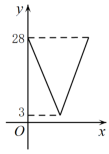 C、
C、 D、
D、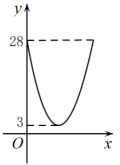 7. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
7. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )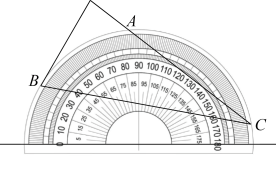 A、28° B、30° C、36° D、56°8. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )
A、28° B、30° C、36° D、56°8. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )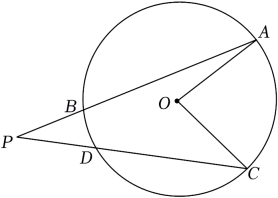 A、30° B、25° C、20° D、10°9. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )
A、30° B、25° C、20° D、10°9. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )①EC⊥AG;②△OBP∽△CAP;③OB平分∠CBG;④∠AOD=45°;
 A、①③ B、①②③ C、②③ D、①②④10. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为 , 且经过点(-1,0).下列结论:①3a+b=0;②若点 , (3,y2)是抛物线上的两点,则y1<y2;③10b-3c=0;④若y≤c,则0≤x≤3.其中正确的有( )
A、①③ B、①②③ C、②③ D、①②④10. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为 , 且经过点(-1,0).下列结论:①3a+b=0;②若点 , (3,y2)是抛物线上的两点,则y1<y2;③10b-3c=0;④若y≤c,则0≤x≤3.其中正确的有( )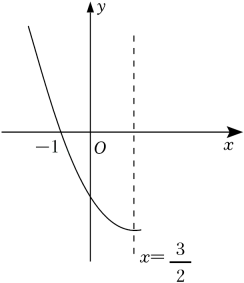 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共18分)
-
11. 如图,在平面直角坐标系中,与位似,位似中心是坐标原点O.若点 , 点 , 则与周长的比值是 .
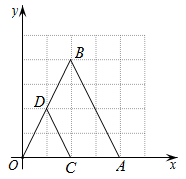 12. 在北京冬奥会自由式滑雪大跳台比赛中,我国选手谷爱凌的精彩表现让人叹为观止,已知谷爱凌从2m高的跳台滑出后的运动路线是一条抛物线,设她与跳台边缘的水平距离为xm,与跳台底部所在水平面的竖直高度为ym,y与x的函数关系式为y=x2+x+2(0≤x≤20.5),当她与跳台边缘的水平距离为m时,竖直高度达到最大值.
12. 在北京冬奥会自由式滑雪大跳台比赛中,我国选手谷爱凌的精彩表现让人叹为观止,已知谷爱凌从2m高的跳台滑出后的运动路线是一条抛物线,设她与跳台边缘的水平距离为xm,与跳台底部所在水平面的竖直高度为ym,y与x的函数关系式为y=x2+x+2(0≤x≤20.5),当她与跳台边缘的水平距离为m时,竖直高度达到最大值.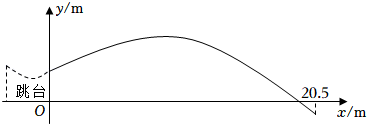 13. 如图,等边三角形ABC内接于⊙O,BC=2 , 则图中阴影部分的面积是 .
13. 如图,等边三角形ABC内接于⊙O,BC=2 , 则图中阴影部分的面积是 .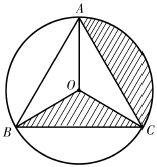 14. 如图,在中, , 点P为边上任意一点,连接 , 以 , 为邻边作平行四边形 , 连接 , 则长度的最小值为.
14. 如图,在中, , 点P为边上任意一点,连接 , 以 , 为邻边作平行四边形 , 连接 , 则长度的最小值为.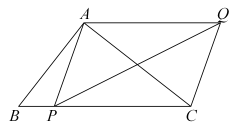 15. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).
15. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).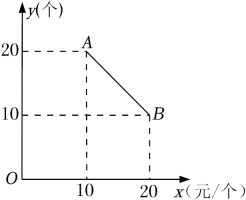 16. 如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,若BF:FD=3:1,AB+BE=3 , 则△ABC的周长为 .
16. 如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,若BF:FD=3:1,AB+BE=3 , 则△ABC的周长为 .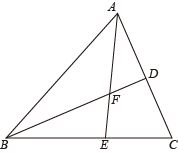
三、解答题(共8题,共72分)
-
17. 教育部在《大中小学劳动教育指导纲要(试行)》中明确要求:初中生每周课外生活和家庭生活中,劳动时间不少于3小时.某走读制初级中学为了解学生劳动时间的情况,对学生进行了随机抽样调查,并将调查结果制成不完整的统计图表,如图:
平均每周劳动时间的频数统计表
劳动时间小时
频数
t<3
9
3≤t<4
a
4≤t<5
66
t≥5
15

请根据图表信息,回答下列问题.
(1)、参加此次调查的总人数是人,频数统计表中a=;(2)、在扇形统计图中,D组所在扇形的圆心角度数是°;(3)、该校准备开展以“劳动美”为主题的教育活动,要从报名的2男2女中随机挑选2人在活动中分享劳动心得,请用树状图或列表法求恰好抽到一名男生和一名女生的概率.18. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证: (1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ19. 如图,正方形内接于 , 点E为的中点,连接交于点F,延长交于点G,连接.
(1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ19. 如图,正方形内接于 , 点E为的中点,连接交于点F,延长交于点G,连接.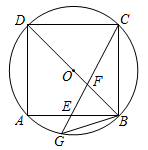 (1)、求证:;(2)、若.求和的长.20. 如图,四边形为菱形,点E在的延长线上, .
(1)、求证:;(2)、若.求和的长.20. 如图,四边形为菱形,点E在的延长线上, . (1)、求证:;(2)、当时,求的长.21. 如图,△ABC内接于⊙O,交⊙O于点D,交BC于点E,交⊙O于点F,连接AF,CF.
(1)、求证:;(2)、当时,求的长.21. 如图,△ABC内接于⊙O,交⊙O于点D,交BC于点E,交⊙O于点F,连接AF,CF.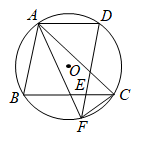 (1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).22. 丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:
(1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).22. 丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:销售单价x(元/件)
…
35
40
45
…
每天销售数量y(件)
…
90
80
70
…
(1)、直接写出y与x的函数关系式;(2)、若每天销售所得利润为1200元,那么销售单价应定为多少元?(3)、当销售单价为多少元时,每天获利最大?最大利润是多少元?23. 如图,四边形ABCD内接于 , 对角线AC,BD相交于点E,点F在边AD上,连接EF.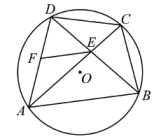 (1)、求证:;(2)、当时,则;;.(直接将结果填写在相应的横线上)(3)、①记四边形ABCD,的面积依次为 , 若满足 , 试判断,的形状,并说明理由.
(1)、求证:;(2)、当时,则;;.(直接将结果填写在相应的横线上)(3)、①记四边形ABCD,的面积依次为 , 若满足 , 试判断,的形状,并说明理由.②当 , 时,试用含m,n,p的式子表示.
24. 如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.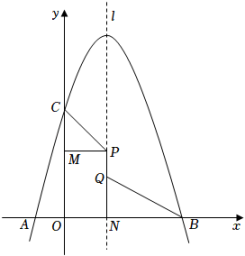 (1)、直接写出A,B,C三点的坐标;(2)、求CP+PQ+QB的最小值;(3)、过点P作PM⊥y轴于点M,当CPM和QBN相似时,求点Q的坐标.
(1)、直接写出A,B,C三点的坐标;(2)、求CP+PQ+QB的最小值;(3)、过点P作PM⊥y轴于点M,当CPM和QBN相似时,求点Q的坐标.