人教版数学七年级上找规律练习合集-------数轴线段相关2

试卷更新日期：2022-11-09 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第一次将点A向左移动3个单位长度到达点A₁ ，第二次将点A向右移动6个单位长度到达点A₂ ，第三次将点A₂向左移动9个单位长度到达点A₃ ，按照这种移动规律移动下去，第n次移动到点A_n ，如果点A_n与原点的距离不小于20，那么n的最小值是（　　）

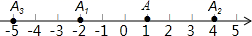A、12 B、13 C、14 D、15

查看试题解析
2. 如图，数轴上两定点A、B对应的数分别为－18和14，现在有甲、乙两只电子蚂蚁分别从A、B同时出发，沿着数轴爬行，速度分别为每秒1.5个单位和1.7个单位，它们第一次相向爬行1秒，第二次反向爬行2秒，第三次相向爬行3秒，第四次反向爬行4秒，第五次相向爬行5秒，……，按如此规律，则它们第一次相遇所需的时间为（）

A、55秒 B、190秒 C、200秒 D、210秒

查看试题解析
3. 如图，2条直线相交有1个交点，3条直线相交最多有3个交点，4条直线相交最多有6个交点…按这样的规律若n条直线相交交点最多有28个，则此时n的值为（）

A、18 B、10 C、8 D、7

查看试题解析

二、填空题

4. 数轴上 $O$ ， $A$ 两点的距离为 $9$ ，一动点P从点A出发，按以下规律跳动：第1次跳动到 $A O$ 的中点 $A_{1}$ 处，第2次从 $A_{1}$ 点跳动到 $A_{1} O$ 的中点 $A_{2}$ 处，第3次从 $A_{2} O$ 点跳动到的中点 $A_{3}$ 处、按照这样的规律继续跳动到点 $A_{4}$ ， $A_{5}$ ， $A_{6}$ ，…， $A_{n}$ （ $n \geq 3$ ， $n$ 是整数）处，那么线段 $A_{n} A$ 的长度为.

查看试题解析
5. 一跳蚤在一直线上从O点开始，第一次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依次规律跳下去，当它跳第2021次落下时，落点处离O点的距离是个单位.

查看试题解析
6. 先阅读下列材料，再解决问题：
学习数轴之后，有同学发现在数轴上到两点之间距离相等的点，可以用表示这两点表示的数来确定.如：(1)到表示数4和数10距离相等的点表示的数是7，有这样的关系7= $\frac{1}{2}$ (4+10)； (2)到表示数-3和数-7距离相等的点表示的数是-5，有这样的关系-5= $\frac{1}{2} [(- 3) + (- 7)]$ .

解决问题：根据上述规律完成下列各题：

(1)、到表示数50和数150距离相等的点表示的数是

(2)、到表示数 $\frac{2}{3}$ 和数 $- \frac{5}{8}$ 距离相等的点表示的数是

(3)、到表示数-12和数-26距离相等的点表示的数是

(4)、到表示数a和数b距离相等的点表示的数是

查看试题解析
7. 如图，数轴上两定点A、B对应的数分别为-18和14，现在有甲、乙两只电子蚂蚁分别从A、B同时出发，沿着数轴爬行，速度分别为每秒1.5个单位和1.7个单位，它们第一次相向爬行1秒，第二次反向爬行2秒，第三次相向爬行3秒，第四次反向爬行4秒，第五次相向爬行5秒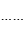，，按如此规律，则它们第一次相遇所需的时间为s.

查看试题解析
8. 如图，在数轴上， $A_{1}$ ， $P$ 两点表示的数分别是1，2，若 $A_{1}$ 与 $A_{2}$ 到点 $O$ 的距离相等， $A_{2}$ 与 $A_{3}$ 到点 $P$ 的距离相等， $A_{3}$ 与 $A_{4}$ 到点 $O$ 的距离相等， $A_{4}$ 与 $A_{5}$ 到点 $P$ 的距离相等……依此规律，则点 $A_{10}$ 表示的数是.

查看试题解析
9. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第一次将点A向左移动3个单位长度到达点A₁ ，第2次将点A₁向右平移6个单位长度到达点A₂ ，第3次将点A₂向左移动9个单位长度到达点A₃…则第6次移动到点A₆时，点A₆在数轴上对应的实数是；按照这种规律移动下去，至少移动次后该点到原点的距离不小于41．

查看试题解析

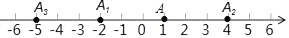
三、解答题

10. ① 如图（1），直线l上有2个点，则图中有2条可用图中字母表示的射线：A₁A₂、A₂A₁ ，有1条线段：A₁A₂；
② 如图（2），直线l上有3个点，则图中有几条可用图中字母表示的射线，有几条线段，并分别用图中字母表示出来；

③ 如图（3），直线l上有n个点，则图中有多少条可用图中字母表示的射线，有多少条线段，分别用含n的代数式表示出来；

④ 应用（3）中发现的规律解决问题：某校七年级共有8个班进行足球比赛，准备进行循环赛（即每两队之间赛一场），预计全部赛完共需多少场比赛？

查看试题解析
11.
（1）已知：如图，点C在线段AB上，线段AC=15，BC=5，点M、N分别是AC、BC的中点，求MN的长度．
（2）根据（1）的计算过程与结果，设AC+BC=a，其它条件不变，你能猜出MN的长度吗？请用简洁的语言表达你发现的规律．
（3）若把（1）中的“点C在线段AB上”改为“点C在直线AB上”，其它条件不变，结论又如何？请说明你的理由．

查看试题解析

四、综合题

12. （背景知识）数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律：若数轴上点A、点B表示的数分别为a、b，则A，B两点之间的距离AB= $| a - b |$ ，线段AB的中点表示的数为 $\frac{a + b}{2}$ .如图，数轴上点A表示的数为 $- 2$ ，点B表示的数为8.
（综合运用）

(1)、填空：A，B两点间的距离AB= ，线段AB的中点表示的数为；

(2)、若M为该数轴上的一点，且满足MA+MB=12，求点M所表示的数；

(3)、若点P从点A出发，以每秒1个单位长度的速度沿数轴向终点B匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动，Q到达A点后，再立即以同样的速度返回B点，当点P到达终点后，P、Q两点都停止运动，设运动时间为t秒（ $t > 0$ ）.当t为何值时，P，Q两点间距离为4.

查看试题解析
13. 综合探究
【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：如图①，若数轴上点A、点B表示的数分别为a，b（b＞a），则线段AB的长（点A到点B的距离）可表示为b－a．请用上面材料中的知识解答下面的问题：
【问题情境】如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达点A，再向右移动3个单位长度到达点B，然后再向右移动5个单位长度到达点C．

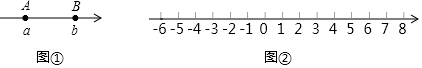(1)、【问题探究】请在图②中表示出A、B、C三点的位置；

(2)、【问题探究】若点P从点A出发，以每秒1个单位长度的速度沿数轴向左匀速运动，同时点M、N从点B、点C分别以每秒2个单位长度、每秒3个单位长度速度沿数轴向右匀速运动．设移动时间为t秒(t＞0)．
①A，B两点间的距离AB= ▲ ， AC= ▲ ；
②若点D、E分别是线段AB，BC的中点，求线段DE的长；
③用含t的代数式表示：t秒时，点P表示的数为 ▲ ，点M表示的数为 ▲ ，点N表示的数为 ▲ ；
④试探究在移动的过程中，3PN－4PM的值是否随着时间t的变化而变化？若变化说明理由；若不变，请求其值．

查看试题解析
14. （背景知识）数轴是初中数学学习的一个重要工具，利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律，例如：若数轴上点 $A$ ， $B$ 分别对应数 $a$ ， $b$ .则 $A$ ， $B$ 两点之间的距离为 $A B = | a - b |$ ，线段 $A B$ 的中点表示的数为 $\frac{a + b}{2}$ .
（问题情境）如图，数轴上点 $A$ ， $B$ 分别对应数 $a$ ， $b$ .其中 $a < 0$ ， $b > 0$ .

（综合运用）

(1)、当 $a = - 8$ ， $b = 2$ 时，线段 $A B$ 的中点对应的数是；

(2)、若该数轴上另有一点 $N$ 对应着数 $n$ .
①在（1）的条件下，若点 $N$ 在点 $A$ ， $B$ 之间，且满足 $N A - N B = 8 N O$ ，则数 $n$ 是；

②当 $n = - 3$ ， $a < - 3$ ，且 $A N = 4 B N$ 时，求代数式 $a + 4 b + 16$ 的值；

③当 $b = 3$ ，且 $B N = 3 A N$ 时，小林演算发现代数式 $4 n - 3 a$ 是一个定值.

老师点评：你的演算发现还不完整！

请通过演算解释：为什么“小林的演算发现”是不完整的？

查看试题解析
15. 如图，数轴上A ， B两点对应的数分别-4，8．有一动点P从点A出发第一次向左运动1个单位长度；然后在新的位置第二次运动，向右运动2个单位长度；在此位置第三次运动，向左运动3个单位长度，…按照如此规律不断地左右运动

(1)、当运动到第2018次时，求点P所对应的有理数．

(2)、点P会不会在某次运动时恰好到达某一个位置，使点P到点B的距离是点P到点A的距离的3倍？若可能请求出此时点P的位置，若不可能请说明理由．

查看试题解析
16. 小明在一条直线上选了若干个点，通过数线段的条数，发现其中蕴含了一定的规律，下边是他的探究过程及联想到的一些相关实际问题.

(1)、一条直线上有2个点，线段共有1条；一条直线上有3个点，线段共有1+2=3条；一条直线上有4个点，线段共有1+2+3=6条…一条直线上有10个点，线段共有
条.

(2)、总结规律：一条直线上有n个点，线段共有条.

(3)、拓展探究：具有公共端点的两条射线OA、OB形成1个角∠AOB（∠AOB＜180°）；在∠AOB内部再加一条射线OC，此时具有公共端点的三条射线OA、OB、OC共形成3个角；以此类推，具有公共端点的n条射线OA、OB、OC…共形成个角

(4)、解决问题：曲沃县某学校九年级1班有45名学生毕业留影时，全体同学拍1张集体照，每2名学生拍1张两人照，共拍了多少张照片？如果照片上的每位同学都需要1张照片留作纪念，又应该冲印多少张纸质照片？

查看试题解析
17. （背景知识）
数轴是初中数学的一个重要工具．利用数轴可以将数与形完美的结合．研究数轴我们发现了许多重要的规律：数轴上A点、B点表示的数为a、b，则A，B两点之间的距离AB＝|a﹣b|，若a＞b，则可简化为AB＝a﹣b；线段AB的中点M表示的数为 $\frac{a + b}{2}$ ．

（问题情境）

已知数轴上有A、B两点，分别表示的数为﹣10，8，点A以每秒3个单位的速度沿数轴向右匀速运动，点B以每秒4个单位向左匀速运动．设运动时间为t秒（t＞0）．

(1)、（综合运用）
运动开始前，线段AB的中点M所表示的数；点A运动t秒后所在位置的点表示的数为．（用含t的式子表示）

(2)、若A、B两点按上述方式运动，A、B两点经过多少秒会相距4个单位长度？

(3)、若A，B两点按上述方式运动，线段AB的中点M能否与表示﹣2的点重合？若能，求出运动时间，并直接写出中点M的运动方向和运动速度；若不能，请说明理由．（当A，B两点重合，则中点M也与A，B两点重合）

(4)、若点A运动到原点处调转方向，沿数轴向左按原来的速度运动，点B的运动方向和速度不变，则点B出发几秒时，与点A相距10个单位长度（t＞ $\frac{10}{3}$ ）？

查看试题解析