人教版数学七年级上找规律练习合集-------图形数字相关1

试卷更新日期：2022-11-09 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，在纸面所在的平面内，一只电子蚂蚁从数轴上表示原点的位置O点出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其移动路线如图所示，第1次移动到A₁ ，第2次移动到A₂ ，第3次移动到A₃ ， ……，第n次移动到A_n ，则△OA₂A₂₀₂₂的面积是（）

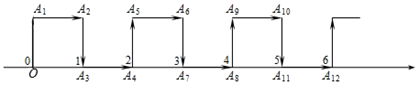A、505 B、 $\frac{2021}{2}$ C、 $\frac{1011}{2}$ D、1011

查看试题解析
2. 填在下面三个田字格内的数有相同的规律，根据此规律，C 的值是（）

A、76 B、82 C、86 D、108

查看试题解析
3. 观察下列算式：3¹=3 3²=9 3³=27 3⁴=81 3⁵=243 3⁶=729…通过观察，用你所发现的规律得出3²⁰¹⁶的末位数是（）

A、1 B、3 C、7 D、9

查看试题解析
4. 将正整数按如图所示的位置顺序排列：
根据排列规律，则2015应在（　　）

A、A处 B、B处 C、C处 D、D处

查看试题解析
5. 已知：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，…，那么2²⁰²¹的个位数字是（）

A、2 B、4 C、6 D、8

查看试题解析
6. 如图所示，圆的周长为4个单位长度，在圆周的四等分点处标上字母A，B，C，D，先将圆周上的字母A对应的点与数轴上的原点重合，再将圆沿着数轴向右滚动，那么数轴上的2022所对应的点与圆周上字母（）所对应的点重合．

A、A B、B C、C D、D

查看试题解析

二、填空题

7. 用黑白两种颜色的正六边形地砖按如图所示的规律拼成若干图案：
(1)第 4 个图中白砖有块；(2)第 n 个图中白砖有块

第1个第2个第3个

查看试题解析
8. 动脑筋、找规律，李老师给小明出了下面的一道题，请根据数字排列的规律，探索下列问题：

(1)、在A处的数是正数还是负数；

(2)、负数排在A，B，C，D中的位置？

(3)、第2017个数是正数还是负数，排在对应于A，B，C，D中的位置？

查看试题解析
9. 从图①中找出规律，并按规律从图②中找出 $a$ ， $b$ ， $c$ 的值，计算 $a + b - c$ 的值是．

查看试题解析
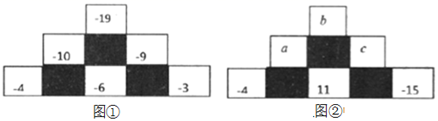10. 如图，数轴上的O点为原点，A点表示的数为﹣2，动点P从O点出发，按以下规律跳动：第1次从O点跳动到OA的中点A₁处，第2次从A₁点跳动到A₁A的中点A₂处，第3次从A₂点跳动到A₂A的中点A₃处，…，第n次从An_﹣₁点跳动到An_﹣₁A的中点An处，按照这样的规律继续跳动到点A₄ ， A₅ ， A₆ ， …，An（n≥3，n是整数）处，那么An点所表示的数为.

查看试题解析
11. 观察下面两行数：
-2，4，-8，16，-32，64，…

1，7，-5，19，-29，67，…根据你发现的规律，取每行数的第9个数，它们的和等于.

查看试题解析
12. 如图是一组有规律的图案，图案1是由4个组成的，图案2是由7个组成的，依此，第n个图案是由个组成的.

查看试题解析
13. 下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有1颗棋子，第②个图形一共有6颗棋子，第③个图形一共有16颗棋子，……，则第⑩个图形中棋子的颗数为.

查看试题解析
14. 如图所示，将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为a₁ ，第2幅图形中“●”的个数为a₂ ，第3幅图形中“●”的个数为a₃ ， …，以此类推，则 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + \cdot \cdot \cdot + \frac{1}{a_{8}}$ 的值为

查看试题解析
15. 找出下列各图形中数的规律，依此，a的值为．

查看试题解析
16. 如图，观察由棱长为1的小立方体摆成的图形，寻找规律：如图①中：共有1个小立方体，其中1个看得见，0个看不见；如图②中：共有8个小立方体，其中7个看得见，1个看不见；如图③中：共有27个小立方体，其中19个看得见，8个看不见；…，则第⑥个图中，看得见的小立方体有个.

查看试题解析
17. 平移小菱形◇可以得到美丽的“中国结”图案，下面四个图案是由◇平移后得到的类似“中国结”的图案，按图中规律，第20个图案中，小菱形的个数是．

查看试题解析
18. 如图①是一块瓷砖的图案，用这种瓷砖铺设地面，如果铺设成如图②的图案，其中完整的圆一共有5个，如果铺设成如图③的图案，其中完整的圆一共有13个，如果铺设成如图④的图案，其中完整的圆一共有25个，以此规律下去，第10个图中，完整的圆一共有个.

查看试题解析
19. 按下图规律，在第四个方框内填入的数应为．

查看试题解析
20. 如图是一根起点为1的数轴，现有同学将它弯折，弯折后虚线上由左至右第1个数是1，第2个数是13，第3个数是41，…，依此规律，第5个数是.

查看试题解析
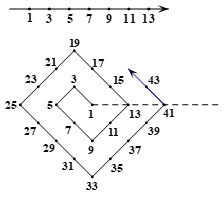21. 如图，用相同的小正方形按照某种规律进行摆放，则第6个图形中小正方形的个数是，第n（n为正整数）个图形中小正方形的个数是（用含n的代数式表示）．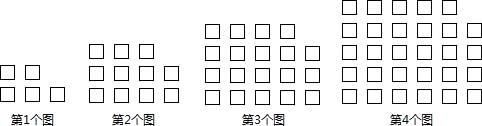

查看试题解析

三、解答题

22. 将2020减去它的 $\frac{1}{2}$ ，再减去余下的 $\frac{1}{3}$ ，再减去余下的 $\frac{1}{4}$ ，再减去余下的 $\frac{1}{5}$ ……以此类推，直到最后减去余下的 $\frac{1}{2020}$ ，最后的得数是多少？

查看试题解析

四、综合题

23. 观察下列算式的规律：
$1 - \frac{1}{3} = \frac{2}{1 \times 3} ， \frac{1}{3} - \frac{1}{5} = \frac{2}{3 \times 5} ， \frac{1}{5} - \frac{1}{7} = \frac{2}{5 \times 7}$ ，….

请用上述等式反映的规律解答下列问题：

(1)、第n个算式为；

(2)、计算 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{19 \times 21}$ .

查看试题解析
24. 现用棱长为1cm的若干小正方体，按如图所示的规律在地上搭建若干个几何体．图中每个几何体自上而下分别叫第一层，第二层…第n层（n为正整数），其中第一层摆放一个小正方体，第二层摆放4个小正方体，第三层摆放9个小正方体…，依次按此规律继续摆放．

(1)、求搭建第4个几何体需要的小正方体个数：

(2)、为了美观，若将每个几何体的所有露出部分（不包含底面）都喷涂油漆，已知喷涂1cm²需要油漆0.3克．
①求喷涂第4个几何体需要油漆多少克？
②求喷涂第n个几何体需要油漆多少克？（用含n的代数式表示）

查看试题解析
25. 小丽在用等长的木棒设计图案，她先用 $8$ 根木棒摆成图案①，再按图案①的个数逐渐增加 $1$ 的规律拼成下图中的图案②和图案③.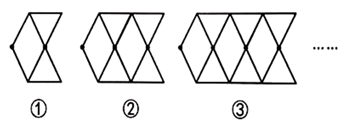

(1)、她在摆第 $5$ 个图案时，用了多少根木棒？

(2)、请你帮她用含 $n$ 的代数式表示第 $n$ 个图案所需木棒的根数.

(3)、如果要摆出第 $50$ 个图案，所需木棒的根数是多少？

查看试题解析
26. 探索规律，观察下面由※组成的图案和算式，解答问题：

1+3=4=2²

1+3+5=9=3²

1+3+5+7=16=4²

1+3+5+7+9=25=5²

(1)、请猜想1+3+5+7+9+…+19= ；

(2)、请猜想1+3+5+7+9+…+（2n－1）=；

查看试题解析
27. 如图所示，将类似于下面的图形称做平面图，其顶点数、边数与区域数之间存在某种关系．观察各图和表中对应的部分数值．探究规律并作答．
图
图（1）
图（2）
图（3）
图（4）
图（5）
顶点数 $V$
4
5
6
8
区域数 $F$
3
4
5
6
边数 $E$
6
8
9
15

(1)、数一数每个图中的顶点数，边数，这些边围出的区域数，完成上面的表格；

(2)、根据表中数值，猜想平面图的顶点数、边数、区域数之间的关系，直接写出你的结论；

(3)、如果一个平面图有20个顶点和11个区域，则这个平面图的边数为．

查看试题解析
28. 为给同学们创造更好的读书条件，学校准备新建一个长度为L的读书长廊，并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起，按如图所示的规律拼成图案铺满长廊，已知每个小正方形地面砖的边长均为0.6m．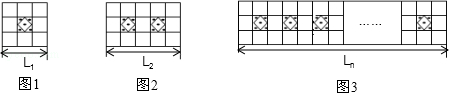

(1)、按图示规律，第一图案的长度L₁=m；第二个图案的长度L₂=m．

(2)、请用代数式表示带有花纹的地面砖块数n与走廊的长度L_n之间的关系．

(3)、当走廊的长度L为36.6m时，请计算出所需带有花纹图案的瓷砖的块数．

查看试题解析
29. 认真观察，寻找规律
第1个算式： $\frac{1}{1 \times 2} -$ $\frac{1}{2 \times 3}$ $= \frac{2}{6}$ ；

第2个算式： $\frac{1}{2 \times 3} -$ $\frac{1}{3 \times 4}$ $= \frac{2}{24}$

第3个算式： $\frac{1}{3 \times 4} -$ $\frac{1}{4 \times 5}$ $= \frac{2}{60}$ ；

第4个算式： $\frac{1}{4 \times 5} -$ $\frac{1}{5 \times 6}$ $= \frac{2}{120}$

用你发现的规律解答问题：

(1)、第n个算式为：；

(2)、计算： $\frac{1}{3}$ + $\frac{1}{12}$ + $\frac{1}{30}$ + $\frac{1}{60}$ ；

(3)、若 $\frac{1}{1 \times 2 \times 3} +$ $\frac{1}{2 \times 3 \times 4} +$ $\frac{1}{3 \times 4 \times 5} + . . . + \frac{1}{n (n + 1) (n + 2)} = \frac{11}{45}$ ，求 n 的值.

查看试题解析
30. 小明是个爱动脑筋的同学，在发现教材中的用方框在月历中移动的规律后，突发奇想，将连续的偶数2，4，6，8，…，排成如表，并用一个十字形框架框住其中的五个数，请你仔细观察十字形框架中的数字的规律，并回答下列问题：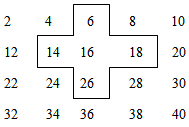

(1)、设中间的数为x ，用代数式表示十字框中的五个数的和；

(2)、若将十字框上下左右移动，可框住另外的五个数，其他五个数的和能等于2016吗？如能，写出这五个数，如不能，说明理由．

查看试题解析
31. 探索规律，观察下面算式，解答问题：
$1 + 3 = 4 = 2^{2}$

$1 + 3 + 5 = 9 = 3^{2}$

$1 + 3 + 5 + 7 = 16 = 4^{2}$

$1 + 3 + 5 + 7 + 9 = 25 = 5^{2}$

……

(1)、填空： $1 + 3 + 5 + 7 + 9 + \cdot \cdot \cdot + 19 =$ ； $1 + 3 + 5 + 7 + 9 + \cdot \cdot \cdot + (2 n - 1) =$ ．

(2)、利用以上规律计算： $49 + 51 + \cdot \cdot \cdot + 97 + 99$ ．

查看试题解析
32. 把具有某种规律的一列数：1，－2，3，－4，5，－6，...，排列成下面的阵形：
........

探索下列事件：

(1)、第10行的第1个数是什么数？

(2)、数字2019前面是负号还是正号?在第几行?第几列?

查看试题解析

图	图（1）	图（2）	图（3）	图（4）	图（5）
顶点数 $V$	4	5	6	8
区域数 $F$	3	4		5	6
边数 $E$	6	8	9		15